線性代數課程思政教學設計

基金項目：國家自然科學基金項目“幾何知識的語義表示與智能化管理方法研究”（61702025）；中國高等教育學會重點項目“基于教育數學思想培養大學數學教師”（22SX0201）；北京航空航天大學一流本科課程立項項目“工科高等代數”（無編號）

作者簡介：陳肖宇（1982-），男，漢族，遼寧沈陽人，博士，講師，碩士研究生導師。研究方向為數學知識管理和教育數學。

DOI：10.19980/j.CN23-1593/G4.2024.19.041

摘? 要：以矩陣求冪問題為例，闡述在線性代數教學中的課程思政設計思路。通過分析教學對象的特點，從知識傳授、能力培養和價值塑造三個方面提出教學目標，并以實際案例為切入點，將學生求知欲的培養、科學思維的鍛煉和報國情懷的激發等思政元素融入教學過程中，達到提升課程教學效果和立德樹人的教學目標。

關鍵詞：線性代數；課程思政；教學設計；矩陣相似；對角化

中圖分類號：G641? ? ? 文獻標志碼：A? ? ? ? ? 文章編號：2096-000X（2024）19-0173-04

Abstract： Taking the problem of computing powers of matrices as an example， this paper elaborates design idea of ideological and political education in teaching Linear Algebra. Through student analysis， we propose teaching objectives from three aspects of knowledge imparting， ability cultivation， and value shaping. Taking practical cases as the starting point， ideological and political elements such as cultivating students' thirst for knowledge， exercising scientific thinking， and inspiring a sense of patriotism are integrated into the teaching process， in order to achieve the goals of improving the effectiveness of the course and cultivating students' moral character.

Keywords： Linear Algebra; ideological education; teaching design; similar matrices; diagonalization

線性代數屬于大學非數學類專業核心必修課，不僅是學生必須掌握的數學基礎，而且在現代科學技術的各個領域有著十分廣泛的應用，這為課程思政元素的挖掘、尋找切入點以及轉變教學方式提供了平臺。線性代數課程知識體系中蘊含著豐富的思政元素[1-5]，而由于線性代數概念抽象難懂，學生理解起來并不容易。從案例出發引出所講解的知識點，一方面可以啟發學生思考如何應用所學知識解決實際問題，幫助學生更好地理解知識要點，使學生體會到數學并不是冰冷的符號游戲，進而提升課程的教學質量和效果[6-7]；另一方面，可以在案例教學過程中將價值塑造融入知識傳授和能力培養，實現立德樹人的教學目標。本文以實際應用中廣泛出現的矩陣求冪問題為例，展示如何在教學中通過案例融入課程思政內容。

一? 案例教學設計

（一）? 教學對象分析

本課程是面向大一本科生的公共基礎課，影響力大，覆蓋面廣，在課程中開展思政教學至關重要。學生處于從高中到大學的過渡階段，學習方式需要改變以適應大學要求，因此應該從簡單的案例出發，以激發學生學習興趣為主，通過合理的引導和分析，一步一步地解決問題，歸納出一般方法和步驟，使學生主動思考解決更復雜的案例。

（二）? 教學目標

1）知識傳授：理解矩陣相似對角化的概念以及方陣特征值和特征向量在矩陣相似對角化中所承擔的角色，掌握矩陣的相似對角化方法和判別條件，理解矩陣相似對角化與矩陣求冪之間的關系，了解很多實際問題都可以轉化為矩陣求冪問題，進而利用矩陣相似對角化解決。

2）能力培養：培養思維能力，能夠對問題進行觀察和分析，培養學生“從特殊到一般”的抽象概括的思維方式，鍛煉學生獨立思考的學習習慣與勇于質疑的科學精神；提高學生“從一般到特殊”的實際問題處理能力，能夠應用所學知識去識別、表達、研究和解決生產生活中的具體問題。

3）價值塑造：能用科學的思維研究問題，用數學的方法解決問題，激發學生的愛國情懷和使命擔當，幫助學生塑造正確的世界觀、人生觀、價值觀。

（三）? 設計理念

首先從著名的斐波那契數列出發，在展現數學之美的過程中引入矩陣的相似等教學內容，引導學生利用矩陣相似對角化求解斐波那契數列的通項公式，培養學生科學思維和嚴謹的科學作風；其次，剖析斐波那契數列的通項公式得到黃金分割比，引出華羅庚的優選法和人物事跡，增強學生愛國主義意識；最后，通過拓展案例，鼓勵學生“在學習中研究，在研究中學習”，培養學生解決實際問題的能力和勇于探索的科研精神。

（四）? 教學重點和難點

理解如何應用矩陣方法描述實際問題，掌握矩陣相似對角化的性質和判別條件，能夠根據數學結果解釋實際問題。

二? 案例教學實施

（一）? 知識回顧

復習矩陣特征值和特征向量的定義和計算方法。

（二）? 案例引入：兔子繁殖問題與斐波那契數列

兔子繁殖問題是意大利數學家斐波那契（L. Fibonacci，1175—1250年）在其所著的《算盤書》（1202年）中收錄的一個民間數學問題，敘述如下：設初生的兔子一個月以后成熟，而一對成熟的兔子每月會生一對兔子。假設每次生的一對兔子都是一雄一雌，且所有的兔子都不病不死，那么由一對初生兔子開始，到第12個月總共有多少對兔子[8]？對于這樣一個問題，按照月數從初始第1個月開始得到兔子對數依次是：1，1，2，3，5，8，13，21，34，55，89，144。然而若求第100個月兔子總對數，計算就十分繁瑣，這就需要找到其中的規律。依題意，第n個月兔子總對數fn應滿足如下遞推公式

。

因該數列是斐波那契發現的，故后人稱該數列為斐波那契數列。接下來通過展示松果種子排列的螺線數目恰好是斐波那契數列中的數字，讓學生感受到簡單的數列背后蘊藏著大自然的規律，而這一現象直到1992年才有生物學上的解釋。斐波那契以他的兔子問題，猜中了大自然的奧秘。除此之外，該數列派生出了廣泛的應用，在19世紀末和20世紀成為熱門的研究課題，以至于1963年成立了斐波那契協會，還出版了《斐波那契季刊》。為了發現這些數字背后的奧秘，就需要求解其通項公式。

在這個教學過程中，教師以兔子繁殖問題為引例得到斐波那契數列，讓學生在體會數學之美的同時，激發學習興趣去探究該數列蘊藏的奧秘，為后面教學的展開做好鋪墊。

（三）? 斐波那契數列通項的求解

教師要滲透科學方法，引導同學們利用本課程所學的知識來考察n≥3時的遞推公式fn=fn-1+fn-2[9]。可以將fn看作是fn-1與fn-2這兩項的線性組合，而線性組合正是矩陣乘法的基本操作。因此可以構造如下2個向量：fnfn-1和fn-1fn-2，利用矩陣乘法得到如下遞推關系：fnfn-1=1? 11? 0fn-1fn-2，進而可得

若記M=1? 11? 0，則原問題轉化為求Mn-2。

這時引導學生思考，若存在可逆陣P和對角陣？撰，使得P-1MP=？撰，會得到什么結果呢？由P-1MP=？撰可得M=P？撰P-1，于是Mn-2=（P？撰P-1）n-2=P？撰n-2P-1，矩陣的冪轉化為容易計算的對角陣的冪，這正是數學運算和推理中常用的“化繁為簡”的思想，由此引出矩陣相似對角化的概念。

定義：設A與B為n階方陣，若存在n階可逆陣P，使得P-1AP=B，則稱A與B相似；若A與n階對角陣相似，則稱A可相似對角化。

這時引導學生進一步思考，是否任一n階方陣A都可相似對角化呢？若可以，可逆陣P和所相似的對角陣又該如何求得呢？由此引出矩陣相似對角化的性質和判別條件。

不妨設可逆陣P=（p1，p2，...，pn），對角陣？撰=diag（？姿1，？姿2，...，？姿n），則

因此，與A相似的對角陣對角線上的元素正是A的n個特征值，可逆陣P的各列正是分別屬于這n個特征值的特征向量。又因為P可逆，所以要求這n個特征向量必須線性無關。由此得到定理：n階方陣A可相似對角化當且僅當A有n個線性無關的特征向量。

基于以上分析，回到斐波那契數列通項的求解，要判斷M是否可相似對角化，首先由M的特征方程|？姿E-M|=？姿2-？姿-1=0，求得M有兩個不同的特征值？姿1=，？姿2=，進而求得屬于？姿1，？姿2的特征向量分別為p1=？姿11，p2=？姿21，由此可以判斷M一定可相似對角化，即令P=？姿1? ？姿21? ?1，有P-1MP=？撰=？姿1 0 0? ？姿2，故可求得

，

再由? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?可得斐

波那契數列的通項為

接下來，啟發同學們進一步思考，以上方法還能夠解決哪些更復雜的遞推關系求解問題呢？例如：

很顯然，這個遞推關系本質上仍然是線性組合，因此仍然可以使用矩陣法構造如下遞推關系

，

值得注意的是，其中方陣

的特征方程為？姿3-？姿2-？姿-1=0，計算得到一個實特征值和兩個復特征值，這里同學可能會質疑是否還可以應用矩陣的相似對角化來計算這個三階方陣的冪。這時需要強調上述推導的矩陣可相似對角化條件與特征值和特征向量是否為實的并無關系。通項的具體形式可以留給同學們課后進行探索。

在這個教學過程中，教師利用特殊數列的通項求解過程，著重培養學生的數學素養和科學思維，求解方法體現了“化繁為簡”的數學思想。通過對問題的提升，激發學生思考應用矩陣法解決問題的本質是什么，加深學生對矩陣運算的理解，提高應用抽象的概念分析解決問題的能力，使學生體會到“從特殊到一般”的認知過程，領悟科學發展的規律，愿意挖掘自然界隱藏的奧秘。

（四）? 斐波那契數列背后的秘密

同學們會發現一個有趣的現象，一個由自然數構成的數列，通項卻是用無理數表達的，使學生感受數學世界之神奇。接著引導學生探索該數列相鄰兩項比值的規律，前項與后項的比值：，，，，，，…，→==≈0.618，即比值的極限恰好是黃金分割比。這一分割比例在視覺上給人極大的愉悅感，因此成為工藝美術、建筑和攝影等許多藝術門類中審美要素，更是20世紀60年代，華羅庚先生創造的優選法的基礎。這里可以通過一個具體的例子簡單介紹優選法。煉鋼需要摻入某種化學元素加大鋼的強度，假設已知每噸鋼加入該化學元素的數量大約在1 000至2 000克，問摻入多少最佳？通常同學們會想到使用二分法來進行試驗，可以比較快速地逼近結果。但華羅庚先生證明了，每次取試驗區間的黃金分割處去做試驗才是最好的方法。接著通過華羅庚先生的人物事跡激發學生的愛國情懷。華羅庚先生是國際上享有盛譽的數學大師，被列為芝加哥科學技術博物館中當今世界88位數學偉人之一。其在新中國成立后的1950年，毅然決定放棄在美國的優厚待遇，攜夫人和孩子回到祖國。當時的中國積貧積弱，百廢待興，華羅庚先生在這樣的艱苦環境中不忘初心，在數學多個領域中碩果累累，培養出一批優秀數學家，開創了中國數學學派。面對我國一窮二白的境況，他在數學理論研究的同時，努力嘗試尋找一條數學和實踐相結合的道路，這使得優選法幫助工農業生產大大提高了效率[10]。

在這個教學過程中，通過斐波那契數列背后隱藏的黃金分割比，引出華羅庚先生心懷祖國、學以致用的報國情懷，同學們會想到現在的生活水平比起華羅庚年代有了質的飛躍，而這短短七十余年的發展凝聚了無數先輩的心血和付出，然而我國現在仍然有很多領域處于“卡脖子”的境地，使命感和責任感油然而生，更應該珍惜當下，努力學習，回饋國家和社會。

（五）? 拓展應用

通過以上學習，同學們知道了如何利用矩陣的相似對角化求矩陣的冪。事實上，很多實際問題都可以抽象為該類問題。以人口遷移問題為例，假設一個城市的總人口保持固定，初始時40%的人生活在城市，60%的人生活在郊區，然而每年有6%的人從城市搬到郊區，2%的人從郊區搬到城市，那么問若干年后城市和郊區的人口分布比例分別是多少呢[11]？

設xn和yn分別表示第n年城市人口占比和郊區人口占比，由題意可得xn=0.94xn-1+0.02yn-1yn=0.06xn-1+0.98yn-1，其中x1=0.4y1=0.6。這時引導同學觀察，得到其本質就是矩陣乘法運算：

，記為？琢n=A？琢n-1。通過遞推可以得到第n年的人口分布向量？琢n=An-1？琢1。這樣原問題就又轉化為矩陣求冪問題。由于矩陣A有兩個互異的特征值？姿1＝1，？姿2=0.92，特征向量分別為p1=13，p2=-1 1線性無關，因此一定可相似對角化，進一步求得

。原問題由此得以解決。

接下來教師進一步提出一個問題，很多很多年后，人口分布的比例又分別是多少呢，具有什么性質呢？引導學生思考矩陣方冪的極限

（1）

這時通過觀察，得到這個極限分布向量恰好是A的屬于特征值1的一個特征向量。

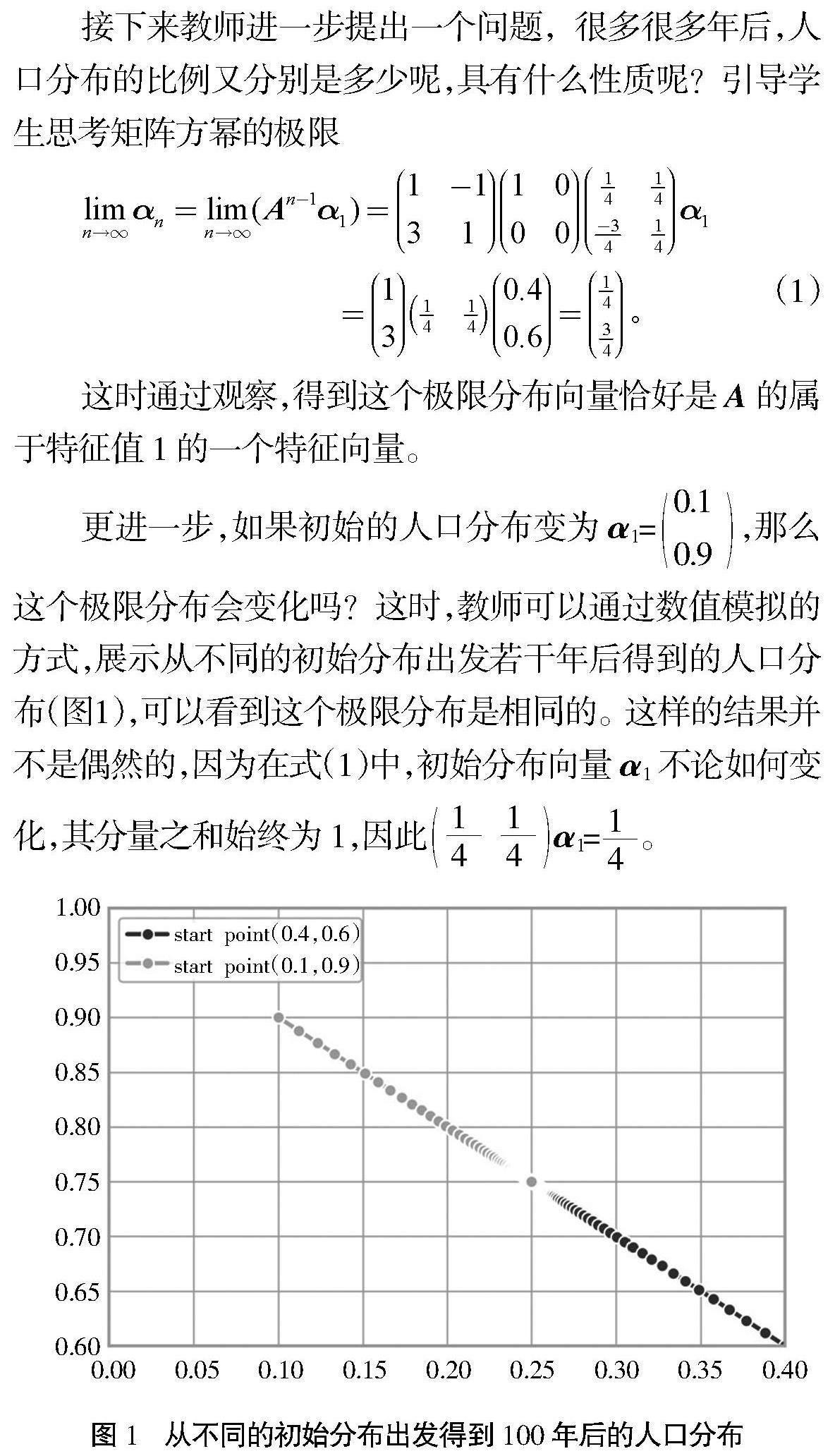
更進一步，如果初始的人口分布變為？琢1=0.10.9，那么這個極限分布會變化嗎？這時，教師可以通過數值模擬的方式，展示從不同的初始分布出發若干年后得到的人口分布（圖1），可以看到這個極限分布是相同的。這樣的結果并不是偶然的，因為在式（1）中，初始分布向量？琢1不論如何變化，其分量之和始終為1，因此 ？琢1=。

事實上，人口遷移的過程在統計學上稱為馬爾科夫鏈，即每個時刻的人口分布情況是由前一時刻的人口分布情況和矩陣A來確定的，這個矩陣稱為狀態轉移矩陣，所得的極限分布稱為馬爾科夫鏈的穩態。很多實際問題都可以用馬爾科夫鏈來建模，例如谷歌搜索引擎的PageRank算法、天氣預測、分子擴散模型等。那么是否馬爾可夫鏈都存在著穩態呢？這盡管不屬于本課程的內容，但鼓勵同學們在課后進行探索性研究：首先，應用所學知識動手證明若一個方陣任何一列的所有元素之和為1，則1一定是該方陣的特征值；其次，通過數值模擬的方式觀察狀態轉移矩陣對收斂性的影響，并猜想能夠產生長期穩定行為的狀態轉移矩陣所應滿足的性質；最后，查閱相關文獻資料驗證自己的猜想并撰寫研究報告。

在這個教學過程中，通過由淺入深、層層遞進的問題激發學生的求知欲望，讓學生體會“從特殊到一般，再從一般到特殊”的科學思維方法。通過案例的解決讓學生真正感到數學在實際問題的應用價值，增強從實際問題中概括提煉數學問題和概念的能力。用以促學，培養用所學知識解釋生活中現象的能力，增強勇于探索的科研精神。

三? 結束語

本案例設計從簡單的問題出發，層層遞進地引出背后的數學原理，符合大一新生的認知規律和實際水平，讓學生克服“數學難學”的固有認知。由圖片展示、數值模擬、人物故事等營造出輕松活躍的教學氛圍，通過探索斐波那契數列背后隱藏的奧秘使學生體會數學之美，通過解決實際中遇到的問題讓學生感受到數學有用，進而激發學生自主學習探索的興趣。通過案例教學，讓同學們掌握應用矩陣方法描述問題，以及應用矩陣相似對角化求矩陣方冪的具體過程和方法，學會“化繁為簡”的數學思想以及“從特殊到一般，再從一般到特殊”的科學思維方式。

通過課程內容延伸華羅庚先生的故事，以華羅庚先生“心懷祖國，學以致用”的高尚情懷感染學生，使學生感悟到作為新時代大學生的使命感和責任感，學習樹立正確的人生觀、世界觀、價值觀；同時通過思考解決實際中的應用案例，提高學生發現問題、分析問題、解決問題的能力，培養了學生獨立思考的能力和勇于探索的科研精神。

參考文獻：

[1] 高月鳳，劉錫平.線性代數課程思政教學方案設計與實踐[J].大學數學，2023，39（3）：20-24.

[2] 蘇克勤，曹殿立，姬利娜，等.線性代數課程思政的設計與教學實踐[J].高教學刊，2021，7（27）：189-192.

[3] 王淑霞，閻欣華，杜建衛.“線性代數”課程思政案例探索與實踐[J].教育教學論壇，2023（32）：98-101.

[4] 文軍，王宇，屈龍江.思政要素有機融入課程——以《線性代數》為例[J].高等數學研究，2023，26（4）：54-58.

[5] 楊威，陳懷琛，劉三陽，等．大學數學類課程思政探索與實踐——以西安電子科技大學線性代數教學為例[J].大學教育，2020，2（3）：77-79.

[6] 吳國麗.案例式教學法在線性代數課程中的應用[J].高教學刊，2018（20）：102-104.

[7] 馮杰，楊慧，董連春.基于案例教學的“線性代數”課程教學創新與研究——以矩陣的特征值特征向量為例[J].科技風，2023（12）：120-122.

[8] 顧沛.數學文化[M].2版.北京：高等教育出版社，2017.

[9] 李尚志.線性代數[M].北京：高等教育出版社，2011.

[10] 李健臣.為數學而生的大師：華羅庚[M].武漢：華中科技大學出版社，2020.

[11] 肖占魁，黃華林，林增強，等.應用線性代數[M].北京：機械工業出版社，2021.