數學文化類主題式教學的探索與實踐

徐友勇 周煉

[ 摘 要 ]文章從世界名畫《蒙娜麗莎》入手，以數學文化視角設計了藝術欣賞、工具開發、不同視角、綻放華彩、數字探秘、自然語言等活動，引導學生結合黃金分割等知識對該畫作進行深入的研究，并總結了關于數學文化類主題式教學的兩點建議.

[ 關鍵詞 ]數學文化；主題式教學；黃金分割；蒙娜麗莎；斐波那契數列

基金項目：2022年江蘇省教育科學規劃課題“大概念觀照下初中數學前建構教學的實踐研究”（C/2022/02/01）.

研究起源

2022年4月，教育部頒發《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”），并在“課程內容”中指出：“以培養學生綜合運用所學知識和方法解決實際問題的能力為目標，根據不同學段學生特點，以跨學科主題學習為主，適當采用主題式學習和項目式學習的方式.”另外，新課標在“課程性質”與“課程理念”中分別提到，“數學承載著思想和文化，是人類文明的重要組成部分”“關注數學學科發展前沿與數學文化”[1].主題式教學是響應新課標理念的先鋒性嘗試，沒有統一的教材，要求教師根據課程目標靈活設計教學過程，合理開發課程資源，具有較大的探索空間.近年，關于數學文化教育的研究雖層出不窮，但落實到具體課堂時依舊無法擺脫工具主義和科學主義帶來的單向性，無法真正將數學作為一種文化與生命存在的意義教給學生，而主題式教學提供了一種使文化擺脫知識束縛的突破口[2].本文以“從世界名畫到黃金螺線”為例，對數學文化融入主題式教學進行了探索與實踐，具有一定的實驗性與前瞻意義，以期為新課標的落實提供切實可行的創新型案例.

教學設計

1.藝術欣賞：從世界名畫說起

材料閱讀 如圖1，《蒙娜麗莎》（Mona Lisa）是意大利文藝復興時期畫家列奧納多·達·芬奇創作的油畫，現收藏于法國盧浮宮博物館.該畫作主要表現了女性典雅和恬靜的典型形象，塑造了資本主義上升時期一位城市有產階級的婦女形象.《蒙娜麗莎》代表了文藝復興時期的美學方向.該作品折射出來的女性深邃與高尚的思想品質，反映了文藝復興時期人們對于女性美的審美理念和審美追求.

問題1 你認為《蒙娜麗莎》這幅畫美在哪里？可以從不同角度談談你的想法.

活動1 眼睛是心靈的窗戶，如果將《蒙娜麗莎》中兩只眼睛的端點分別視為一條直線上的四個點A，B，C，D，并測量其中的線段的長，你發現了什么？

學生展示 學生在繪圖紙上描點、畫線、測量，并在計算后得到了接近黃金比的數值.

畫板驗證 教師運用幾何畫板構造點B是AC，AD的黃金分割點，點C是BD，AD的黃金分割點（如圖2），將其放縮并與眼睛比對后發現，兩者基本吻合.

問題2 你能結合圖2復習“黃金分割”的相關知識嗎？

設計意圖 《蒙娜麗莎》在藝術領域的舉足輕重地位，不僅體現在它獨特的歷史意義與人文價值上，其背后的美學原理更是不可多得的跨學科研究素材.該作品屬于人物肖像畫，俗話說“眼睛是心靈的窗戶”，讓學生從審美的發散性視角聚焦該畫作中足夠傳神的眼睛是較為合適的.將眼睛抽象為點與線段后，學生通過畫圖、測量、計算等一系列活動，既能順利回憶起“黃金分割”的相關知識，又豐富了藝術鑒賞方式，將數學與美學巧妙地融合，這正是數學作為一種文化的高度體現.

2.工具開發：再研究世界名畫

問題3 《蒙娜麗莎》極高的審美價值一定不只與眼睛有關，同學們認為該畫作中還有哪些地方也能體現出黃金分割？僅靠一把刻度尺夠嗎？

學生質疑 在活動1中，以畫作中的眼睛為目標的畫圖、測量、計算已占用不少時間，若換成無目的地操作，將不利于大家對全畫進行高效、深入的研究.

學具說明 看來刻度尺已無法勝任此項工作，我們有必要開發一種能直接看出黃金分割點的測量工具.教師查閱資料后發現“黃金分割尺”具備這樣的功能.黃金分割尺：用螺釘將兩根長度相等的木條AB，AC的端點A固定，點D是木條AB的黃金分割點，并在木條AC上取點F，使得CF=BD.再取一根與BD長度相同的木條DE，將其固定在D點處，并在木條DE上取點G，使得DG=AD.最后取一根與AD長度相同的木條FG，并將其兩端分別固定在點F，G處（如圖3），那么點E為線段BC的黃金分割點[3].

問題4 若將“黃金分割尺”抽象成幾何圖形（如圖4），你能對其運作原理進行證明嗎？

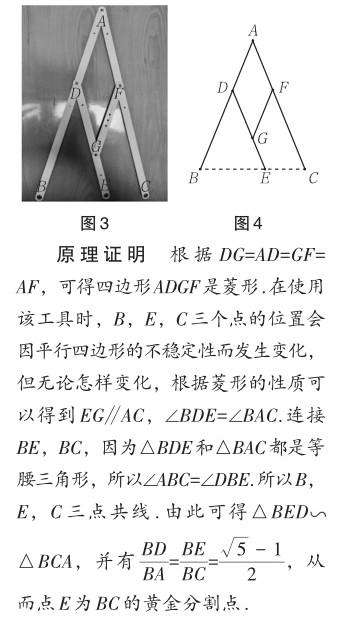
設計意圖 學生初學黃金分割時，教師曾用“芭蕾舞演員”“東方明珠”等情境引入，但這些素材均是從高度體現黃金分割的.《蒙娜麗莎》中有多處蘊藏了黃金比，假如依舊通過測量、計算的方式研究明顯是不高效的，因此產生了引入“黃金分割尺”的必要性.接著，教師讓學生分析“黃金分割尺”的構造，證明其操作原理.證明“黃金分割尺”的操作原理時，學生綜合運用了相似三角形、菱形、等腰三角形等知識，對黃金分割進行了知識的再建構.事實上，將黃金分割作為開發一種新工具的制作原理，這本身也是數學投身于生產、制造方面的一種文化價值體現.

3.不同視角：別樣的黃金分割

活動2 利用“黃金分割尺”找到畫作中其他符合黃金比的部位，并將黃金分割點標注出來，利用平板拍照上傳至班級云空間，及時共享研究成果.

問題5 從同學們上傳的照片來看，你們找到了很多除眼睛外能體現黃金比的部位，如鼻子、下巴等.事實上，這些部位均能抽象為某條線段.若研究視角由線上升到面，你們認為蒙娜麗莎的臉也符合黃金比嗎？

設計意圖 在前兩個環節中，學生對黃金分割的認識依舊停留在點、線層面，哪怕是引入“黃金分割尺”后也僅僅增加了研究的開放性.當教師啟發學生將視角從眼睛蔓延到臉部、從線上升到面時，便順勢由黃金分割點引出黃金矩形.黃金矩形的出現不僅承接了前面黃金分割知識的運用，也是后續研究五角星、斐波那契數列、黃金螺線等體現數學文化內容的知識起點，其在整節課中起到了承上啟下的關鍵作用.

4.綻放華彩：黃金矩形的演變

活動3 你能借助“黃金分割尺”在透明紙上作一個寬為5 cm的黃金矩形嗎？在作出黃金矩形的基礎上，你能通過尺規再作出一個黃金三角形嗎？請5人為一組，討論用這些全等的黃金三角形能否拼出五角星，并給出具體方案.

學生展示 分別以點C，D為圓心，以矩形長為半徑畫弧交于點E，得到黃金三角形CDE（如圖6），并以底邊首尾相接的形式將5個黃金三角形拼成五角星.

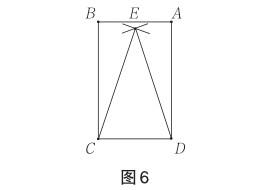
畫板驗證 由于正五邊形的中心角是72°，通過幾何畫板將黃金三角形繞著中心依次迭代旋轉4次（如圖7），便可得到一個五角星（如圖8）.此時，再運用“動畫”的“顯示”功能，將五角星呈現于“五星紅旗”之上（如圖9）.

設計意圖 設計在黃金矩形的基礎上作黃金三角形這一活動，不僅可以讓學生體驗以黃金比設計圖形的美學文化，也發展了學生的作圖能力與推理素養.另外，五角星是以黃金比構造圖形的極致體現，最早被發現在公元前3000年的美索不達米亞文獻中，其本身就蘊含了豐富的數學文化.在本節課中，無論是讓學生拼五角星，還是在畫板中演示五角星的生成過程，均讓學生參與了數學文化的創造過程.最后，將五角星在國旗上呈現更是將數學文化與愛國主義教育相結合，在國內外文化的碰撞與融合中為學科育人提供了一種新的視角.

5.數字探秘：黃金矩形的真相

材料閱讀 除了能演變為五角星的黃金矩形，在數學史上有一類矩形也很出名，它們由斐波那契數列構造而成.斐波那契數列的前兩項均為1，后面每一項均由前兩項相加得來，如：1，1，2，3，5，8，13，21…從邊長為1，1開始，依次往后取兩項作為寬與長，可以構造一類矩形.

問題6 你認為黃金矩形與這類矩形有什么關系？

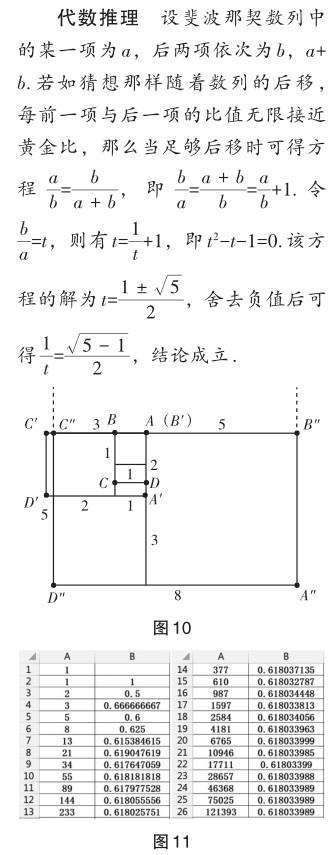
畫板驗證 利用幾何畫板的“放縮”功能，將黃金矩形拖動至由斐波那契數列構成的矩形處進行比對（如圖10）.發現隨著斐波那契數列的后移，這類矩形越來越接近黃金矩形.

問題7 你能否從數的角度，進一步驗證你的猜想？

計算驗證 打開Excel軟件，在A1欄輸入1，A2欄輸入1，A3欄輸入A1+A2，往下拖動即可形成斐波那契數列.接著在B2欄輸入A1/A2，往下拖動即可形成斐波那契數列前一項與后一項的比值.發現該比值隨著數列的后移，確實越來越接近于黃金比（如圖11）.

問題8 無論是比對圖形還是計算比值，都僅僅是通過研究有限種情況進行的猜想.你能對該結論的一般性進行證明嗎？

設計意圖 黃金矩形與斐波那契數列之間有密切的關系，但又有“形”與“數”的本質區別，如何由“形”到“數”自然過渡是需要教師重點思考的問題.設計以黃金矩形比對用斐波那契數列構造矩形的實驗，是為了引導學生從圖形角度初步感悟兩者之間的關聯，接著借助Excel軟件從“數”的角度計算驗證，最后通過代數推理完成證明.這一探索過程中的數形結合、合情猜想、推理論證等元素均是數學文化中思想與方法的體現，能讓學生以數學文化視角來研究數學文化，進而揭示黃金矩形背后的數學真相.

6.自然語言：優美的“黃金螺線”

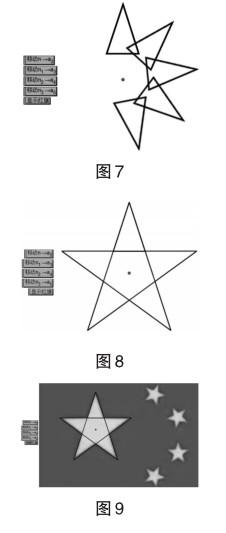
材料閱讀 在黃金矩形中靠著三邊作正方形，剩下的部分也是黃金矩形，可以依次再作正方形.將這些正方形的頂點按順序連接，可以得到一條“黃金螺線”.在由斐波那契數列構成的矩形中，從最小的矩形開始依次畫弧，構成的曲線可以近似地視為“黃金螺線”（如圖12）.

文化欣賞 之前同學們發現《蒙娜麗莎》中有多處符合黃金比，事實上整幅畫就處于“黃金螺線”之中（如圖13）.“黃金螺線”廣泛存在于自然界、藝術、建筑等領域，如帕特農神廟（如圖14）、銀河系（如圖15）.由此可見，數學作為大自然的語言，既是我們生活的世界的重要組成部分，也促進了人類文明的發展.