數(shù)學(xué)概念生成性教學(xué)研究

摘要：概念教學(xué)是數(shù)學(xué)教學(xué)的重點(diǎn)和難點(diǎn)。重視數(shù)學(xué)概念生成性的教學(xué)有助于學(xué)生理解概念的本源和內(nèi)涵。本文提出了數(shù)學(xué)概念生成性教學(xué)的三個策略：“問題鏈”式教學(xué)策略、追溯數(shù)學(xué)概念的本源性策略、教師主導(dǎo)學(xué)生主體互動策略。并以初中“函數(shù)”概念的教學(xué)為例，從概念引入環(huán)節(jié)、概念形成環(huán)節(jié)、概念剖析環(huán)節(jié)和概念擴(kuò)展延伸環(huán)節(jié)闡述三個策略的應(yīng)用，為數(shù)學(xué)概念生成性教學(xué)提供參考。

關(guān)鍵詞：數(shù)學(xué)概念" 生成性教學(xué)" 初中數(shù)學(xué)" 函數(shù)

隨著新課程改革的不斷推進(jìn)，培養(yǎng)學(xué)生的核心素養(yǎng)成為教育的一個重要目標(biāo)。概念教學(xué)是數(shù)學(xué)教學(xué)的重點(diǎn)，也是難點(diǎn)，在學(xué)生數(shù)學(xué)素養(yǎng)培養(yǎng)方面具有重要意義。函數(shù)概念是初中數(shù)學(xué)基本的、重要的概念，同時也是高中數(shù)學(xué)的基礎(chǔ)。函數(shù)概念具有高度的抽象性，教學(xué)過程中，如果只以教師為教學(xué)的主體，而學(xué)生的學(xué)習(xí)方式主要是題海戰(zhàn)術(shù)，那么教學(xué)枯燥無趣，學(xué)生只能以被動的方式進(jìn)行學(xué)習(xí)，不僅學(xué)到的知識有限，而且能力的提升也較為緩慢，制約了學(xué)生素養(yǎng)的發(fā)展。因此，教學(xué)中需要改變學(xué)生學(xué)習(xí)方法和教師教學(xué)方法，讓每一位學(xué)生主動參與學(xué)習(xí)的過程，體驗(yàn)函數(shù)概念的產(chǎn)生過程，理論與實(shí)踐有機(jī)結(jié)合，這樣有助于學(xué)生更加深入地理解函數(shù)概念的本質(zhì)。本文以初中“函數(shù)”概念的教學(xué)為例，探討數(shù)學(xué)概念生成性教學(xué)。

一、概念生成性教學(xué)的內(nèi)涵

學(xué)術(shù)界從不同角度對概念生成性教學(xué)的內(nèi)涵進(jìn)行了界定。從生成性教學(xué)的過程來看，教師通過向?qū)W生提供新的知識信息，可以給他們帶來一定的刺激，促使學(xué)生將新的知識信息與原有的認(rèn)知結(jié)構(gòu)進(jìn)行聯(lián)系，在這個過程中，學(xué)生形成了關(guān)于新的知識信息的意義。從生成性教學(xué)的形態(tài)來看，它是一種在合適時機(jī)摒棄傳統(tǒng)教學(xué)規(guī)則并進(jìn)行靈活調(diào)整的教學(xué)形式。教師可以根據(jù)上課時師生互動情況，了解學(xué)生的學(xué)習(xí)行為并引導(dǎo)學(xué)生更好地消化和吸收課堂知識，讓課堂教學(xué)始終充滿活力。從生成性教學(xué)的角度來看，由于生成能力屬于人類認(rèn)知結(jié)構(gòu)的基本功能，因此任何學(xué)生都有可能產(chǎn)生生成效果，這些效果體現(xiàn)為為學(xué)生提供發(fā)展機(jī)會，以及生成新的知識和意義。

綜上所述，生成性教學(xué)是指，教師根據(jù)教學(xué)情況，在彈性預(yù)設(shè)的前提下，靈活且合理地設(shè)計(jì)教學(xué)活動，并在不斷變化的動態(tài)教學(xué)形態(tài)中，推動學(xué)習(xí)者不斷發(fā)展。

二、初中數(shù)學(xué)概念生成性教學(xué)的策略

（一）“問題鏈”式教學(xué)策略

在數(shù)學(xué)知識體系中，學(xué)生對概念性知識的掌握程度是后續(xù)學(xué)習(xí)的基礎(chǔ)，有些概念貼近生活，很容易理解，有些概念離生活較遠(yuǎn)，難以理解，相對來說不易掌握，教師應(yīng)采用生成性的教學(xué)方法，為抽象的數(shù)學(xué)概念提供生成條件，使學(xué)生以更能接受的方式理解和掌握所學(xué)的數(shù)學(xué)概念。“問題鏈”式教學(xué)法能夠?yàn)榇颂峁椭皢栴}鏈”式教學(xué)法指在教學(xué)過程中，教師按照教學(xué)目標(biāo)將教學(xué)內(nèi)容設(shè)置成以問題為紐帶、以形成和發(fā)展學(xué)生思維能力為主線、以師生合作互動為基本形式的教學(xué)模式。

1.“問題鏈”式教學(xué)在數(shù)學(xué)概念生成中的作用

“問題鏈”式教學(xué)可以引導(dǎo)學(xué)生的思維層層遞進(jìn)，幫助學(xué)生從生活經(jīng)驗(yàn)中抽象出數(shù)學(xué)概念，具體有多方面的作用。

第一，通過教師與學(xué)生的互動，生成性教學(xué)模式能夠提升學(xué)生的參與度，從而增強(qiáng)學(xué)生的自覺性和主動性。與傳統(tǒng)單向灌輸?shù)慕虒W(xué)模式不同，生成性教學(xué)模式通過引導(dǎo)學(xué)生從抽象走向具體、從概念走向事實(shí)，讓學(xué)生成為課堂的主體，深刻感受數(shù)學(xué)概念的形成過程。

第二，生成性教學(xué)模式能夠增強(qiáng)教學(xué)的針對性。由于不同學(xué)生的基礎(chǔ)知識和思維方式存在差異，設(shè)計(jì)問題鏈可以根據(jù)不同層次、不同思維水平的學(xué)生進(jìn)行針對性的調(diào)整。這樣能夠讓數(shù)學(xué)概念更貼近生活，貼近學(xué)生的原有認(rèn)知水平，幫助學(xué)生更好地理解和生成數(shù)學(xué)概念。

第三，保證教學(xué)連貫性。設(shè)計(jì)問題鏈不是簡單地將問題進(jìn)行組合，問題是具有連續(xù)性的，能夠起到承上啟下的作用。初中階段數(shù)學(xué)概念基本是從某個情境中生成的，情境作用的發(fā)揮離不開問題鏈的環(huán)環(huán)相扣，而且部分?jǐn)?shù)學(xué)概念之間存在一定的聯(lián)系。通過對數(shù)學(xué)概念進(jìn)行細(xì)化、分解而形成問題體系，能夠保證教學(xué)的連貫有序、層層遞進(jìn)，確保了數(shù)學(xué)概念生成過程中，形成嚴(yán)密的邏輯閉環(huán)。

2.“問題鏈”式教學(xué)數(shù)學(xué)概念生成的設(shè)計(jì)策略

“問題鏈”式教學(xué)要注重問題之間形成邏輯鏈條，通過設(shè)置學(xué)生感興趣的問題激發(fā)學(xué)生的內(nèi)驅(qū)力，并讓問題環(huán)環(huán)相扣。教師圍繞問題，引導(dǎo)學(xué)生積極探索數(shù)學(xué)概念的形成過程，營造良好的互動氛圍，接下來筆者淺談“問題鏈”式教學(xué)模式下數(shù)學(xué)概念生成的基本策略。

第一，“問題鏈”式教學(xué)可以提升學(xué)生對數(shù)學(xué)概念的感知能力。學(xué)生對數(shù)學(xué)概念的準(zhǔn)確性、清晰性和完整性的把握，對于他們掌握基礎(chǔ)知識、法則和公式等各種數(shù)學(xué)技能至關(guān)重要。“問題鏈”式教學(xué)通過設(shè)計(jì)一系列有機(jī)銜接的問題，引導(dǎo)學(xué)生從抽象走向具體、從概念走向事實(shí)，使學(xué)生深入感受數(shù)學(xué)概念的形成過程，從而提高他們對數(shù)學(xué)概念的感知能力。

第二，采用加強(qiáng)學(xué)生比較思維的策略，有助于提高數(shù)學(xué)概念形成過程中的理解能力。利用比較思維進(jìn)行知識遷移，是常用的教學(xué)方法之一，在利用比較思維生成數(shù)學(xué)概念的過程中，也可以利用“問題鏈”式教學(xué)法實(shí)現(xiàn)教學(xué)目標(biāo)。

（二）追溯數(shù)學(xué)概念的本源性策略

1.追溯數(shù)學(xué)概念本源性策略的作用

本源性問題往往隱藏在知識的背后，它具有一定的隱蔽性，所以數(shù)學(xué)概念的學(xué)習(xí)應(yīng)圍繞本源性問題展開，充分挖掘概念產(chǎn)生的背景，讓學(xué)生理解學(xué)習(xí)數(shù)學(xué)概念的必要性和重要性，激發(fā)學(xué)生的好奇心和學(xué)習(xí)興趣。數(shù)學(xué)學(xué)科中存在許多有著豐富歷史背景與起源的概念，教師在具體的教學(xué)過程中，如果能夠?qū)⑦@些歷史背景與起源、數(shù)學(xué)故事進(jìn)行巧妙的設(shè)計(jì)，必然激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)概念的興趣，學(xué)生通過追根溯源和探知前人的認(rèn)知過程，自然也會對數(shù)學(xué)概念的本質(zhì)產(chǎn)生更加深入的理解。

2.追溯數(shù)學(xué)概念本源性的設(shè)計(jì)策略

數(shù)學(xué)概念的生成離不開充分挖掘概念的產(chǎn)生背景，這就要求教師一方面在課堂上透過數(shù)學(xué)概念的表象，把握知識的本質(zhì)，進(jìn)而構(gòu)建知識體系，使學(xué)生更好地掌握知識的本質(zhì)，讓學(xué)生明白概念產(chǎn)生的緣由；另一方面教師設(shè)身處地地從學(xué)生的角度思考問題。處于初中階段的學(xué)生尚不具備充足的知識儲備和一定的理解能力，教師要有前瞻性地將學(xué)生不理解的問題設(shè)計(jì)為本源性問題，引發(fā)學(xué)生思考。

（三）教師主導(dǎo)學(xué)生主體互動策略

1.教師主導(dǎo)學(xué)生主體互動策略的作用

在數(shù)學(xué)概念生成性教學(xué)中，為體現(xiàn)學(xué)生的主體地位，需要突出教學(xué)活動是在教師的引導(dǎo)下，學(xué)生充分參與課堂并自主探究，對教授的內(nèi)容進(jìn)行理解和感受，從而在學(xué)習(xí)中獲得新的體驗(yàn)，達(dá)到數(shù)學(xué)概念的自主生成。

2.教師主導(dǎo)學(xué)生主體互動策略的設(shè)計(jì)

教師主導(dǎo)學(xué)生主體的互動策略需要教師創(chuàng)設(shè)問題情境，激發(fā)學(xué)生的創(chuàng)新思維，營造活躍的課堂氛圍，適時開展合作交流，對學(xué)生的學(xué)習(xí)過程作出合理引導(dǎo)，從而取得教師主導(dǎo)學(xué)生主體的教學(xué)效果。

三、初中數(shù)學(xué)“函數(shù)”概念生成性教學(xué)設(shè)計(jì)

（一）概念引入環(huán)節(jié)

關(guān)于函數(shù)概念的引入，可以通過以下幾個問題幫助學(xué)生進(jìn)入課堂學(xué)習(xí)狀態(tài)，引出本節(jié)課的重點(diǎn)。

問題一：老師去超市買蘋果，發(fā)現(xiàn)蘋果的單價是12元每千克，那么蘋果凈重和蘋果總價有什么關(guān)系呢？

問題二：在期末考試中，成績排行榜中有兩個量：學(xué)號和成績，那么一個學(xué)號能否有確定的成績和它相對應(yīng)？如果有，是一個還是多個？

問題三：同學(xué)們有看過《名偵探柯南》嗎？其中有一個場景是警察根據(jù)案發(fā)現(xiàn)場的腳印長度和寬度，推斷出犯罪嫌疑人的身高，這是什么原理呢？

通過這三個日常生活中大部分學(xué)生都見過，但并未對其中的道理進(jìn)行深入思考的問題，引入本節(jié)課所講解的函數(shù)概念。雖然這個時候?qū)W生并不能真正生成函數(shù)概念，但能在這三個問題中感受到我們?nèi)粘Ｉ钪泻芏嗍虑槭谴嬖谝欢ㄒ?guī)律的，如問題二中學(xué)號和成績是一一對應(yīng)的關(guān)系，一個學(xué)號對應(yīng)著唯一的成績，從而激發(fā)學(xué)生學(xué)習(xí)的主動性，并為后續(xù)概念生成打下良好的基礎(chǔ)。

（二）概念生成環(huán)節(jié)

概念生成是教師提供豐富案例，讓學(xué)生進(jìn)行自主探究的過程。函數(shù)概念的生成，是基于學(xué)生對常量和變量概念的理解，此處主要采用教師主導(dǎo)學(xué)生主體的策略，使學(xué)生通過對實(shí)際問題的操作，體會數(shù)學(xué)在生活中的應(yīng)用，幫助學(xué)生生成數(shù)學(xué)概念。

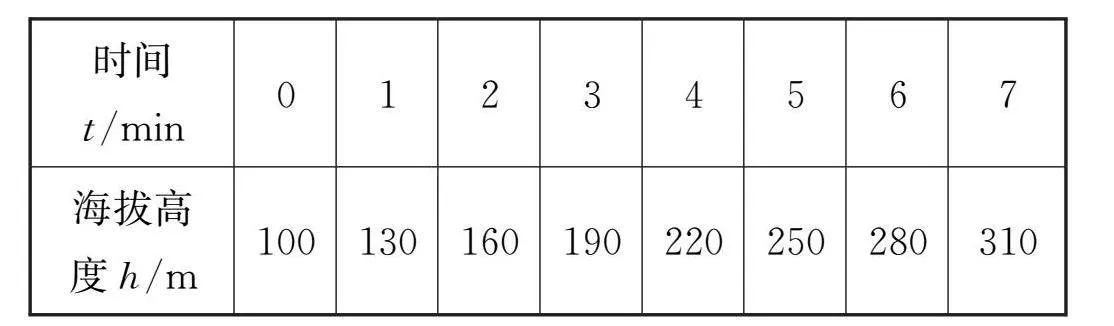
活動：播放熱氣球升空視頻，并假設(shè)熱氣球從海拔100 m處的某地升空，在它逐漸上升的過程中，海拔高度h（m）與上升時間t（min）的關(guān)系記錄如下：

（1）這次活動涉及哪幾個量？

（2）觀察表格中的數(shù)據(jù)，熱氣球升空的過程中速度為多少？

（3）哪些量發(fā)生變化？哪些量沒發(fā)生變化？

（4）熱氣球高度隨時間推移有什么變化規(guī)律嗎？

（5）你能總結(jié)出h和t的關(guān)系嗎？

（6）在上升時間為9 min和22 min時，熱氣球所處位置的海拔高度為多少米？

教師活動：組織學(xué)生集體交流，并尋找合適契機(jī)對表格中的數(shù)據(jù)進(jìn)行分析。

該活動的（1）、（2）、（3）問通過學(xué)生對表格信息的討論，容易得出熱氣球原來所在的高度、熱氣球上升的速度是不變的，熱氣球升空的時間和熱氣球海拔高度是發(fā)生變化的，這時教師可以引導(dǎo)學(xué)生總結(jié)常量和變量的定義，并掌握判斷一個量是常量還是變量的方法。而（4）、（5）、（6）問幫助學(xué)生生成自變量和因變量的概念，從而得出函數(shù)的定義。

通過六個問題組成的“問題鏈”，讓學(xué)生在自主探究與合作交流活動中，充分經(jīng)歷新知識的發(fā)生與發(fā)展過程，使學(xué)生有效地理解并掌握常量與變量、自變量與因變量及函數(shù)的定義。

（三）概念剖析環(huán)節(jié)

通過對教材的研讀不難發(fā)現(xiàn)，函數(shù)單元的教學(xué)設(shè)計(jì)中情景教學(xué)居多，大部分是由實(shí)際問題抽象出相對應(yīng)的函數(shù)問題，由此研究函數(shù)的概念，這有利于培養(yǎng)學(xué)生綜合應(yīng)用數(shù)學(xué)知識的能力和實(shí)踐意識。然而在學(xué)習(xí)函數(shù)概念的過程中，教師或?qū)W生將側(cè)重點(diǎn)經(jīng)常放在后續(xù)研究函數(shù)的應(yīng)用上，因此容易忽略函數(shù)自身內(nèi)涵和外延的剖析。根據(jù)初中函數(shù)概念的定義：一般地，在一個變化過程中，如果有兩個變量x和y，并且對于x的每一個確定的值，y都有唯一確定的值與其對應(yīng)，我們就把x稱為自變量，把y稱為因變量，y是x的函數(shù)。教師可以引導(dǎo)學(xué)生剖析以下兩個問題，幫助學(xué)生了解函數(shù)概念的內(nèi)涵和外延。

問題一：在函數(shù)的概念中有“在某個變化過程中，有兩個變量x、y”這一前提條件，請同學(xué)們根據(jù)這個條件，判斷圓的面積公式S=πr2中，π和r是否可以構(gòu)成函數(shù)關(guān)系。

問題二：為什么函數(shù)的定義是“在某個變化的過程中”？

以上兩個問題，問題一幫助學(xué)生理解函數(shù)概念的外延，概念的外延是指具有概念所反映的特有屬性的事物，通過讓學(xué)生判斷圓的面積公式中π和r是否可以構(gòu)成函數(shù)關(guān)系，來考查學(xué)生對函數(shù)概念的外延是否充分掌握。問題二幫助學(xué)生理解函數(shù)概念的內(nèi)涵，概念的內(nèi)涵是指概念所反映的事物的特有屬性，是概念必須具有的內(nèi)容，那么可以通過一個具體的例子來解釋問題二。在物理公式s=vt中，當(dāng)時間是固定的一個值，那么速度與路程就構(gòu)成了一個函數(shù)，速度越大則路程越長，在這個函數(shù)中，速度是自變量，路程是因變量，時間是常量；當(dāng)速度是固定的一個值，那么時間和路程構(gòu)成了一個函數(shù)，時間越長則路程越長，在這個函數(shù)中，時間是自變量，路程是因變量，速度是常量。綜上所述，變量和常量都是相對于一個變化的過程而言的，沒有絕對的變量和常量。

（四）課后拓展延伸環(huán)節(jié)（追溯概念本源）

學(xué)完函數(shù)概念，在教師布置的課后作業(yè)中，可以讓學(xué)生查閱資料，了解人類為什么要創(chuàng)造函數(shù)。學(xué)生可以發(fā)現(xiàn)在16世紀(jì)和17世紀(jì)，歐洲資本主義國家為占領(lǐng)更多資源，不斷發(fā)起戰(zhàn)爭，大力發(fā)展航運(yùn)、武器等工業(yè)體系。而發(fā)展航運(yùn)工業(yè)體系，就需要確定船只在海洋中的位置以及地球上的經(jīng)緯度。同時在戰(zhàn)爭中想要取得勝利，也需知道如何向正確位置發(fā)射炮彈等一系列問題，這就促使人們需要對不同“運(yùn)動”中的數(shù)量關(guān)系進(jìn)行深入研究，這種歷史背景為函數(shù)概念的產(chǎn)生提供了客觀條件。

了解這些背景能夠讓學(xué)生更清楚地認(rèn)識到數(shù)學(xué)概念不是憑空產(chǎn)生的，而是通過發(fā)現(xiàn)問題并經(jīng)過仔細(xì)研究而提出的，具有重要的意義。其實(shí)在解決生活中的困難時，難免遇到問題，而遇到問題則是數(shù)學(xué)家們展開研究的動機(jī)，這樣的問題同樣也可以成為學(xué)生研究和學(xué)習(xí)的動機(jī)。

與此同時，教師也可以布置一項(xiàng)讓學(xué)生觀察日常生活中的函數(shù)關(guān)系的作業(yè)，如家里的水費(fèi)和電費(fèi)是按照什么樣的規(guī)則計(jì)算的，是否可以寫成函數(shù)關(guān)系？坐出租車時，司機(jī)是按照什么樣的規(guī)則計(jì)價收費(fèi)的，是否也可以寫成函數(shù)關(guān)系？下次上課時，教師可以組織學(xué)生對生活中的函數(shù)關(guān)系進(jìn)行交流討論，說明自己得出函數(shù)關(guān)系的過程，應(yīng)用了哪些知識，讓數(shù)學(xué)概念回歸于生活，同時培養(yǎng)學(xué)生舉一反三的能力。

結(jié)語

生成性教學(xué)已逐漸成為現(xiàn)代教育研究的一個熱門話題。數(shù)學(xué)概念作為數(shù)學(xué)的細(xì)胞，如何進(jìn)行數(shù)學(xué)概念的生成性教學(xué)，如何更好地捕捉課堂上的生成性資源，如何促進(jìn)數(shù)學(xué)概念的有效生成，已成為一線數(shù)學(xué)教師關(guān)注的焦點(diǎn)。因此，生成性教學(xué)無論是在數(shù)學(xué)概念的教學(xué)中，抑或是在其他方面的教學(xué)中，都值得推廣和應(yīng)用，促進(jìn)學(xué)生有效學(xué)習(xí)，提高教學(xué)質(zhì)量。

參考文獻(xiàn)：

[1]余國良.生成性教學(xué)：概念、特征與路向[J].教育實(shí)踐與研究，2019（4）：49.

[2]呂榮平.高一物理概念生成性教學(xué)設(shè)計(jì)策略研究[D].蘭州：西北師范大學(xué)，2017.

[3]顧曉莉.利用數(shù)學(xué)史開展生成性教學(xué)——以復(fù)數(shù)概念的教學(xué)為例[J].中學(xué)數(shù)學(xué)，2019（15）：2425.

[4]任建文.高中數(shù)學(xué)概念生成過程“問題鏈”式教學(xué)設(shè)計(jì)研究[J].數(shù)學(xué)教學(xué)通訊，2017（21）：1516.

責(zé)任編輯：唐丹丹