談教學情境創設的幾個策略

陳永忠

〔關鍵詞〕 數學教學；教學情境；創設；策略

〔中圖分類號〕 G633.6

〔文獻標識碼〕 A

〔文章編號〕 1004—0463（2013）08—0076—01

新課標強調，讓學生在現實情境和已有的生活、知識經驗的基礎上學習和理解數學。這就要求教師要根據教學內容和學生的實際創設問題情境，指導學生通過問題的探究，實現知識上的突破。下面，筆者結合教學實踐，就教學情境的創設談幾點體會。

1.引疑激趣策略。烏申斯基指出：“沒有絲毫興趣的強制性學習，將會扼殺學生探求真理的欲望”。因此，教師設計的問題，要新穎別致，使學生有趣味感和新鮮感。

案例1：“二分法”的引入

央視著名節目主持人李詠主持的“非常6+1”中有一個欄目叫“競猜價格”，你知道如何才能最快猜準某個事物的價格嗎？“一石激起千層浪”，學生紛紛議論。趁機我又設計了一個小游戲：同桌相互猜生日，看誰能用“最少的次數”猜出對方的生日？

2.設置坡度策略。心理學家把問題從提出到解決的過程稱為“解答距”，并根據“解答距”的長短把它分為“微解答距”、“短解答距”、“長解答距”和“新解答距”四個級別。教師設計問題應考慮以上四個“解答距”級別，也就是要設計出有坡度的問題。讓學生通過做由易到難、由簡到繁的習題，最終達到掌握知識、培養能力的目的。

案例2：

問題1 1+2+3+…+100=？這是學生小學就已具備的高斯求和知識，學生可以解決。

問題2 能否用上述方法解決等差數列的前幾項和Sn？從特殊到一般Sn=（a1+an）+（a2+an-1）+……

問題3 （a1+an）=（a2+an-1）=……是否成立？

問題4 按例3中的分法把n項兩項兩項分為一組，可分多少組？學生經過討論，得出結論：取決于n的奇、偶性。

3.巧設懸念策略。懸念能給學生一種強烈的刺激，使學生產生“欲罷不能”的期待，進而激發學生的求知欲，調動起學生學習的熱情。

案例3：今天以后的22012天是星期幾？這樣的問題喚起了學生對二項式定理應用的濃厚興趣。在學生的認識沖突處導入新課，使學生產生“欲知而后快”心理，能激發起學生不斷探求的欲望。

4.以形助數策略。華羅庚說過：“數缺形時少直觀，形少數時難入微”。數形結合是研究數學的重要方法，“以形助數”是數形結合的主要方面，它借助圖形的性質，可以加深對概念、公式、定理的理解，體會概念、公式、定理的幾何意義。

案例4：已知函數f（x）是定義在R上的奇函數，當x≥0時，f（x）=x（1+x）。畫出函數f（x）的圖象，并求出函數f（x）的解析式。

學生在完成此題的過程中，通過作圖，找到特殊點，然后再確定x<0時f（x）的解析式。在完成此題目的基礎上，引導學生盡一步發問：此方法可以推廣嗎？對一般的奇函數也適用嗎？ 若f（x）為偶函數又該怎么處理？經過這樣一連串的發問，那么該題目的解決過程就顯得豐滿、充實。

5.聯系實際策略。新課標強調，從學生已有的生活經驗出發，讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程。在數學教學中，教師應根據生活和生產的實際創設問題情境，使學生認識到數學學習的現實主義，這樣也更容易激發學生的好奇心和興趣。

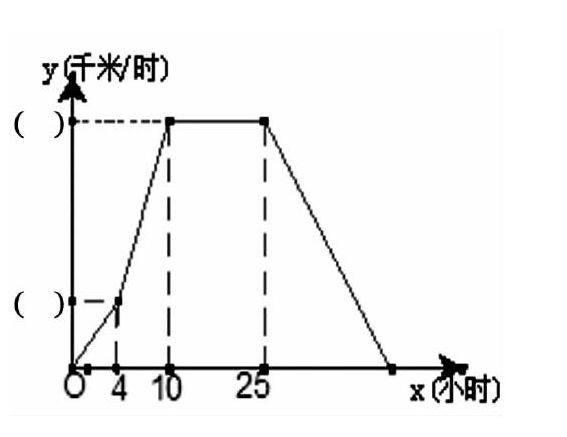
案例5：某氣象研究中心觀測一場沙塵暴從發生到結束的全過程，開始時風速平均每小時增加2千米/時，4小時后，沙塵暴經過開闊荒漠地，風速變為平均每小時增加4千米/時，一段時間，風速保持不變，當沙塵暴遇到綠色植被區時，其風速平均每小時減少1千米/時，最終停止.結合風速與時間的圖象，回答下列問題：

1.在y軸（ ）內填入相應的數值；

2.沙塵暴從發生到結束，共經過多少小時？

3.求出當x≥25時，風速y（千米/時）與時間x（小時）之間的函數關系式。

？笙 編輯：謝穎麗