大學數學分層教學的理性思考

熊文耀 崔海建

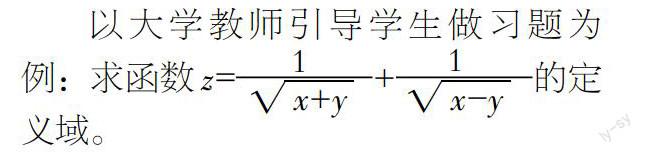
摘 要：學生和市場的需求都提出大學數學教師必須以分層教學的思路開展教學。本次研究提出了大學數學教師要在教學中具備分層教學的意識，掌握分層教學的方法，引導學生自主學習，分層拓展知識。

關鍵詞：高等數學；數學教學；分層教學

在傳統的數學教學中，人們認為大學數學教學的目的是讓學生學習的成果能夠滿足教學大綱的要求，但是這種統一化的教學標準已經不符合現代化的人才要求。從學生的角度來說，每個學生的資質不同，志向不同，他們希望能依照自身發展的情況學習數學知識；從市場的角度來說，市場對人才有復合的要求。市場既需要擁有一定基礎和文化、具有專業知識的人才，也需要具備高級知識儲備，能以宏觀的角度看待問題的復合型人才。

1.以分層的教學思路決定教學目標

不同層次的學生有不同的學習目標。第一個層次的學生，他們僅僅只想學習基礎的大學知識。他們學習數學知識的目的只是打好一定的數學基礎，以便學習相關的專業知識。大學數學教師要以數學課本為范圍，引導學生熟悉數學課本中的知識；第二個層次的學生，他們對數學有一定的興趣，他們希望能在現學數學知識的基礎上，稍微學習自己感興趣的數學知識。大學數學教師要引導這類學生理解數學課本中的知識，培養數學學習興趣；第三個層次的學生對數學知識有濃厚的興趣，他們能自主地把數學知識與其他領域的知識結合起來。大學數學教師要引導學生學習課本中的知識，結合他們的研究興趣引導他們拓展知識。

以大學教師引導學生做習題為例：求函數z=—+—的定義域。

這一題就是最基礎的大學數學習題，只要學生研習過課本，熟悉這一數學概念，就能解決這一道習題。只是對第一層次的學生來說，這類習題是他們學習的重點；對第二層次的學生來說，這道習題是他們學習的基礎；對第三個層次的學生來說，他們能輕松地解答出這類習題。

大學教師引導學生決定學習的目標，學生才能夠找準自己需要學習的范圍，有效率地學習數學知識。

2.以分層的教學思路決定教學方法

學生的資質有差異性。有的學生空間想象力很強，他們能夠以宏觀的高度思考非常抽象的問題；有的學生形象思維能力強，他們只有眼前出現了具體的事物，才能根據這些事物去摸索相關的規律；有的學生邏輯思維能力比較強，他們能夠用由此及彼的方式把知識和知識串聯起來。數學教師要根據學生的特點引導學生用不同的方法學習知識。

比如，對形象思維能力較強的學生來說，他們看到數學課本中的知識就覺得很復雜，找不到學習的方向。這并不意味著這類學生學不好數學知識，只是對這些學生來說，他們很難依靠研究數學課本或研習數學習題來學好數學知識。因為數學課本和數學習題既沒有直觀的圖形，也沒有詳細的數學知識描述的過程，形象思維能力較強的學生在學習這類知識時無法發揮優勢，學習的效率就會不高。大學數學教師可鼓勵學生去看大學數學的公共課程，或者與之相關的數學軟件。在公共課程中，大學數學教師會詳細地分析大學數學問題的難點，將它們用PPT的方式展現出來，詳細地說明這些數學問題的解答過程。形象思維能力較強的學生通過接受語言信息、圖片信息、多媒體信息，能夠理解大學數學課本中講述的內容，他們就能夠迅速地掌握大學數學課本中的數學知識。

3.以分層的教學思路決定教學拓展

部分學生學習了大學課本中的知識以后，希望學習與之相關的知識，拓展數學知識結構。有少部分數學教師用引導學生做習題的方法拓展學生的知識結構。一道又一道枯燥的習題讓學生找不到學習的重點，他們做了大量的數學習題以后，學習的熱情慢慢消失了，以后不再愿意自主地拓展數學知識。大學數學教師要意識到，要讓學生有效地拓展數學知識，就要用分層的教學思路引導學生找到知識拓展的方向。

以引導對物理知識感興趣的學生為例，數學教師可引導學生學習這樣一個公式：靜電場的場量和源量分布滿足二維拉普拉斯方程。即：▽2Φ（x，y）=

—+—那么這一公式是如何應用的？應用在哪些領域呢？有一名學生經過教師的引導，發現大學數學與物理知識有這么緊密的聯系，于是他對數學知識在物理知識中的應用產生興趣。這名學生經過思考以后，提出電磁場中的復電位能應用到這一知識。

這名學生認為如果f（z）=u（x，y）+

iv（x，y），那么可得：

—+—=0；

—+—=0；

學生解析到此以后，他認為可結合柯西—黎曼條件的思路解決數學問題，即可得：

—=—，—=—

解之可得：

E（z）=-—+i—=-—；

最終可得復電位的條件為f（z）。

大學數學的知識被廣泛應用在生物學、化學、物理等科學領域中，數學教師可結合學生的興趣愛好引導學生拓展數學知識。當學生發現數學知識與他們感興趣的領域緊密結合時，他們便會自主地拓展數學知識，完善數學知識結構。

大學數學教師在開展數學教學時，不能一味地要求學生學好數學課本中的知識，而要用理性的態度看待學生的層次性，用分層的方式引導學生學好數學知識，從而提高數學教學的效率。

參考文獻：

[1]蔣青松.大學數學課程考核中構建多元化考核評價指標體系的思考[J].課程教育研究，2015（13）：27—28.

[2]胡建根.高等數學教學中隱性分層合作教學的應用[J].江西教育，2015（04）：18—19.

（作者單位：南昌工學院）