巧妙設計數學練習?撞擊學生思維火花
劉愛玲
摘 要:課堂練習是鞏固知識、形成技能、發展思維、培養學生創造能力的重要途徑。好的教學策略,優化的課堂訓練,不僅能提高教學效率和教學質量,還能開發培養學生的創新能力,提高學生思維能力。課堂練習的設計應從趣味性、對比性、層次性、開放性、生活性的角度設計練習,練習設計要達到最優化,以期發揮練習在課堂中的最佳效率。
關鍵詞:小學數學;課堂練習;巧妙設計
一、設計趣味性練習,促進學生積極思維
愛因斯坦有句名言:“興趣是最好的老師。”說明興趣對學習有著神奇的內驅動作用,能變無效為有效,化低效為高效。心理學研究也表明,當學生對某一學習內容的練習活動產生濃厚的興趣時,他就會積極思考,大膽探索,從而優化自己的認知活動,促進學習。而趣味性的練習是培養學生學習興趣的重要方法之一。因此設計練習時應注重題目的趣味性,使學生在愉快中獲得知識,提高教學效率。例如,學習了“長方形、正方形的認識”后,我設計了課尾練習設計“猜猜邊長是多少”。
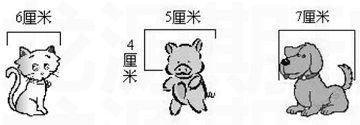
(1)小貓后面藏了一個正方形,可以看見的這條邊是6厘米,小朋友,你們知道看不見的三條邊各是多少嗎?請說出理由。
(2)小豬后面藏的是一個長方形,可以看見的兩條邊分別是5厘米和4厘米,小朋友你能猜出另外兩條邊是多少嗎?請說出理由。
(3)小狗后面也藏了個圖形。這個圖形是個四邊形,四個角都是直角,周長是24厘米,其中一條邊是7厘米。你能想想它是什么圖形嗎?其他三條邊的長度又是多少呢?為什么?
這種趣味性練習,不僅培養了學生的興趣,還促進學生積極思維,又培養學生的數學表達能力。
二、設計對比性練習,啟迪學生創新思維
前蘇聯教育家烏申斯基說過:“比較是一切理解和思維的基礎,我們正是通過比較來了解世界上的一切。”顯然烏申斯基所強調的是一種思維能力,即比較思維能力。如在教完“較復雜的分數應用題”后,學生在解題時審題不夠細,對應關系找不準,如何讓學生認真過審題關呢?可設計如下練習。
(1)一根繩子長6米,用去2/3米,還剩多少米?
(2)一根繩子長6米,用去2/3,還剩多少米?
雖然只是一字之差,但解題方法和結果卻大不相同。可見審題的重要性,以后不用老師強調,學生就會自覺審題,養成良好的審題習慣,同時能讓學生在解題中發展學生的比較思維。
三、設計層次性練習,發展學生靈活思維
學生接受知識和鞏固知識的過程依照由易到難,由淺入深的學習規律,考慮到不同層次學生的學習差異,因此,在課堂練習的內容上有層次、要求上有差異。我一般將課堂練習分為幾個層次。
一類題面向全體學生,特別注意班級中的學困生,內容以本節課應掌握的基礎題為主。
二類題面向班上中等以上的學生,題目的設計力求有一定的難度,指向學生的最近發展區。
三類題面向班上學有余力的優秀生,內容在二類題的基礎上要有一定的發展,培養發散思維能力,鼓勵超前學習。
要求學生在完成規定層次的練習后還能帶著勝利的喜悅去做高一層次的練習。這樣做才能讓不同的學生在數學學習上得到不同的發展。如教學“簡單的平均數應用題”時,我設計如下幾個層次的練習,幫助學生鞏固深化所學的知識。
(1)列式并計算。小紅買來一本故事書,第一天看8頁,第二天看6頁,第三天看12頁,最后一天看10頁,平均每天看多少頁?
(2)只列式不計算,并說理分析。氣象小組在一天的2時、8時、14時、20時,測得溫度分別是13度、16度、25度、18度。求這一天的平均溫度。
(3)選擇算式,并說明理由。玩具廠生產玩具,第一天生產180個,第二天生產200個,第三天上午生產120個,下午生產100個,平均每天生產多少個?
下面的哪種解法哪個對?哪個錯?為什么?
(180+200+120+100)÷4
(180+200+120+100)÷3
(4)列式并計算,說明理由。哥哥和弟弟的平均身高是140厘米,已知哥哥身高是143厘米,弟弟身高是多少厘米?
以上幾個層次的練習都是圍繞總數、份數與平均數三個數量之間的關系來設計的。從易到難,從單一到綜合,從順向到逆向,題型多變,形式多樣。通過練習,學生不僅掌握了基礎知識和基本技能,還培養了靈活的思維能力。
四、設計開放性練習,挖掘學生創新思維
小學生由于知識及年齡的特點,往往反映出對問題的思考是單向的、一維的。因此,在數學課中,要經常設計一些開放式的練習題,強化訓練,發展學生創新能力,讓學生在知識的天空中自由翱翔,從中訓練他們思維的深刻性、發散性和創造性,讓他們主動地進行學習,加深對知識的理解和掌握,激發創造性思維。
例如,在教學“分數乘法”這一課時,我設計了下面練習:
有兩根同樣長的鐵絲,第一根用去3/8米,第二根用去3/8,哪一根剩下部分長一些?
這道題的結論不明確,必須要根據鐵絲原來的長度進行分析,我們不妨假設其原來的長度為a米。①當a>1時,a×3/8 > 3/8米,故第一根剩下部分更長一些;②當a=1時,a×3/8 =
3/8米,故兩根剩下部分長相等;③當a<1時,a×3/8 ?< 3/8米,故第二根剩下部分更長一些。
又如 1/3×( ? )=( ? )×1/5 = 9×( ? )。
通過練習、比較,當它們的乘積為1時,答案最簡便。這樣就開闊了學生的思路,培養了學生的綜合能力,挖掘了學生的創新思維。
五、設計生活性練習,培養學生發散思維
《數學課程標準》指出:“老師應該充分利用學生已有的生活經驗,隨時引導學生把所學的數學知識應用到生活中去,解決身邊的數學問題,了解數學在現實生活中的作用,體會學習數學的重要性。”因此,數學練習的設計要聯系生活實際,讓學生把課堂上所學的數學知識運用于解決實現生活中的問題,讓學生有成功體驗,使學生感受到數學與日常生活的密切聯系,從而激發學生學習數學的興趣與動機,充分調動學生學習數學的積極性和主動性。
學了時間單位和長度單位后,可設計修改病句的練習:2015年2月29日,我到南京姑媽家。晚上我從永安出發,到南京可遠了,足足有1000毫米,從9:00到早上6:00,坐火車用了6小時。姑媽來火車站接我,她還是那么年輕,身高162米,體重50克。見到姑媽我真高興。
通過這樣的練習,不但能增添課堂的氣氛,而且能加深學生對數學的理解,學以致用,有很大好處,有效地促進了學生的發散思維。
總之,在數學教學中,巧妙設計發展性練習,積極創造條件,以學生發展為本,喚起學生的創新意識,培養學生的創新精神,提高學生的創新能力,使學生能時時撞擊出創新的思維火花。
(作者單位:福建省永安市實驗小學)

