小學數學教學中數形結合思想的滲透
林慶壽
摘 要: 數形結合思想是數學教學中重要的思想,它通過數與形的相互轉化,將抽象的數學語言與直觀的圖形結合起來,以形助數,以數輔形,化繁為簡,化抽象為具體,開拓學生的解題思路,使邏輯思維與形象思維完美地統一起來,促進學生有效地解決數學問題。
關鍵詞: 小學數學教學 數形結合 滲透
數形結合思想就是通過數和形之間的對應關系和相互轉化來解決問題的思想方法。“數”與“形”是數學研究的兩個基本對象,利用“數形結合”方法能使“數”和“形”統一起來,借助于“形”的直觀理解抽象的“數”、運用“數”細致入微地刻畫“形”的特征,達到直觀與抽象相互配合、取長補短,從而順利、高效地解決數學問題。下面結合我的實際教學談談如何在小學數學教學中滲透數形結合思想。
一、備課時,挖掘數形結合思想適時滲透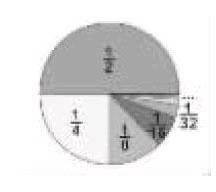
贊可夫說:“教會學生思考,這對學生來說,是一生中最有價值的本錢。”教會學生思考就是要教會學生掌握數學思想方法。小學常用的數學思想方法很多,而數形結合思想具有數學學科的鮮明特點,是解決許多數學問題的有效思想。因此,備課中,我們要深入挖掘教材中蘊含的數形結合思想,設計能有效引導學生經歷知識形成過程的教學方法,讓學生在觀察、對比、分析、抽象、概括的過程中領悟數學知識蘊涵的思想。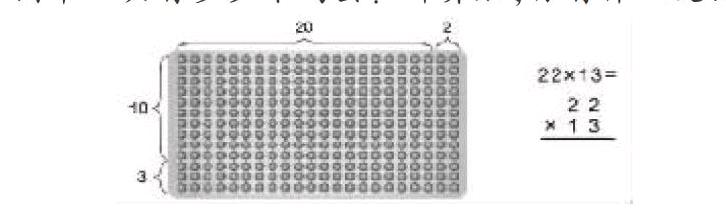
如教學六年級上冊第八單元“數與形”這道題有無數個數相加,用學生現有的知識根本無法直接計算。備課中,教師應考慮到教學時要先引導學生觀察加數的特點:每一項的分子都是1,每一項的分母都是它前一項分母的2倍;也可以說第幾項的分母就是2的幾次方,第n項就是2的n次方。接著引導學生聯想到分數的計算可以用直觀圖表示,然后教師可以構造一個長度或者面積是1的圖形(如圓形或正方形),如下圖所示。先取它的一半作為二分之一,再取余下一半的一半作為四分之一,如此取下去……當取的次數很大很大時,余下的面積就非常小了,引導學生觀察圖形,想象當取的次數趨向于無窮大時,余下的部分就趨向于0,因而最后取的線段長(面積)是1。所以這題的得數是1。本題結合數軸和圖形建立了一一對應關系,真正做到以形助數,幫助學生理解算理,在理解算理的基礎上掌握計算方法,正所謂“知其然,知其所以然”。數與形的結合讓學生進一步感受到“化數為形”的直觀、形象、簡潔的特點,在這一過程中,學生也體會到推理和極限的思想。
我們應該充分根據孩子們的認知規律,在教學過程中適時滲透數形結合思想,培養他們的數學思維能力。備課時,教師就要深入研究教材,吃透教材編排的意圖,有效滲透數形結合思想,彰顯數學學習的價值。
二、課堂上,巧用數形結合建構模型
“數無形時少直觀,形少數時難入微”,利用數形結合,可以使某些抽象的數學問題直觀化、生動化,使問題化難為易、化繁為簡,激發學生學習興趣。在教學中那些學生覺得難以理解的易出現錯誤或混淆的內容,教師可充分利用“形”,把抽象的問題變得直觀、形象,豐富學生的表象,引發聯想,引導學生探索規律,建構解題模型。
如我在教學五年級上冊“植樹問題”時,先以人人都有的手為素材,讓學生伸出手觀察,從而認識“棵樹”與間隔數,滲透一一對應思想,為新課學習做好鋪墊。接著出示例題:同學們在全長20m的小路一邊植樹,每隔5米栽一棵(兩端要栽),一共要栽多少棵樹?我先放手讓學生自主探究,學生有的通過實踐操作把牙簽插在長條形橡皮泥上模擬種樹,有的畫線段圖分析。接著我讓學生在線段圖中結合數字分析:20里面有4個5,每增加5米種1棵,加上開頭的1棵,一共是5棵。這樣加強了數與形之間的聯系,化解了難點,從而得出解題模型,兩端都種:棵數=間隔數+1。學生用前面探究的經驗和方法繼續自主探究,很快得出植樹問題的另外兩種解題策略,只種一端:棵數=間隔數,兩端都不種:棵數=間隔數-1。
通過這樣的“數形結合”,學生以后解題時看到算式眼前就會出現圖形,見到圖形就能聯想到算式,對后面的練習就迎刃而解了。本課借助實際操作和畫線段圖的方法,正確理解植樹棵數與間隔數之間的關系,化抽象為具體,使學生深刻理解題意,自主探究出解題模型,學生的思維發展有了憑借,數學思想方法真正得以滲透。
三、練習中,滲透數形結合提高能力
課堂練習是小學數學教學的重要組成部分,是學生數學學習必不可少的重要環節,是學生掌握知識,形成技能,發展智力的重要手段。因此,教師引導學生掌握理解課堂練習題是十分重要的。有些題目利用數形結合的方法,能讓學生表象清晰,記憶深刻,對算理理解透徹,有利于提高學生的解題能力和思維能力。
例如教學三年級下冊47頁第1題時,我先引導學生觀察點子方陣圖,每行有22個雞蛋,求13行有幾個雞蛋。把22分成20和2,13分成10和3,先算2×3=6,20×3=60,2×10=20,20×10=200(結合每步的算式在圖中圈出對應的部分)。也就是說點子圖由4部分組成,200+60+20+6=286。由此引導學生結合點子圖完成右邊算式的筆算。這樣借助直觀的圖形學生理解了兩位數乘兩位數的算理,掌握了算法。計算完成后,還可以讓學生看著算式解釋圖形,兩者結合,真正做到“以形助數,以數解形”。
下圖中一共有多少個雞蛋?計算后,你有什么發現?
數與形是緊密聯系、相輔相成的。在數學教學中滲透數形結合思想,不僅能提高學生分析能力、思維能力及解決數學問題的能力,還深深地影響著學生今后的數學學習和知識的應用。數形結合思想不可能一朝一夕形成,它需要長期滲透才能逐步讓學生掌握。因此,教師要做教學的有心人,在具體的教學中有目的、有計劃、有系統,適時適度地滲透,讓數形結合思想始終貫穿在學生的數學學習過程中,成為一種有意識的教學活動。只有這樣,數形結合思想方法的教學才能落到實處,數形結合思想才能作為學生學習數、運用數學和創造數學的有力工具。
參考文獻:
[1]劉加霞,主編.小學數學課堂的有效教學.北京師范大學出版社,2008.6.
[2]教育部.義務教育數學課程標準.北京師范大學出版社,2011.
[3]王永春.小學數學與數學思想方法.華東師范大學出版社,2014.

