高中數學概率統計模塊的教學研究

管琴

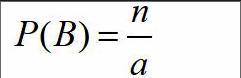
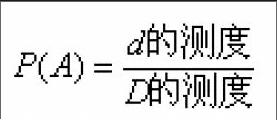
摘要：掌握概率統計模塊知識，可以對復雜的實際問題進行解答，進而解決數學問題。從目前高考題的構成來看，這部分內容和知識的占比也在不斷增加，故可以說當前概率統計知識已經在高中數學教學中占據了不可替代的地位。學生在掌握了概率統計模塊知識的前提下，可以對很多實際問題進行解答，這樣有效的提升了學生的解題能力。另外，該部分知識還能有效的提高教學質量，促進教學效果的提升。最為重要的一點是，這部分知識的教學還能有效的激發學生進行數學學習的興趣，所以本文的研究可以說是意義和作用巨大的。

關鍵詞：高中數學；概率；統計；教學

高中學生通過課堂知識來進行概率統計的學習，然后將其應用在日常生活當中，一方面能夠激發起學生熱愛數學的熱情，另外一方面還能夠幫助學生打開視野。伴隨著新課標的實施和我國高中數學的改革，概率和統計模塊知識的內容就被有選擇性地劃定為必修的內容，但是其作為高中數學教學當中基礎性的必修內容，本模塊的內容安排上與以前有較大的差異。

一、高中數學概率統計模塊教學案例

人教版幾何概型內容進行教學設計：

設置問題

復習回顧問題1

古典概型的特征：

實驗結果中每一個基本事件發生的可能性都是相同的

所有的基本事件只有有限個

復習回顧問題2：

古典概型的計算方式：

例如在某一實驗當中，假定等可能事件數量為a個，那么所有的等可能事件出現概率將全部是。假定在事件B中，其中的等可能事件為n個，所以B事件出現的概率將是

復習回顧問題3：

從{0，1，-3，-4，6，-2}選出任何的數，比0大的概率是多少？這種類型的數學問題，主要是對古典概型知識的再次輸入，使得學生在解決實際問題時，能夠自己獨立解答，同時，也可以很好的變換到，引入幾何概型的知識。

在區間（-5，2）中隨機的抽取一個數，那么小于0的概率將是多少呢？在上一個題的基礎之上，可以讓學生獨立進行思考完成解答。

源于對實數知識的理解，多數學生能夠獨立完成，還可以解釋清楚。我在課堂上的講解為：在區間內任意取一個數，對應數軸上的一個點，無數個點構成了線，這個過程體現了具體實驗結果對應數，數對應點，點構成線，最終完成基本事件與點的對應，進而通過幾何度量實現對幾何概型有關額外難題的有效解決。同時，使得無限結果體現得具體且直觀，是培養學生抽象思維的好時機。接下來，學生能通過自主性的探究來有效的解決以下問題，即實際問題1和實際問題2。逐步達到對幾何概型的認識，聯系古典概型，對比性地加深理解。

實際問題1：

一根木棍，這根木棍長6米，如果在這根木棍任意處砍斷，那么砍斷的這兩根木棍的長度小于2的概率是多少？從之前的數學問題，再過渡到實際問題，這對學生來說雖有有難度，但又非常重要，有利于培養學生建立數學模型。

實際問題2：

在射擊比賽中，靶面的中心的直徑為12.2厘米，靶面的直徑為122厘米，靶面分環有五個顏色，由內到至外顏色依次為金、紅、藍、黑、白，中間的顏色是金色。比賽中，射中任何一點的可能性都是一樣的，那么金色被射中的概率是多少？這是從線過渡到面，增加了一個維度。

二、數學構建（由學生完成）

幾何概型的特征：在本實驗當中，所有的基本事件出現的概率都是一樣的，基本事件有無數個。

幾何概型的運算方式：

1.在本實驗當中，我們將全部結果組成的可度量區域叫做D區域，在其中某一個事件A中，結構構成的可度量的區域稱為d。

2.測量的有可能是面積，也有可能是體積，還有可能是長度等等。

這部分可以完全由學生總結，教師加以適當補充和完善。之后，以實驗結果對應的區域會出現不同類型區域出發，設置問題，有學生探究，并小組合作完成講解。

在這次教學設計中，為了使得其對古典概型的理解更深入，另外還需要對幾何概型有充分的人事，本文將研究的重點側重在了二者的區別方面，以及有什么內在聯系上，有層次的設置情景，設置問題，引導學生完成建構過程，這樣使學生清楚了幾何概型的意義。

三、高中數學概率統計模塊教學存在的問題及對策

當前高中數學概率統計模塊教學主要存在著思維定勢上存在偏差、對概念不夠重視、概率問題的錯誤直覺、教師對學生缺乏正確的認識幾大問題，而要解決這些問題，那么教師就需要注重對概率統計核心內容進行理解、重視對概率模型的理解應用、注重培養學生正確的直覺、突出統計思維、注重案例、數據的收集、加強知識間的相互聯系。例如以獨立重復試驗為例：把一枚均勻的硬幣隨意拋出，如果拋出1000次，那么很多學生可能認為會出現500次正面，也就說，出現這樣結果的概率是很大的，但其實，通過我們的運算，出現這種結果的概率只有9%。把一枚均勻的硬幣拋出十次，每次都是背面朝下，那么進行第11次試驗時，結果會是哪一面朝下呢？有的同學認為是正面，而實際上，不論之前做了多少次試驗，進行第11次試驗的時候，其都是獨立進行的，因此，其得出的結果，無論是正面朝下還是反面朝下概率都相同，都是，這次試驗得出來的結果，與之前試驗得出來的結果之間沒有什么關聯。這樣的過程就能夠讓學生錯誤的理解，親自進行感受隨機現象的試驗，把得出的數據進行記錄，把試驗的出來的結果，與事先之前想到的可能發生的結果兩者進行比較。

總結：作為一線教師對概率有關知識的理解和掌握將會在很大程度上影響到學生對該知識的學習，教師的教學不能只向高考和教材看齊，還應該讓學生認識到概率統計所具有的現實意義，在此基礎上，使學生的能力得到發展，學生的思維不斷開闊。

參考文獻：

[1]張馨心.高中數學概率統計的教學設計研究[D].遼寧師范大學.2011。