從折紙活動中淺談學生創造性思維的培養

馮世豪 盧德均

[摘 要] 勾股定理是初中數學一個重要的概念，筆者通過折紙活動中的數學經驗，用折紙設計了一堂綜合實踐課，以探究勾股定理的多種證明方法，并在此過程中淺談學生創造性思維的培養.

[關鍵詞] 折紙；勾股定理；創造性思維

引言

《初中數學課程標準》（2011版）明確指出：“創新意識的培養是現代數學教育的基本任務，應體現在數學教與學的過程之中. 學生自己發現和提出問題是創新的基礎；獨立思考、學會思考是創新的核心；歸納概括得到猜想和規律，并加以驗證，是創新的重要方法. 創新意識的培養應該從義務教育階段做起，貫穿數學教育始終. ”現代折紙主要運用于科技、數學、教育、藝術四大領域，數學課上的折紙是學習意義上的折紙，能夠為學生營造一個手腦并用的學習環境，能激發學生對數學的學習興趣，能引發學生數學思考，能鼓勵學生進行創造性思維，這也是筆者將折紙作為探索勾股定理教學素材的原因之一.

教學設計

1. 教學分析

剛升入初中的學生已掌握了一些簡單幾何圖形的性質，為了增強學生的學習興趣，提高學生對知識的應用能力，筆者將“用折紙來探索勾股定理”作為本堂課的內容.

2. 材料準備

為了方便學生觀察，選取邊長為15 cm且正、反兩面顏色不同的雙面正方形紙作為本節課的材料.

3. 學情分析

根據選材內容，將授課對象定為初中生. 在本堂課之前，學生掌握了一些簡單幾何圖形的基本性質，以及求簡單幾個圖形的面積公式.

4. 教學目標分析

《數學課程標準》（2011版）將綜合實踐課的教學目標分為知識技能、數學思考、問題解決、情感態度四個維度.

知識技能：在掌握正方形及等腰直角三角形性質的基礎上理解折疊過程中的數學原理.

數學思考：通過問題驅動下的折疊與組拼過程，讓學生學會獨立思考，培養探索精神.

問題解決：從組拼出來的圖案中發現勾股定理，運用兩種求正方形面積的方法來解決簡單的實際問題，增強應用意識.

情感態度：在問題驅動下的折疊與組拼過程中，提高動手操作能力，發散思維，體驗成功的樂趣.

5. 教學重難點分析

教學重點：勾股定理內容的掌握.

教學難點：勾股定理的推導過程.

6. 教學方法

合作式探究.

7. 教學過程設計

【探究問題一】

師：同學們，對于正方形，我們已經非常熟悉. 我們知道，正方形的四條邊相等，四個角都為直角. 那么，一張正方形紙，能否通過折疊分解為四個形狀和大小都相同的正方形？同樣地，能否通過折疊，分解成四個形狀和大小都相同的長方形？

解答過程 將正方形ABCD的對邊AD，BC重合，可得一個長方形. 在此基礎上，將長方形兩條短邊重合，展開后的折痕如圖1；將長方形兩條長邊重合，展開后的折痕如圖2.

設計意圖 熟悉正方形的性質，培養學生的歸納和觀察能力.

【探究問題二】

師：我們知道，等腰直角三角形的頂角是直角，兩條腰相等. 同樣的，正方形紙能不能通過折疊分解成四個形狀和大小都相同的等腰直角三角形？能否分解為四個形狀和大小都相同的一般直角三角形？請同學們嘗試思考多種折法.

解答過程 將正方形ABCD中不相鄰的兩組頂點A和C、B和D分別重合折疊，得圖3；正方形ABCD中兩對邊AB和CD重合，展開后沿AE和DE（E為BC的中點）對折可得圖4.

設計意圖 熟悉等腰直角三角形的性質，發散學生的思維，培養學生的操作能力.

【探究問題三】

師：下面我們增加一點難度. 能否將正方形紙分解為形狀和大小都相同的兩個梯形呢？在此基礎上，能否將正方形分解為四個形狀和大小都相同的四邊形呢？你能想到哪些好的折疊方法？

解答過程 首先得到正方形的中心O，過點O任意折一條直線GH，展開得圖5；在圖5的基礎上，將點G和點H重合對折，展開后得圖6. 還可以發現，得到的四邊形有兩個角是直角.

設計意圖 培養學生的探索精神，創設發現勾股定理的情境.

【探究問題四】

師：在圖6中，分別沿FH，HE，EG，GF折疊，你發現了什么？

解答過程 我們發現四個形狀、大小都相同的直角三角形圍成了一個正方形（圖7）. 三國時期吳國的數學家趙爽創制了一幅“勾股圓方圖”，用數形結合的方法，嘗試對勾股定理做理論證明，這幅圖就是著名的“趙爽弦圖”. 趙爽的證明為中國古代以形證數、形數統一、代數和幾何緊密結合的獨特風格樹立了一個典范.

設計意圖 構建“趙爽弦圖”.

師：如圖8，我們設小直角三角形的直角邊的長分別為a，b，斜邊長為c，用兩種方法計算正方形EHFG的面積，你發現了什么？

解答過程 c2=（b-a）2+4×ab=a2+b2.

設計意圖 探究勾股定理的證明過程.

【探究問題五】

師：請嘗試將翻折過來的四個形狀和大小都相同的直角三角形剪下，在另外一張同樣大小的正方形紙上組拼兩個長方形，并讓余下的空白是兩個正方形.

解答過程？搖 如圖9.

設計意圖 培養學生的探索精神.

師：同樣，我們還可以把四個形狀和大小都相同的直角三角形拼成圖7的形狀，如圖10. 設小直角三角形的直角邊的長分別為a，b，斜邊長為c，比較圖9和圖10中白色正方形的面積，你發現了什么？

解答過程 由圖11和圖12可得c2=a2+b2.

設計意圖 通過兩幅圖空白正方形面積相等，發現勾股定理，培養學生的觀察、推理能力.

【探究問題六】

師：想一想，對于圖10，你同樣能推導出勾股定理嗎？你還能想到用其他的方法來證明嗎？

解答過程 如圖13，設小直角三角形的直角邊的長分別為a，b，斜邊長為c，根據正方形ABCD面積的兩種不同求法來推導公式，即正方形ABCD的面積=（a+b）2=ab×4+c2，整理可得c2=a2+b2.

設計意圖 培養學生的發散思維，加深學生對勾股定理的記憶.

思考：你還能想到證明勾股定理的其他方法嗎？

【附：其他方法證明勾股定理】

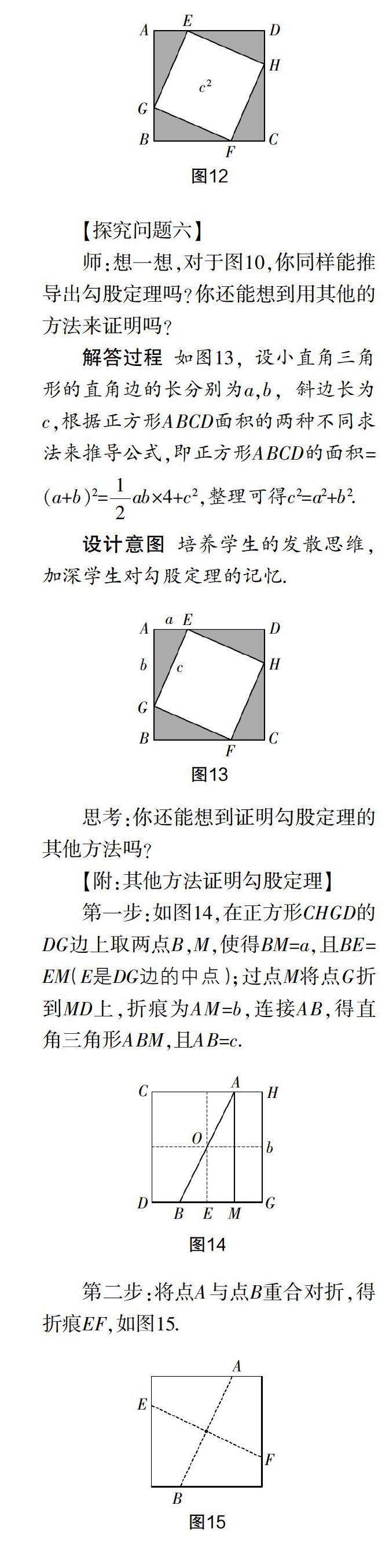
第一步：如圖14，在正方形CHGD的DG邊上取兩點B，M，使得BM=a，且BE=EM（E是DG邊的中點）；過點M將點G折到MD上，折痕為AM=b，連接AB，得直角三角形ABM，且AB=c.

第二步：將點A與點B重合對折，得折痕EF，如圖15.

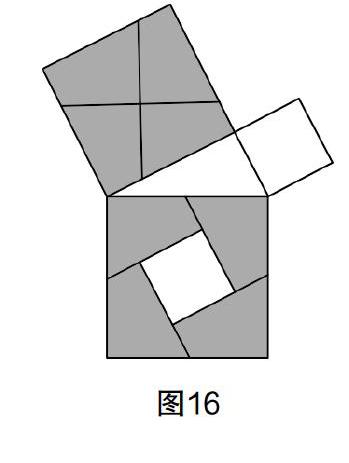
第三步：沿折痕EF和AB剪成四個全等的四邊形，按圖16拼圖便可得到勾股定理.

如何培養學生的創造性思維

美國著名心理學家、美國心理學會會長吉爾福特對于創造性思維的研究具有深遠的影響. 他在“智力的三維結構”模型中提出了創造性思維. 他認為，創造性思維是指從給定的信息中產生新信息，其著重點是從同一來源中產生各種各樣的為數眾多的輸出. 創造性思維具有流暢性、靈活性、獨創性三個最主要的特征.

折紙作為一種教學工具用于數學教學活動中，引導學生觀察折痕所形成的邊角關系，幫助學生構建折紙拼圖活動與數學內容的聯系，培養學生的動手能力、觀察能力、想象能力和創造性思維能力. 下面，筆者從本節課出發，淺析如何真正培養學生的創造性思維.

1. 流暢性

流暢性是指在規定時間內產生有效圖形信息的個數. 我們說創造性思維流暢，指的是遇到問題時，心智活動少阻塞，多流暢，在短時間內能夠找到知識之間的多個聯系，能產生較多的可供選擇的解決方案. 本節課營造的是一種探究式課堂，課堂開始對一張正方形紙進行四等分，從正方形、長方形到等腰三角形、直角三角形，一直到梯形、一般四邊形，不僅為后面折疊“趙爽弦圖”埋下伏筆，更在于啟發學生思考一張正方形紙可以四等分為哪些圖形，能訓練學生的創造性思維.

2. 靈活性

靈活性是指在規定時間內產生有效圖形信息的種類. 我們說圖形創造性思維變通，是指遇到困難時能夠隨機應變，及時調整解題思路或解題方法，能從多個方向、多個方面思考問題，能產生多種不同類型的可供選擇的解決方案，能用不同類型的方法解決問題，或能得到不同類型的答案. 靈活性和流暢性的主要區別在于，提供選擇的方案、方法、答案的性質有所不同.

本節課可歸納為解決兩個大問題，一是將正方形紙四等分成多種圖形的折疊方法，二是探究勾股定理的多種證明方法. 筆者通過與某中學初中數學教師交流，在某班進行了一堂課的教學. 在與學生交流中發現，在第一個問題中，學生的折疊方法多樣，通過教師的引導，能夠思考正方形紙與目標圖形之間的關聯，并按照正方形點、邊、角之間的關系，平面幾何圖形的性質等數學知識去嘗試折疊；對于第二個問題，勾股定理的證法多樣，需小組合作探究、上臺展示、教師歸納總結. 這兩個問題的解答過程，都鍛煉了學生創造性思維的靈活性，總體上來說，整堂課達到了預期設想的效果.

3. 獨創性

獨創性是指在規定時間內產生新穎、獨特、有效信息的個數. 我們說圖形創造性思維獨特，是指在解決圖形問題時，能突破常規和經驗的束縛，用新的觀點、新的方法、新的思路解決問題，或得出新穎、獨特、稀有的答案，創造性成分中最重要的是獨創性. 對于創造性思維水平的測量，到目前為止，獨創性的測量一直是學術界的難點. 對于教師來說，在教學過程中多提出能真正啟發學生創造性思維的問題，多鼓勵學生積極思考，多留時間給學生思考，才能更好地進行師生互動，從而上好“探究型”課.

結語

林崇德先生說：“素質教育是以創新精神為主題的教育，學生不僅僅應該擁有學習的能力，更應該有實踐和創新的能力. 開展具有創造性的數學活動，能夠激發學生在數學學習中的創造力.”就本堂課而言，把幾何圖形的性質以及求面積公式等數學知識運用到折紙活動當中，不僅能將數學知識、思維方法遷移到應用實際問題當中，而且能讓學生形成學習新知識的能力，從中培養學生的創造性思維.