數(shù)學建模思想和方法融入中等數(shù)學課程的研究

王曉燕

摘 要：數(shù)學建模是解決數(shù)學問題的有效途徑。本文闡述了數(shù)學建模融入中等數(shù)學課程的優(yōu)勢，進行了相關的應用舉例，還探討了如何在中等數(shù)學課程教學中培養(yǎng)學生的數(shù)學建模思想。

關鍵詞：數(shù)學建模;中等數(shù)學;數(shù)學思維

在中等數(shù)學課程的教學中，我們經(jīng)常讓學生通過數(shù)學的方法去解決一些實際問題。這些實際問題可以被轉換成數(shù)學模型，這個轉換的過程就被稱為數(shù)學建模。數(shù)學建模為解決數(shù)學問題提供了新的思路和方法，在中等數(shù)學課程的教學中起到了重要作用。

一 數(shù)學建模融入中等數(shù)學課程的優(yōu)勢

（一）提高對問題的分析、解決能力

數(shù)學建模通過對數(shù)學問題進行抽象的、具有概括性的思維，對問題當中的有效信息進行提煉和重組，使學生可以尋找到解決問題的方法。鍛煉了學生在抽象思維、綜合分析、理解和組織語言方面的能力。

（二）提高篩選和獲取信息的能力

學生在尋找解決問題思路的時候會利用教輔材料、互聯(lián)網(wǎng)等渠道來獲取信息，在龐大的信息海洋中，如何篩選出符合自己要求的，有價值的信息，是對學生篩選和獲取信息能力的又一個考量。尋找解決問題思路的過程，就是他們再一次理解問題的過程。

（三）提高學生的合作創(chuàng)新精神

數(shù)學建模并不是千篇一律的，通過不同的思維方式和入手點，可以表現(xiàn)出不同的形態(tài)，最終變成不一樣的解題方法。學生在一次次利用數(shù)學建模思維去解題的過程中，培養(yǎng)了自身的創(chuàng)造性，學會了用新的視角看待數(shù)學問題。同時在課堂上，不同的數(shù)學建模思維也會給學生帶來新的想法，促使學生們不斷完善自我、不斷協(xié)調(diào)彼此。不僅鍛煉了學生的創(chuàng)新思維，而且提升了學生合作解決問題的能力。

二 數(shù)學建模在中等數(shù)學課程中的應用舉例

我們以具體的案例來研究數(shù)學建模思想和方法如何融入中等數(shù)學。

例題：對于某銀行發(fā)行的理財產(chǎn)品，有下列三種購買方案，您會按照哪一種方案進行購買？

方案一：自購買之日起單份每年可獲得收益20元;

方案二：購買之日單份可獲得收益5元，往后每一年可比前一年多獲得收益5元;

方案三：購買之日單份可獲得收益0.2元，往后每一年可比前一年多獲得一倍收益。

常規(guī)解題思路：由題可知，投資收益的多少與天數(shù)成正比，所以我們可以建立以投資時間作為自變量的投資收益模型，對比在某一固定時間點的投資收益增長情況，尋找問題的解決方法。

解：設第x年所得收益是x元，則收益可表示為

方案一：y=20（x∈N*），方案二：y=5x（x∈N*），方案三：y=0.2×2x-1x∈N*）

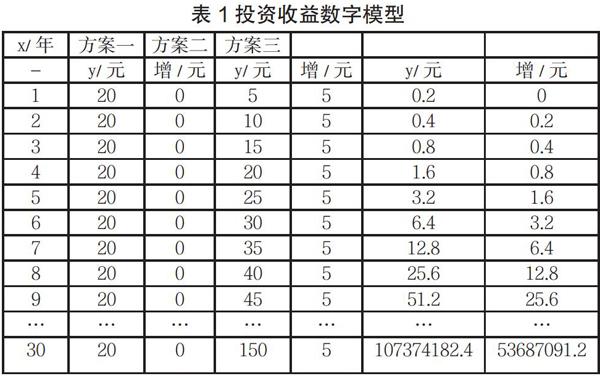
建模分析：我們先計算出三種方案收益的增長，如表所示：

通過分析三種方案的收益增長情況，我們可以發(fā)現(xiàn)開始幾年方案一的收益最多，從第5年到第8年的時候方案二的收益較多，當時間來到第9年的時候，方案三的收益最多。根據(jù)我們所列模型可以清晰地看出，方案一是一個常數(shù)函數(shù)，方案二和方案三都是增函數(shù)。函數(shù)的表示方法有列表法、圖像法、解析式法等多種，在解決函數(shù)問題的時候，我們也可以通過建立函數(shù)數(shù)字模型的方式來展現(xiàn)出一個更直觀的圖像，通過建立函數(shù)模型，我們可以直接反映出函數(shù)的一些性質(zhì)，把握增長情況。

在這道題中，我們通過設持有年數(shù)為自變量，建立了三個不同的函數(shù)圖像，從每年所獲得的收益來看，方案一在前四年的時候最多，方案二在第五年到第八年的時候最多，方案三在第九年以后最多。在教學的時候，當模型構建出來之后，我們還要引導學生繼續(xù)思考后面的細節(jié)問題。比如模型僅僅體現(xiàn)了每年的收益，我們在考慮理財收益的時候，還必須計算每一年所能得到的累計收益，以及三種不同投理財方式的投入成本，計算出每一種理財方式的凈收益，才能得出最終結果。

三 如何在中等數(shù)學課程教學中培養(yǎng)學生的數(shù)學建模思想

（一）加強對數(shù)學描述的訓練

數(shù)學描述對于數(shù)學問題的理解起到至關重要的作用，要在日常數(shù)學課程中加強對數(shù)學描述的訓練。專業(yè)性的數(shù)學描述并不局限于集合、代數(shù)式、函數(shù)關系、方程式等領域，對于生活當中的應用案例，也應該用數(shù)學語言進行描述。比如“有兩種轎車可供銷售，售價分別為3萬元和5萬元。如何證明在正常銷售的過程中可以獲得9萬元或者8萬元以上的任何整數(shù)萬元的收入”。簡化成數(shù)學知識為：“如何證明3的倍數(shù)與5的倍數(shù)之和可以是任何不小于8的自然數(shù)”。我們可以再簡化一下，將其變成標準的數(shù)學語言為：“存在非負整數(shù)m，n，對任意自然p≥8，都能得到p=3m+5n”。

（二）從傳統(tǒng)模型入手

學習數(shù)學建模思維和方法的時候，一開始就構建模型顯然難度頗大。可以從傳統(tǒng)的數(shù)學模型入手，掌握基本模型之后再進行創(chuàng)新。比如拋物模型，單色三角形模型，組合優(yōu)化中的中國郵路問題，圖論與幾何拓補中的七橋問題，還有細菌繁殖模型這種預測模型問題，都對數(shù)學模型的學習和構建起到良好的指引作用。對于以這些模型為基礎所創(chuàng)作的案例習題，學生在大量解讀和理解之后，將會掌握這些傳統(tǒng)的數(shù)學模型，訓練出基本的模型構建思維。

（三）數(shù)學結構

數(shù)學結構是一種關于現(xiàn)象特征的表示形式，與數(shù)學模型類似。數(shù)學模型的學習離不開對數(shù)學結構的研究，尤其是那些有助于建模的結構，教師應將其篩選出來，對學生進行重點教學。比如圖的結構，方程式的結構、數(shù)表和算法的結構等，這些是學生在日常數(shù)學課堂上無法學到的知識，因此在數(shù)學模型講座中需要進行講解和普及，讓學生能夠在此基礎上更好地構建數(shù)學模型。

（四）進行創(chuàng)新性思維訓練

對數(shù)學問題的綜合分析和解決問題都離不開創(chuàng)新性的思維，因此通過設計創(chuàng)新性思維訓練，能夠有效地提升學生創(chuàng)造數(shù)學模型的效率。創(chuàng)新思維的試題在歷年來的競賽試題中都存在，比如“在邊長一萬公里的正方形區(qū)域里存在40座城市，現(xiàn)在為其修建總長預計十一萬公里的道路，讓其中任意兩座城市都能夠有相連，請為其設計出至少一種方案。”學生在進行設計的過程中，會不斷嘗試和創(chuàng)建，結果不唯一，所經(jīng)歷的思維歷程也不一樣，能夠極大地鍛煉學生的創(chuàng)新性思維。再比如“如何用一個半圓形的畫圖工具讓一條過固定點的直線能夠垂直于半圓形工具（可沿著畫圖工具的邊緣畫直線）”。這道題限制了學生對于線條形狀、位置以及畫圖工具的選擇，要求學生克服困難給出符合規(guī)定的方案，不僅能夠鍛煉學生構建數(shù)學模型的能力，還能夠培養(yǎng)學生在解決困難時的良好心態(tài)。而這樣的能力和心態(tài)在解決數(shù)學難題時將會起到十分重要的作用。

（五）單獨建模問題訓練

教師可以針對學生的數(shù)學水平設計專門的建模問題，通過這些精心設計的建模問題，來讓學生對建模的方式展開討論研究，培養(yǎng)學生利用數(shù)學建模方法解決數(shù)學問題的思維。題目訓練可以讓學生學會舉一反三，將建模思路運用到其他的類似或者包含建模的數(shù)學問題當中。

例如“在一張邊長為十厘米的正方形紙板上裁剪出直徑為一厘米的圓形紙板，如何才能剪裁出最多的數(shù)量。”這是個看似開放，實則模型固定的問題，學生在對比各種不同的剪裁模型的同時，會不斷地靠近唯一的那個最優(yōu)解，并得到答案為106個。這就是直接用模型問題來訓練學生解決數(shù)學問題。

結語：

將數(shù)學建模的思想和方法融入中等數(shù)學課程中，通過對數(shù)學描述的訓練，對傳統(tǒng)模型、數(shù)學結構的學習，對創(chuàng)新性思維的訓練，不僅能夠幫助學生解決數(shù)學問題的難點，還能夠培養(yǎng)學生學習數(shù)學的興趣。在進行數(shù)學建模思想和方法的教學時也要循序漸進，幫助學生學會獨立構建模型。

參考文獻：

[1]白嚴旭.滲透建模思想，發(fā)展應用素養(yǎng)[J].中學數(shù)學，2019（22）：80-81+93.

[2]華蘭石.滲透數(shù)學思想方法，提高問題解決能力[J].數(shù)學學習與研究，2019（20）：35.

[3]李成杰.談初中數(shù)學教學中應用能力的培養(yǎng)途徑[J].才智，2019（33）：89.