探求數學的本質，追求數學的真諦，提高數學學習力

趙立新

[摘? 要] “K”型相似是解決大部分相似試題的基本圖形. 文章從“K”型相似問題說起，給出了這樣一個觀點：把知識點或同一類型的專題進行有效的整合，形成有一定梯度的題目，能讓學生做一題，會一類，通一片.

[關鍵詞] 中考復習;“K”型相似;數學本質;整合

中考復習時，數學教師會講解大量的中考題，但有時收效卻不是特別明顯，甚至有些是收效甚微的重復訓練. 筆者嘗試過多種類型和方法的實驗，最終發現，把知識點或同一類型的專題進行有效的整合，形成有一定梯度的題目，能讓學生做一題，會一類，通一片.

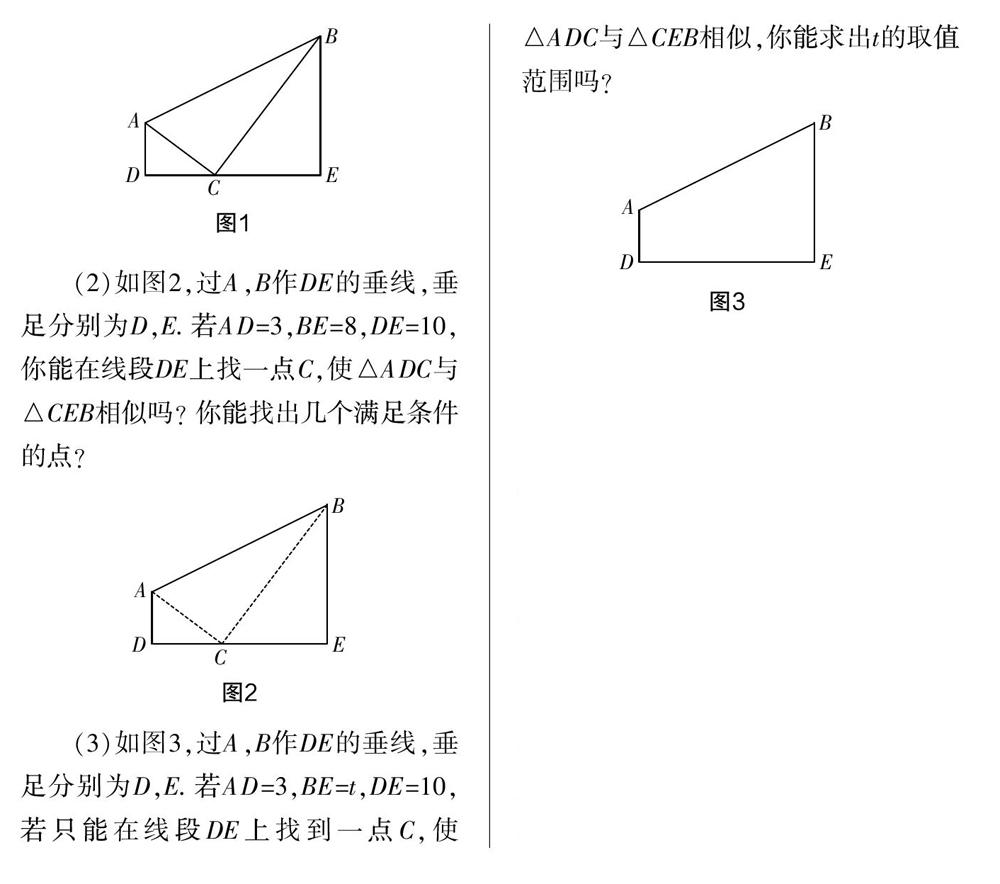
進行相似三角形的復習時，需要講解關于“K”型相似的問題，因為它在相似三角形里出現的頻率特別高，且是解決大部分相似類試題的基本圖形. 為了設計好試題的梯度，筆者設計了三個小問，如例1.

第（1）問是最基礎的相似，重點是讓學生知道它們為什么相似，為什么稱為“K”型相似，并讓基本圖形成為學生較好記憶的模型. 第（2）問是想讓學生區別“K”型相似（或稱為旋轉相似）與翻折相似的區別，這是為培養學生考慮問題的全面性而設計的. 第（3）問是在第（2）問的基礎之上建立的存在性問題. 由翻折相似的計算可知，它一定存在著一個點C滿足條件，而且它只有一個，也就是我們常說的翻折相似有且只有一個，而旋轉相似所得到的種類會有三種情況，即0個、1個或2個這樣的點C，所以條件中的那一個點C應該是由翻折相似得來的. 那說明旋轉相似是不存在的，于是可以據此求出t的取值范圍.

筆者教學例1時收到了較好的效果. 從后面的幾次測試反饋中也反映出學生對“K”型相似的理解還是比較到位的. 另外，教學第（3）問時，有的學生還進一步歸納出了“K”型相似存在的種類就是以AB為直徑的圓與線段DE的交點個數. 因為∠ACB=90°，從而以AB為直徑的圓一定經過點C. 由此可見，學生的分析非常準確，這樣更有利于他們對“K”型相似的理解.

1. 串成線，探求數學的本質

中考復習時，我們在追求“量”的同時，更應關注“質”的提升. 如果復習時能抓住一根主線，串聯起知識的體系，那學生對該知識的脈絡是非常清晰的. 當然，其也有利于學生對數學知識點的理解和掌握. 例如，設計二次函數的復習課時，有人通過“一圖一課”來展開，即以一個坐標系配以一個拋物線圖像為主線，添加適當的條件，讓學生自己提出問題并解決問題，逐步完成知識的覆蓋. 這種設計受到了學生和教師的一致好評. 實踐證明，教學效果也是非常明顯的，清晰的主線在幫助學生深入地理解二次函數的圖像及性質方面起到了重要的作用.

2. 連成片，追求數學的真諦

訓練學生的數學思維是數學課堂的重要任務之一. 如果用一根主線“串聯”起數學知識，那么，相應知識點的擴充和拓展就是“并聯”，其中有些擴充是對數學知識的深化，有些拓展是對數學知識的升華. 如講解例1時，由于學生想到了圓，所以筆者順勢拓展了一道與圓有關的運動變化試題. 該題既是對例1的延續和發展，也是對直角三角形與圓的關系的進一步揭示. 此外，還加入了動點探究，這更是進一步提高了對學生數學思想和方法的培養和發展，能讓數學知識點既串成線，也連成片，有利于揭示數學的真諦.

3. 結成網，提高數學學習力

數學課應注重“知識的形成過程”和“數學思想方法”的教學. “過程”是豐富多彩的，往往體現了數學的思想方法和價值;結論是重要的，但結論的獲得離不開過程. 因此，在數學復習課的教學中，我們應從條件出發，引導學生借助已有知識，縱向和橫向發展聯系，引導學生解答有關問題. 同時，啟發學生建立數學模型，并把數學問題“網絡化”，這樣不僅能讓學生長知識，更能讓學生長智慧，還能培養學生良好的思維品質.

布魯納指出：“掌握基本的數學思想方法，能使數學更易于理解和記憶. 領會基本的數學思想和方法是通向遷移大道的‘光明之路”. 在中考復習課教學中，我們要充分利用學生形象思維的特點，用“形”來解釋，從而引導學生將數與形結合起來，借助形象的圖形理解算理，提煉算法. 數學學習是有意義的建構學習，是在探索、交流、合作中完成的. 從這個意義上來說，數學教師的任務，就是引發學生思考，展現思維過程，指導交流與合作，完成數學知識的意義建構，讓學生從感知到認知，逐步深化知識之間的聯系，并在激活舊知識和不斷生長、發展的過程中，讓學生不知不覺地學會新知識. 這種橫縱聯系，不僅能促進學生的數學思維發展，還能更好地構建數學知識網絡. 這就是我們常說的“隨風潛入夜，潤物細無聲”.