掘思維“源頭”，引思維“活水”

陳云

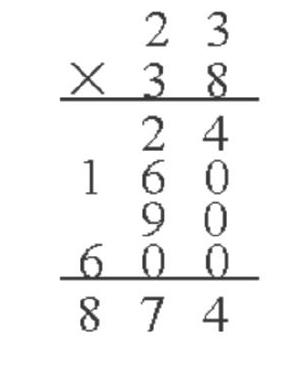
摘要：學校教育的首要任務(wù)是培養(yǎng)和提高學生的能力，而數(shù)學教學中學生能力的提高關(guān)鍵就在于數(shù)學思維的培養(yǎng)。問題“建模”是數(shù)學思維的基本形式，這個從具體的、熟知的生活情境中提煉、抽象、概括出“模式”的過程，能讓學生的比較、分析、抽象、概括等數(shù)學思維得到有效訓練。活動“內(nèi)化”是數(shù)學思維的重要內(nèi)涵，也就是要在教學中通過“同化”“順應(yīng)”使新知和已有認知結(jié)構(gòu)發(fā)生聯(lián)系，從而達到對新知的“內(nèi)化”。策略“化歸”是數(shù)學思維的本質(zhì)要求，長期堅持，學生的觀察、猜想及邏輯論證等能力都會有所提高。

關(guān)鍵詞：數(shù)學思維;問題建模;活動內(nèi)化;策略化歸

數(shù)學思維能力僵化現(xiàn)象在現(xiàn)代學生中是大量存在的，這與學生平時所受的思維訓練有很大關(guān)系。教師在教學過程中過分強調(diào)程式化，不斷給學生歸納各種題型，學生只會按部就班地解題，知其然不知其所以然，這樣的教學使學生的思維缺乏應(yīng)變能力，在面臨問題時就不能夠從多種角度進行思考，并迅速建立起自己的思路，真正做到舉一反三。如何更好地培養(yǎng)學生的數(shù)學思維能力？本文從數(shù)學思維的形式、內(nèi)涵、本質(zhì)要求三個方面對此進行闡述。

課程改革十余年，在探索前行中，仍有一些現(xiàn)象需要審視。在教學對象上，同一起點的學生由不同的教師教，思維存在較大的差異;在教學效果上，重負低效、輕負高效反差明顯;在教學追蹤上，高分低能、越學越差的現(xiàn)象仍有發(fā)生……如何有效凈化滋生這種現(xiàn)象的土壤，掘思維“源頭”，引思維“活水”呢？這就要求耕耘在一線的老師不僅要了解數(shù)學教學內(nèi)容本身的規(guī)律和含義，還要切實樹立整體和長遠的觀念，不斷地挖掘數(shù)學思維的素材，尋找培養(yǎng)數(shù)學思維的切入點。只有這樣才能達到《數(shù)學課程標準》中所要求的：“讓學生親身經(jīng)歷將實際問題抽象成數(shù)學模型并進行解釋與應(yīng)用的過程，進而使學生獲得對數(shù)學理解的同時，在思維能力、情感態(tài)度與價值觀等方面得到進步和發(fā)展。”

一、問題“建模”是數(shù)學思維的基本形式

數(shù)學是“模式”的科學，數(shù)學教學不能僅僅讓學生單純地去探究某個現(xiàn)實情境中特定的、單一的問題，而要從“某個”“某種”過渡到“某些”“某類”，從而抽象為普遍的“模式”。其間從具體的、熟知的生活情境中提煉、抽象、概括出“模式”的過程就是問題“建模”，這是數(shù)學思維的基本形式。如在“分類”知識的教學中，針對低年級學生，教師會引入豐富的現(xiàn)實情境，從整理房間、整理書包入手：用學具代替物品分一分、擺一擺;把書包里的東西倒出來整理一下……這種鼓勵學生用“實踐”的方法去解決問題的方式是可取的，但如果就此收兵，學生獲得的就僅僅是單一的、淺表的分類結(jié)果。倘若此時改變情境，讓學生給花園里的花、森林里的動物、操場上的人分類……學生拿出學具，卻一臉茫然：“老師，我的學具不夠怎么辦？”“老師，我忘了帶動物卡片，這可怎么擺啊？”“老師，操場上又是老師，又是小朋友，這可怎么分呢？”……緣何學生的思維停留在初級的實踐階段，還是需要依靠老師的提示去擺一擺、圈一圈、連一連才能得出結(jié)果呢？如果在整理房間、整理書包后，教師及時引導反思：“你是如何整理的？”“整理時只有一種分類方法嗎？”“你用什么方式把分類的結(jié)果直觀、簡潔地表示出來？”……學生通過比較兩次整理活動，從中發(fā)現(xiàn)、總結(jié)出分類的思維程序：“我知道：整理時首先要確定分類標準。”“原來同一些物品可以有不同的分類標準呀！”“確定了標準，還要劃分出合適的類別呢。”“我喜歡用序號法表示分類結(jié)果，就是先給要分類的東西編上序號……”“我認為集合圖更直觀……”這些表述說明學生的思維超越了具體問題，上升到抽象的高度，從而在這些“分類”的不同問題中揭示出它們事實上具有相同或類似的數(shù)學結(jié)果。這時候，再出示后面的幾個問題，學生就不需要擺學具、圈圖畫，而能理性地進行分類了。在這個問題“建模”的過程中，學生不但獲得了分類的結(jié)果，更重要的是比較、分析、抽象、概括的數(shù)學思維得到了有效的訓練。

二、活動“內(nèi)化”是數(shù)學思維的重要內(nèi)涵

著名哲學家、兒童心理學家皮亞杰早就明確指出了“內(nèi)化”對于數(shù)學學習活動的特殊重要性。皮亞杰認為，新的知識只有納入到原有知識結(jié)構(gòu)中才能被吸收，同化和順應(yīng)是使新知識和已有認知結(jié)構(gòu)發(fā)生聯(lián)系的過程，也就是內(nèi)化的過程。例如，在“面積的計算”教學中，教師給出幾個不同大小的長方形，如何得到它們的面積？經(jīng)過上節(jié)課的學習，學生會想到去進行實際的操作（用1平方厘米的小正方形去鋪需要測量面積的幾何圖形），第一個圖形鋪一次，第二個圖形“依葫蘆畫瓢”再鋪一次，第三個圖形不厭其煩地又鋪一次……雖然這是一種方法，但思維層面始終停留于實際的操作，未能在頭腦中實現(xiàn)必要的重構(gòu)或認知結(jié)構(gòu)的重組。教師在教學中可否考慮：第一個圖形用小正方形“滿鋪”，這是學生的原有認知結(jié)構(gòu);第二個圖形換成稍大些的。“老師，我的小正方形不夠用了怎么辦？”“我的也是……”學生的認知因新出現(xiàn)的狀況而產(chǎn)生沖突，如何變通？“想一想，有沒有什么辦法，用你手中僅有的小正方形，甚至不用這些正方形，也能測量出這個長方形含有多少個1平方厘米？合作試一試，看哪個小組用的小正方形最少。”學生經(jīng)歷了反復討論及驗證后展示了不同的方法：“我是沿著長鋪一行，沿寬鋪一列，我們發(fā)現(xiàn)如果鋪滿是5行6列，也就是30個1平方厘米。”“我只用了一個正方形，就是拿這個正方形的邊分別去量長方形的長、寬，也能知道鋪滿是5行6列，所以得出的結(jié)果是一樣的。”“我們小組根本就沒用小正方形，我們直接用直尺量出了長是6厘米，說明能鋪6個邊長是1厘米的小正方形，再量寬……”此時學生已經(jīng)由“全鋪”過渡到了“巧鋪”“意鋪”，從多個“巧鋪”到單個“意鋪”，還在此基礎(chǔ)上通過直尺測量實現(xiàn)了由“面”向“邊”的過渡。像這樣，學生把外界所提供的信息整合到自己原有認知結(jié)構(gòu)內(nèi)的過程就是“同化”。接下來，不再鋪了，老師隨意報出一組長、寬，請學生閉上眼睛想象出這個圖形，并說說它的面積是多少，為什么。這時信息環(huán)境再次發(fā)生變化，學生的原有認知結(jié)構(gòu)無法同化新環(huán)境提供的信息，這就進入了認知結(jié)構(gòu)進行重組與改造的“順應(yīng)”過程。當學生通過想象就能口答出長方形的面積時，面積計算的算理、算法完全得到了“內(nèi)化”。這個從“全鋪”到“巧鋪”“意鋪”再到“想象”的過程，學生從實際操作逐步過渡到用思維去把握對象，不斷地“同化”“順應(yīng)”，從而達到新知的“內(nèi)化”，正是數(shù)學思維的內(nèi)涵呈現(xiàn)。

三、策略“化歸”是數(shù)學思維的本質(zhì)要求

解決問題的策略“化歸”，往往不是直擊問題，而是換道、變形、轉(zhuǎn)化，化難為易、化繁為簡、化生為熟……例如，像23×38這樣兩位數(shù)乘兩位數(shù)的豎式計算教學，“能口算嗎？選擇合適的方式把你口算的過程記錄下來。”學生利用老師提供的點子圖、表格等將23×38轉(zhuǎn)化為如下的幾道算式：20×30、20×8、3×30、3×8。“我把23×38變成了整十數(shù)乘整十數(shù)、一位數(shù)乘整十數(shù)、一位數(shù)乘一位數(shù)的計算，這樣我就會做了。”“那能不能把你的這個計算過程用豎式表示出來？”學生列出了這樣的豎式：

“回憶一下23×8、23×30的豎式計算，再把這兩個豎式和23×38的豎式計算進行比較，想一想你還可以怎樣讓豎式簡便？”“原來把23×8、23×30這兩個豎式合在一起就行了。”“有了數(shù)位知識，用十位上的數(shù)去乘另一個乘數(shù)，積寫在十位的下面就行了，個位的0都可以省略呢！”……這些方法都是“化歸”法的巧妙運用，以此類推，后面的多位數(shù)乘多位數(shù)的筆算都可以化歸成原先已經(jīng)得到了解決并較為簡單的“一位數(shù)乘一位數(shù)”的問題。通過這樣的教學，長期堅持，潛移默化，學生的觀察、猜想、分析、歸納、概括及邏輯論證等數(shù)學思維都會“柳暗花明又一村”。

（責任編輯：奚春皓）