關(guān)于高中數(shù)學(xué)離心率題型解法的有效解決技巧

楊新波

【摘要】在高中數(shù)學(xué)中，離心率是一個(gè)比較抽象的概念，它是描述圓錐曲線性質(zhì)的一個(gè)的概念，同時(shí)它也是圓錐曲線的一個(gè)非常重要的屬性。離心率的定義是：到定點(diǎn)的距離與到直線的距離的比是常數(shù)（記作）的點(diǎn)的軌跡叫做圓錐曲線，其中常數(shù)就是圓錐曲線的離心率，它可以描述橢圓的扁圓程度、雙曲線的開(kāi)口大小，所以這類知識(shí)相關(guān)的題型所考察的重點(diǎn)是離心率的數(shù)值。但是由于離心率的概念比較抽象，給學(xué)生的學(xué)習(xí)增加了一定的困難。本文就關(guān)于高中數(shù)學(xué)離心率題型解法的有效解決技巧進(jìn)行研究。

【關(guān)鍵詞】高中數(shù)學(xué);離心率;題型解法

引言

數(shù)學(xué)解題思想的關(guān)鍵之處在于把學(xué)生所學(xué)的知識(shí)融合在一起，有利于鞏固學(xué)生所學(xué)的數(shù)學(xué)知識(shí)點(diǎn)，這幫助學(xué)生建立一個(gè)良好的認(rèn)知結(jié)構(gòu)，發(fā)展學(xué)生的邏輯推理能力，提高高中數(shù)學(xué)的教學(xué)質(zhì)量和教學(xué)水平。每一類數(shù)學(xué)題型都有相應(yīng)的解題技巧，只要學(xué)生掌握了該類題型的解題技巧，就能夠達(dá)到舉一反三的教學(xué)效果。

一、高中數(shù)學(xué)離心率題型的概念

在高中數(shù)學(xué)教材里，離心率是一個(gè)比較重要的幾何概念，因此離心率與幾何圖形有著非常緊密的聯(lián)系，圓錐曲線的離心率題型是高考中重點(diǎn)題型，一般都以壓軸題的形式出現(xiàn)，而且離心率題型考核的形式多種多樣，考試題型將斜率、平行、離心率以及向量結(jié)合在一起，甚至與物理知識(shí)相結(jié)合。高中數(shù)學(xué)的離心率題型主要考察學(xué)生的數(shù)學(xué)綜合能力，因此高中數(shù)學(xué)教師在教學(xué)的過(guò)程中，教師要引導(dǎo)學(xué)生對(duì)離心率題干中信息進(jìn)行分析，尋找出已知信息，找到解題思路，進(jìn)而達(dá)到解題的目的。

二、高中數(shù)學(xué)離心率題型的解題技巧

在筆者的教學(xué)過(guò)程中對(duì)學(xué)生進(jìn)行離心率知識(shí)點(diǎn)教導(dǎo)時(shí)，引導(dǎo)學(xué)生培養(yǎng)從簡(jiǎn)單的變數(shù)中觀察隱含的數(shù)學(xué)規(guī)律，培養(yǎng)學(xué)生善于用數(shù)字、圖形相結(jié)合的思想解答高中數(shù)學(xué)的幾何題。初次之外，高中數(shù)學(xué)離心率對(duì)高中生的數(shù)學(xué)計(jì)算能力、設(shè)想能力有充分的考驗(yàn)，部分學(xué)生因?yàn)閷?duì)高中數(shù)學(xué)的離心率比較畏懼，所以在考場(chǎng)上一旦有離心率的題型就選擇“不答”的情況，針對(duì)這種情況，高中數(shù)學(xué)老師一定要注重突破學(xué)生的畏懼心理，在教學(xué)中結(jié)合經(jīng)典例題幫助學(xué)生找到高中離心率題型的突破口

1、認(rèn)真審題，捕捉“題眼”

審題是高中數(shù)學(xué)離心率題型解答的首要步驟，有助于學(xué)生從離心率的知識(shí)點(diǎn)正確的解答思路進(jìn)行切入，挖掘隱藏條件，避免解體出現(xiàn)失誤。所以在日常練習(xí)過(guò)程中應(yīng)該注重審題，避免出現(xiàn)因題目的相似性而匆匆答題導(dǎo)致失分。以

例題1：考察雙曲線的標(biāo)準(zhǔn)方程及公式的題目為例：若雙曲線的離心率是2，則實(shí)數(shù)的值是多少？

從這道例題來(lái)看根據(jù)雙曲線的標(biāo)準(zhǔn)方程式確定、，根據(jù)公式求出的值，得出.

2、明確考點(diǎn)，正確計(jì)算

高中數(shù)學(xué)解答題能夠考查學(xué)生對(duì)知識(shí)點(diǎn)的把握和計(jì)算能力，是一種綜合性考查方式。所以高中數(shù)學(xué)解答題不僅要求學(xué)生會(huì)解答，更要注重答題的高效性，達(dá)到在有限的時(shí)間中憑借自身所掌握的知識(shí)點(diǎn)取得更多的分。所以高中數(shù)學(xué)的離心率學(xué)習(xí)過(guò)程中注重培養(yǎng)學(xué)生的等價(jià)轉(zhuǎn)化思想、函數(shù)方程思想、分類討論思想。在答題過(guò)程中結(jié)合綜合思想把握考點(diǎn)，進(jìn)行正確的計(jì)算。

例題2：已知、是橢圓C：（a>b>0）的左、右兩個(gè)焦點(diǎn)，若橢圓C上存在一點(diǎn)M，使得，求橢圓離心率的取值范圍。

這道題需要學(xué)生根據(jù)橢圓的定義和條件建立方程，利用基本不等式建立、的不等式，從而求出橢圓離心率的取值范圍進(jìn)而進(jìn)行解答。

3、語(yǔ)言規(guī)范，書(shū)寫工整

高中數(shù)學(xué)離心率解答題是高中數(shù)學(xué)考試的必考重點(diǎn)之一，并且解答過(guò)程中要求學(xué)生數(shù)學(xué)較為繁瑣的解題過(guò)程。若在解答過(guò)程中出現(xiàn)語(yǔ)言不規(guī)范、字跡不整齊的情況則會(huì)導(dǎo)致閱卷老師閱讀不清，導(dǎo)致考試丟分。所以高中數(shù)學(xué)老師在日常教學(xué)過(guò)程中，教師應(yīng)該做好引導(dǎo)，保證學(xué)生在離心率解答題的解答過(guò)程中用語(yǔ)規(guī)范，字跡工整。

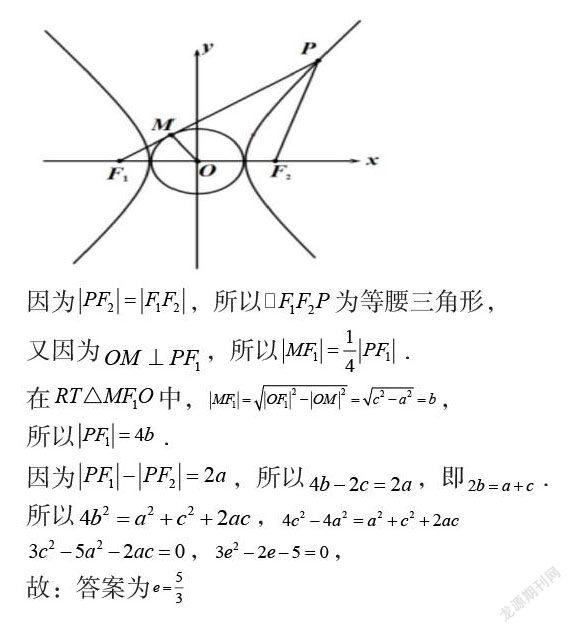
例題3：雙曲線的左右焦點(diǎn)為，是雙曲線上一點(diǎn)，滿足，直線與圓相切，求雙曲線的離心率.

本道例題主要考察學(xué)生的思維能力以及對(duì)幾何的解析能力，求解雙曲線的離心率或離心率的取值范圍，是高中數(shù)學(xué)離心率考察的重要題型，也是近年來(lái)高考的熱門題型之一，同時(shí)也是高考數(shù)學(xué)的重點(diǎn)內(nèi)容，解決該類問(wèn)題的關(guān)鍵之處在于把握曲線的本質(zhì)，根據(jù)已經(jīng)信息，理清曲線與圓的位置關(guān)系，進(jìn)而達(dá)到求解的目的。

結(jié)束語(yǔ)：綜上所述，離心率是近年來(lái)數(shù)學(xué)高考的重要題型也是常考題型，高中數(shù)學(xué)老師在開(kāi)展教學(xué)過(guò)程中從解題思路進(jìn)行教學(xué)之外注重從多個(gè)層面考查學(xué)生對(duì)圓錐曲線知識(shí)和分析問(wèn)題的綜合能力。離心率作為圓錐曲線中的重要元素之一，其變化會(huì)直接影響著圓錐曲線的形狀和類型，所以軌跡問(wèn)題與圓錐曲線的三要素密切相關(guān)。除此之外由于不同的圓錐曲線的離心率有著不同的范圍，所以在解答過(guò)程中求取參數(shù)的取值范圍是近年來(lái)的重點(diǎn)考題之一。除了以上答題技巧之外，高中數(shù)學(xué)老師對(duì)學(xué)生的答題規(guī)范和答題重點(diǎn)應(yīng)該做到時(shí)刻關(guān)注，避免學(xué)生出現(xiàn)失分的情況。

參考文獻(xiàn)：

[1]王曉云.高中數(shù)學(xué)求離心率e值的解法初探[J].教書(shū)育人，2017（20）：79-79.

[2]沈文慧.高中數(shù)學(xué)“離心率問(wèn)題”的求解方法[J].理科考試研究：高中版，2015，22（11）：6-6.

[3]孟凡勛.圓錐曲線離心率問(wèn)題的探究策略[J].高中數(shù)學(xué)教與學(xué)，2018（2）：123-124.