淺析小學(xué)數(shù)學(xué)課堂教學(xué)中“數(shù)形結(jié)合”教學(xué)方法的運用

王希武

摘 要：“數(shù)形結(jié)合”是數(shù)學(xué)轉(zhuǎn)化思想的重要表現(xiàn)，有助于教師更透徹地講解教學(xué)內(nèi)容，有助于學(xué)生對數(shù)學(xué)知識更好地理解和運用，無論是教師教學(xué)還是學(xué)生解題的過程中，它都發(fā)揮著重要的作用。淺析“數(shù)形結(jié)合”思想在小學(xué)數(shù)學(xué)課堂教學(xué)中的運用方法，培養(yǎng)學(xué)生在數(shù)學(xué)學(xué)習(xí)中善于運用“數(shù)形結(jié)合”的思維能力，以此來提高學(xué)生在學(xué)習(xí)與生活中對遇到的數(shù)學(xué)問題的解決能力。

關(guān)鍵詞：初中數(shù)學(xué);數(shù)形結(jié)合;運用方法

數(shù)量關(guān)系與空間形式，是數(shù)學(xué)研究的兩個主要內(nèi)容，如果將“數(shù)”與“形”分開研究，就會出現(xiàn)應(yīng)用范圍小、發(fā)展速度慢的情況。單純地去研究數(shù)學(xué)中的“數(shù)”，缺少直觀性的觀察與判斷，將很難對“數(shù)”有更深刻的理解;單純地去研究數(shù)學(xué)中的“形”，缺少細節(jié)性的數(shù)據(jù)對比，這也很難對“數(shù)”有更深入的研究。小學(xué)是學(xué)生數(shù)學(xué)學(xué)習(xí)的開始階段，應(yīng)該把“數(shù)”與“形”結(jié)合起來，作為一種數(shù)學(xué)思想來教學(xué)。充分發(fā)揮“數(shù)形結(jié)合”思想的作用，以此加強初中生對數(shù)學(xué)知識的理解與掌握，培養(yǎng)學(xué)生善于運用“數(shù)形結(jié)合”思維的能力。但如何把“數(shù)形結(jié)合”思想有效地應(yīng)用在初中數(shù)學(xué)課堂教學(xué)中，讓學(xué)生更好地去理解和運用呢？這成為所有數(shù)學(xué)教育工作者不得不思考的問題。

一、化抽象為具體，有助于學(xué)生對數(shù)學(xué)概念的理解

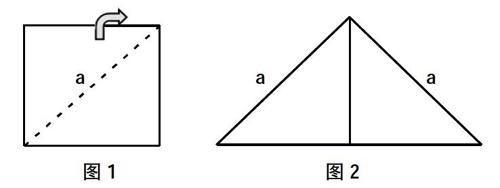
數(shù)學(xué)普遍是抽象的知識結(jié)構(gòu)，而這些抽象的知識中，概念、公式更是千百年來眾多數(shù)學(xué)家的智慧濃縮，小學(xué)生的數(shù)學(xué)知識有限，對一些概念、公式的證明過程與思維過程難以理解。教師用“數(shù)形結(jié)合”的思想表示這些公式定理，就會讓學(xué)生更好地去理解和記憶。例如，正方形面積公式：S=邊長×邊長，這是學(xué)生以前學(xué)過的內(nèi)容，在“認識多邊形”一課中，需要把多邊形拆分成學(xué)生知道的圖形進行多邊形面積計算，但在一些例題中，多邊形拆分后只能得到正方形對角線的長度，讓學(xué)生求正方形的面積，這樣學(xué)生就要利用正方形的第二面積公式：S=對角線×對角線÷2，如何讓學(xué)生快速理解并熟練運用這個公式，教師在教學(xué)時就要用到數(shù)形結(jié)合的思想，把正方形轉(zhuǎn)化成三角形。

如圖1，把正方形按照對角線剪開，把上半部分順時針翻轉(zhuǎn)270°，得到圖2，一個等腰直角三角形，此三角形的面積就等于正方形的面積，即S=a×a÷2，也可以得到正方形的第二面積公式：S=對角線×對角線÷2。教師借助圖形的變化，把正方形轉(zhuǎn)變成小學(xué)生可以熟練運用的三角形面積公式，把抽象的數(shù)學(xué)概念圖形化，讓學(xué)生可以更直觀地理解，有助于學(xué)生對數(shù)學(xué)概念的掌握和運用，這樣學(xué)生可以更快速地去計算多邊形的面積，達到教學(xué)目的。

二、化繁瑣為簡單，有助于學(xué)生對數(shù)學(xué)情感的建立

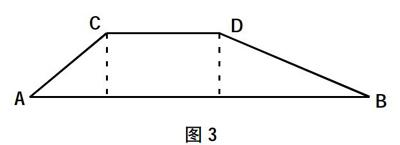
小學(xué)數(shù)學(xué)應(yīng)用題中有非常繁瑣的數(shù)量關(guān)系式，一些思維邏輯能力差的學(xué)生，很容易把這些關(guān)系搞混，造成解題的錯誤，長此以往，學(xué)生對數(shù)學(xué)逐漸失去信心，產(chǎn)生消極的學(xué)習(xí)態(tài)度。因此，教師在小學(xué)數(shù)學(xué)教學(xué)過程中，要讓學(xué)生學(xué)會運用“數(shù)形結(jié)合”的思想去解題，讓繁瑣的數(shù)學(xué)變得簡單，用圖形培養(yǎng)學(xué)生良好的數(shù)學(xué)情感，增強學(xué)生數(shù)學(xué)學(xué)習(xí)的興趣。如題：一輛小卡車從A地向B地送貨，已知A地到B地是一個陡峭的地形，上坡的速度是20 km/h，平地的速度是30 km/h，下坡的速度是40 km/h，去的時候，平地用了2個小時，下坡用了4個小時，總共用了7個小時，求小卡車送完貨返回時要用多少時間。學(xué)生運用“數(shù)形結(jié)合”的思想畫圖解題，如圖3。

學(xué)生通過畫圖，可以分析出從B地返回A地時，下坡變成了上坡，上坡變成了下坡，因此，得到結(jié)論：與從A到B相比，B到A時，上下坡的路程都發(fā)生了變化，平地的路程沒有發(fā)生變化。通過畫圖，把復(fù)雜的關(guān)系直觀地呈現(xiàn)在學(xué)生面前，讓學(xué)生對題中的邏輯關(guān)系更為清楚，降低了此題的難度，學(xué)生在解題中也會獲得算出正確結(jié)果后的滿足感，增加了學(xué)生數(shù)學(xué)學(xué)習(xí)的趣味性，有助于學(xué)生數(shù)學(xué)情感的建立。

小學(xué)數(shù)學(xué)教學(xué)中滲透“數(shù)形結(jié)合”思想，既符合小學(xué)生數(shù)學(xué)的認知規(guī)律，有助于學(xué)生對數(shù)學(xué)概念的理解和掌握，又極大地增加了數(shù)學(xué)解題時的趣味性，有助于小學(xué)生數(shù)學(xué)情感的培養(yǎng)和建立。因此，教師在小學(xué)數(shù)學(xué)教學(xué)的過程中，要十分重視和培養(yǎng)學(xué)生對“數(shù)形結(jié)合”思想的運用和思維習(xí)慣，讓學(xué)生更好地去理解和運用，以此來提高學(xué)生在學(xué)習(xí)與生活中對遇到的數(shù)學(xué)問題的解決能力。

參考文獻：

[1]李文玲.“數(shù)形結(jié)合”思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用分析[J].西部素質(zhì)教育，2016（1）：173.

[2]蔣菲.小學(xué)數(shù)學(xué)教學(xué)中數(shù)形結(jié)合有效性的思考[J].小學(xué)科學(xué)，2016.

編輯 謝尾合