“三先三后”教法在小學數學教學的應用

【摘要】本文論述“三先三后”教法在小學數學教學中的應用策略，認為數學教學應該讓學生掌握正確高效的學習方法，提出先理解后記憶、先思考后解題、先訂正后拓展等教學建議，讓學生從“學會”走向“會學”、從“會學”走向“樂學”。

【關鍵詞】小學數學 三先三后教學法 轉化 推理

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2021）05-0099-03

數學學習要講究方法，只有方法正確才能取得理想的學習效果。學生如果能在學習知識的同時，掌握正確高效的學習方法，就可以讓自己走進一個精彩的數學世界，使自己從“學會”走向“會學”、從“會學”走向“樂學”。本文介紹先理解后記憶、先思考后解題、先訂正后拓展等三種教學方法，以期拋磚引玉，更好地指導學生學好數學。

一、先理解后記憶

部分學生在學習數學時常采用認真聽、使勁練的方法，一開始可能效果還不錯，但時間一久我們就會發現，學生學習數學變得很辛苦，成績不升反降。其實數學學習不應該過于強調記憶，而應該注重理解。數學的概念、規則、方法都要在理解的基礎上進行識記和運用，學生的學習才會變得輕松愉快，記憶才會更加牢固，學習才會更加高效。那么，怎樣幫助學生更好地理解數學知識呢？

（一）“表達說理”激發理性思維

只有理性思維真正參與，才會讓學生從感知層面走向理解層面。“表達說理”無疑是一個激發理性思維的好方法。“表達說理”有很多途徑，例如口頭的言語表達，還有動作表達、圖像表達、算式表達，等等。在教學時，教師要讓學生積極主動地表達出自己的思考和理解，充分調用已有的認知經驗進行表達與交流，進而在不斷地辨析中掌握真理，理解數學知識本質。

其中，我們最常用的是口語表達，即鼓勵學生用自己的話說出數學道理。讓學生把“理”說出來，通過表達說理深入走進理性思維，課堂也會因此展現數學知識的生成過程，揭示數學結論背后的“為什么”，學生會因此透過感覺走進理性的世界。例如在教學“長方形的面積計算”時，我們都知道長方形的面積=長×寬，但是大部分學生只是死記硬背這個公式，并不理解這個公式背后的道理。長是長度、寬也是長度，長度和長度按理只能相加或相減，怎么會乘起來呢？這樣乘起來為什么就是面積呢？通過說理，學生能夠深刻理解公式背后的本質屬性，進而牢固掌握公式的原理和知識的來龍去脈。如果不講理，數學知識就會變得枯燥難懂，這時要識記并靈活運用就很難了。

（二）“數形結合”走向深度理解

數學因為比較嚴謹抽象，所以要學好并不是一件輕而易舉的事。這時如果教師能借助直觀的圖形來幫助分析和思考，可以讓學生深入學習、理解數學知識的本質。因為人類的大腦對形象、生動的圖形有天生的喜愛，圖形會讓我們更容易接受和思考。在日常教學中，常用的圖有方格圖、線段圖、樹形圖等。

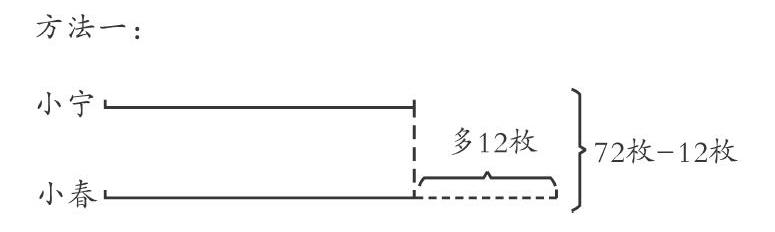
例如，“小寧和小春共有72枚郵票，小春比小寧多12枚郵票。兩人各有多少枚？”學生在解答本題時，由于找不到解題的突破口，導致無從下手。此時，如果先畫圖，把題目的條件和問題在圖形上表示出來，再借圖思考，學生就能想到很多解題的方法。

總數72減去小春比小寧多的12枚，兩人現在的郵票就同樣多了。再除以2就算出小寧有30枚，小春有30加12等于42枚。

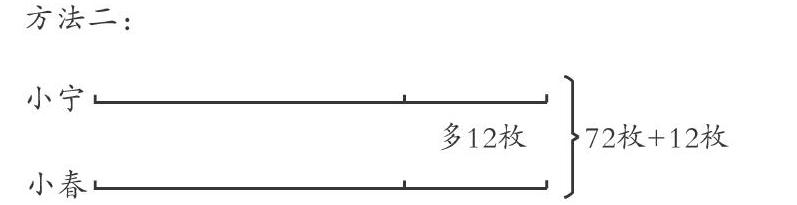
總數72加上12兩人的郵票就變得同樣多，再除以2就算出小春有42枚，42減去12就算出小寧有30枚。

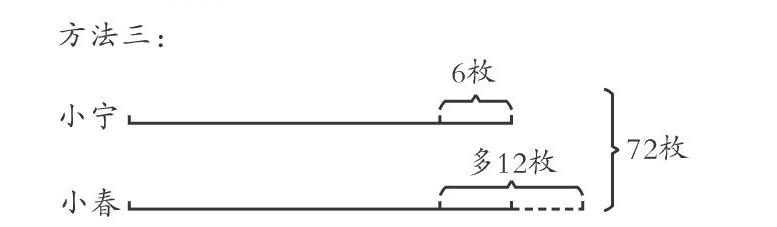
郵票總數不變，把小春比小寧多的12枚分一半給小寧，兩人的郵票就變得同樣多。用72除以2得36，小寧有36減6得30枚，小春有36加6得42枚。

可見，直觀的圖形有助于我們把抽象的問題直觀化、解決問題的策略多樣化。另外，利用圖形解決“數”的問題，還有助于我們建立數學模型、方便理解和運用。如在教學《乘法分配律》時，學生常常會把乘法分配律和乘法結合律弄混，如果能運用圖形來理解，則可以輕松得出答案，（6+4）×5=6×5+4×5，即大長方形=黑色長方形+白色長方形。

這樣，當我們把乘法分配律和圖形建立聯系來理解，在運用時就不會混淆。

二、先思考后解題

學習數學很容易被人錯誤地認為做好了題目就是學好了數學，其實學好數學不一定要做很多題，也不是用“刷題”來代替思考。學習數學，關鍵還是要學會思考。先會思考，再來解題，水到渠成。因此，教師要重視引導學生學會數學思考。數學思考的方法很多，這里介紹轉化和推理兩種。

（一）轉化——數學思維的綠色通道

轉化，不但可以使問題化繁為簡、化難為易，而且能提高學生的思維品質。轉化的類型多種多樣，可以把新知轉化為舊知、把復雜的問題轉化為簡單的小問題、把一般的問題轉化為特殊的問題等。無論是數的運算，還是圖形的面積計算或者數學問題解決等，都會用到轉化。可以說，轉化是數學思維的一條綠色通道。

例如，甲、乙兩車分別從A、B兩地同時相對開出，經過2小時相遇，相遇后各自繼續前進，又經1.5小時，甲車到達B地，這時乙車距A地還有35千米，求A、B兩地的距離。這道行程問題，因兩車同時出發到相遇各用2小時，從相遇到甲車到達B地各用1.5小時，在每個階段所用時間相同，因此我們可抓住時間這個不變量進行轉化，把此題轉化為：兩車同時從兩地相向而行，2小時合行了一個全程，1.5小時合行的路程比全程少35千米，由此推出兩車0.5小時合行35千米，則兩車1小時合行35÷0.5=70千米，此時很容易求出A、B兩地相距70×2=140千米。

詳解為：2-1.5=0.5（小時），35÷0.5=70（千米），70×2=140（千米）。

答：A、B兩地的距離為140千米。

該題還可以這樣轉化：把甲、乙兩車看成同向而行，行了3.5小時，甲乙相差35千米，可以求出速度差，35÷3.5=10千米/時。同時可知，乙行2小時的路程甲只需1.5小時，也就是1.5小時的路程差乙要花另外的0.5小時來完成，這樣可以求出乙的速度：10×1.5÷（2-1.5）=15÷0.5=30千米/時。因此總路程是：30×3.5+35或（30+10）×3.5=140千米。

詳解為：35÷3.3=10（千米/時）

10×1.5÷（2-1.5）

=15÷0.5

=30（千米/時）

30×3.5+35=140（千米）或（30+10）×3.5=140（千米）

答：A、B兩地的距離為140千米。

另外，我們還可以將該題轉化為比的知識來解決。由題意知甲車1.5小時行的路程=乙車2小時行的路程，抓住路程相等做轉化得出：甲、乙兩車速度比=甲乙兩車時間比的反比=2∶1.5=4∶3;又因為從出發到相遇再到離開，甲、乙兩車各行了3.5小時，此時抓住時間相等做轉化得出：甲、乙兩車各行3.5小時的路程比=甲、乙兩車的速度比=4∶3，由此推出甲3.5小時比乙3.5小時多行了4-3=1份，而1份恰好是35千米，全程有這樣的4份，所以全程為35×4=140千米。

詳解為：2∶1.5=4∶3

35÷（4-3）=35（千米）

35×4=140（千米）

答：A、B兩地的距離為140千米。

總之，轉化法在數學學習中有著廣泛的應用。如果運用巧妙，一定能旗開得勝，達到事半功倍的效果。因此，教師在平時的數學教學中一定要加強轉化的教學和指導。

（二）推理——數學思維的重要基石

學習數學重在培養學生的邏輯推理能力，這是數學素養的核心。什么是推理呢？推理是指從一些事實出發，依據規則推出其他結論的思維過程。主要包括兩類：一類是從特殊到一般的推理，推理形式主要有歸納、類比;另一類是從一般到特殊的推理，推理形式主要有演繹。無論是哪種推理，都強調其中的邏輯關系。因此，引導學生多開展觀察、比較、猜想、實驗、類比、歸納等很有必要，可以促進學生在推理中體會思考和發展的樂趣。

例如，●○●○○●○○○●（）●○○○○○，一共有多少個球？

①觀察顏色，發現顏色出現的循環，進行顏色不同的推理。②觀察個數，發現個數出現的循環，進行個數不同的推理。③將直觀圖形轉化為數字符號的推理。1×5+（1+2+3+4+5）=20。

又如，把前一百個單數（奇數）相加，和是多少？

1+3=4

1+3+5=9

1+3+5+7=16

1+3+5+7+9=25

……

此時，教師可以引導學生觀察思考，得數4、9、16、25分別是2×2、3×3、4×4、5×5，那么此題的答案是不是等于100×100？

數學的本質隱藏在數學知識的內部，很多數學知識都可以用邏輯推理來幫助理解。從邏輯推理的視角開展數學教學不僅可以讓數學變得生動有趣，還可以讓學生感覺到通俗易懂。所以說，推理是指引我們深入思考的“燈塔”，更是用學到的有限知識去迎接未來無限挑戰的利器。

三、先訂正后拓展

在學習數學知識的過程中出錯是難免的，但千萬不要把錯題當作魔鬼，排斥或掩蓋它。很多學生也排斥糾錯。事實上，訂正錯題是數學學習的重要一環，因為錯題能反映學生對新知識的掌握情況，也可以反映學生的理解水平，正視錯誤不僅可以扎實基礎，還可以為進一步拓展提升提供參照。那么，教師該怎樣指導學生訂正數學錯題？如果學生只是為了完成任務而草草了事、流于形式，那是低效的;或者訂正時只是過分關注結果，不深入分析錯因，不注重思維過程，也很難提高學生的水平。所以，教師要引導學生不要只關注一時的糾錯，還應重視后期對錯誤資源的再度利用。

筆者認為，“三環訂正法”可以引導學生養成良好的訂正習慣，幫助學生掌握科學的訂正方法。“三環訂正法”是依據心理學和學科內容科學設計的，包含“診斷錯因，厘清知識”“規范整理，篩選分類”和“定期復習，鞏固遷移”三個環節，分別在當天、周末和月末三個時機應用。

（一）診斷錯因，厘清知識

1.錯題務必當天訂正，訂正之前應仔細閱讀題目，深入思考，找出錯誤所在及原因;如果自己找不出錯因，可以尋求同學或老師的幫助，借助他人力量找出錯因。

2.將錯題抄在便利貼上，注明錯題的來源、頁碼及題號，再寫出錯因，但不能用“我不會”“太粗心了”等寬泛的表述，而應找出與課本對應的具體知識點。

3.在便利貼上自主寫出訂正過程，步驟應盡量翔實。

4.將寫好錯因和正解的便利貼貼在錯題的旁邊，以備老師二次批改。

（二）規范整理，篩選分類

1.每個周末，先把累積在作業本或試卷上的錯題重做一遍，再根據對錯題情況分成“掌握”和“易錯”兩個類別。

2.然后把貼在錯題旁邊的便利貼撕下來，分成兩類（“掌握”和“易錯”）粘貼到錯題本上。

3.“掌握”型的錯題不用再次訂正，“易錯”型的錯題要在錯題本上重新訂正一次，以備老師再次檢查和以后復習利用。

（三）定期復習，鞏固遷移

1.以每月為期，定時復習一次錯題本上的錯題;主要以查漏補缺為主，再開展尋找相似題型進行編題、練習。

2.梳理單元內所學知識，將錯題對應的知識點進行再溫習，形成結構圖。

3.學習小組的四位組員互換錯題本，檢查同學的糾錯情況，總結錯誤類型及原因，并在小組內交流、提醒。

4.總結全組成員的錯誤類型，整合成一份練習卷，各自回答，批改反思。

總之，數學學習需要方法，只有關注學習方法才能實現高效而有味的數學學習。因此，教師不僅要教學生數學知識，更要指導學生學習方法，讓每一名學生因為學習得法而享受數學世界的精彩和有趣。

作者簡介：葛敏輝（1982— ），浙江東陽人，大學本科學歷，高級教師，主要從事小學數學教學與研究。

（責編 林 劍）