由獨立重復實驗淺談高中數學建模
馬曉娟

摘 要:獨立重復實驗是研究隨機現象的重要途徑之一,很多概率模型的建立都以獨立重復實驗為背景。數學模型是數學與實際現象之間的橋梁,數學核心素養包括數學建模、數據分析等素養。本文以“獨立重復實驗與二項分布”教學為例,探討了如何開展高中數學建模活動。
關鍵詞:高中數學;數學建模;獨立重復實驗
中圖分類號:G427? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A? ? ? ? ? ? ? ? ? ? 文章編號:2095-624X(2021)30-0059-02
引 言
近年來,數學模型和數學建模這兩個術語使用的頻率越來越高,人們對數學建模的關注程度也與日俱增。數學的應用不僅在它的傳統領域——物理領域繼續取得重要進展,還迅速進入人們生產和生活的許多新領域,如經濟、人口、生態、醫學、社會等領域。人們樂于在外出時乘坐舒適、快捷又安全的大型客機,其整個設計過程是由一種將數學與計算機相結合的被稱為計算機輔助設計(CAD)的先進的數學技術完成的。其生產過程則是用工程師建立的控制生產過程的數學模型,對控制裝置做出相應的設計和計算后實現的。為了保障人民的生命健康,醫學專家經常開發和研制新的藥物和醫療器械,而一種新藥或器械的試制必須經過反復實驗,以獲得充足的數據,并利用數學方法模擬療效數學模型后方可分析療效,從而有效地指導臨床治療[1]。
高中數學新教材和舊教材相比,更注重數學的應用和對數學核心素養的培養,注重應用數學知識構建模型,從而培養學生的數學建模能力。
一、內容分析
獨立重復實驗與二項分布是用事件的獨立性來研究一類問題,概率論中被稱為伯努利概型,伯努利概型是概率論中研究較多的數學模型之一,概括了許多實際問題,因而很有實用價值。它也為今后進一步學習概率論奠定了基礎。值得一提的是,我們由伯努利概型可以解決一類“隨機游動”的問題。下面,筆者將結合教材中的例題,以及醉漢隨機游走和姚明投球命中率的實例,按照數學建模的五個步驟,建立二項分布模型,發展學生的數學建模和數據分析素養。這也是這節課的重點,即理解獨立重復試驗、二項分布,并應用二項分布模型解決一些簡單的實際問題。學生可采用自主探究、合作交流的形式,從具體事例中歸納出數學概念,充分體會知識的發現過程,進而發展自身的數學抽象素養;利用二項分布的有關知識解釋生活中的現象,用數學的語言表達世界,發展數學建模和數據分析的核心素養[2]。
二、學生情況分析
學生已有的認知基礎:通過前面的學習,學生已經初步掌握了有關概率和統計的基礎知識,如可能事件概率、互斥事件概率、條件概率、相互獨立事件概率的求法、隨機變量分布及簡單的組合知識。另外,學生也學習過一些研究問題的方法,如特殊到一般、具體到抽象等,且有了一定的抽象概括能力。這為學生學習本節內容做好了知識和方法上的鋪墊。
可能遇到的困難:本節內容是從生活實例出發,引導學生歸納出抽象n重伯努利實驗的概型,并利用伯努利概型的有關知識解釋生活中的一些現象。這對學生抽象概括能力和應用數學語言的表達能力要求較高。利用一個新的概率模型解釋生活中的現象對學生來說有一定的困難。教學難點:利用二項分布模型來解決實際問題,即伯努利模型的構建。
三、教學過程設計
(一)分析實例
實例1:隨機游走模型
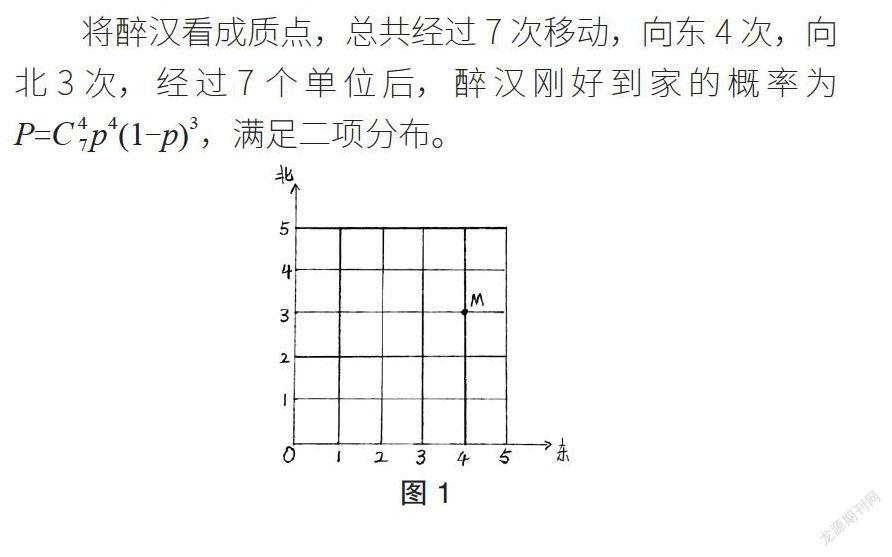
想象在曼哈頓東西南北格點化的街道中有一個醉漢,他每次到達一個交叉路口時都會隨機選擇向東、向北兩個方向中的一個,然后繼續前行;在走到下一個路口時又隨機選擇一個方向……如此繼續下去,這個醉漢回到家的概率是多少?
模型假設:醉漢每個時間單位到達一個交叉路口,向東或者向北前進,向東的概率為p,向北的概率為1-p,假設醉漢的家在點M(4,3)處(見圖1),求經過7個時間單位后醉漢剛好到家的概率。
模型建立與求解:
將醉漢看成質點,總共經過7次移動,向東4次,向北3次,經過7個單位后,醉漢剛好到家的概率為P=C47p4(1-p)3,滿足二項分布。
實例2:姚明投球
姚明作為中鋒,他職業生涯的罰球命中率為0.8,假設他每次投籃的命中率相同,請問他4投3中的概率是多少?(以上有關數據由學生課前查閱資料并收集整理)
模型假設:假設姚明每次投籃的命中率是相同的。
模型建立與求解:
問題:姚明作為中鋒,他職業生涯的罰球命中率為0.8,假設他每次投籃的命中率相同,請問他4投3中的概率是多少?設姚明投中球的個數為x,x的分布列是怎樣的?
學生活動:小組合作討論。
分解問題:(1)在4次投籃中他恰好命中3次的情況有幾種?(2)說出每種情況的概率是多少?(3)上述四種情況能否同時發生?(4)設姚明投中球的個數為x,x的分布列是怎樣的?
教師行為:引導學生觀察分析,讓學生大膽去說,教師逐步修正,完善學生的說法,培養學生分析問題和解決問題的能力。
答案(學生拿自己的草稿在投影下講):
Ai表示姚明第i次投中球,則表示姚明第i次沒投中球。姚明4投3中包含以下事件:,,
,共種,每種事件的概率為。故4投3中的概率為。x的分布列為(見表1)。
上述解答是一個對前面所學知識的應用過程。學生看到最后的結果,有一種“撥開云霧見青天”的感覺,這不就是二項式定理嗎?學生熱情高漲,把對知識的學習和掌握過程變成了對知識的探索、發現、總結、創新的過程。

