例談高中數學基于“最近發展區”的教學實踐策略
黃育明


[摘? 要] 在高中數學教學過程中,教師需深入研究學生的現有發展水平,認清潛在的發展水平,以新的目標為指引,制定適宜的發展要求,努力在數學課堂中創設學生的最近發展區,促進學生在最近發展區內發展,實現教學效果最優化,促使學生發展最大化.具體來說,教學中要以舊引新,關聯生活,類比引入,巧妙設疑,促進學生在最近發展區內逐步發展.
[關鍵詞] 最近發展區;高中數學;數學素養
20世紀70年代,維果茨基在教學與發展的問題中提出了最近發展區理論,他認為教學需從學生的最近發展水平入手,并著眼于其最近發展區,才能有效超越最近發展區,進入更高的發展區. 因此,教師作為學生學習的引導者,需深入研究學生的現有發展水平,并認清潛在的發展水平,以新的目標為指引,制定適宜的發展要求,努力在數學課堂中創設學生的最近發展區,促進學生在最近發展區內發展,實現教學效果最優化,促使學生發展最大化. 筆者認為最近發展區在高中數學教學中的應用可從如下方面著手.
[?]以舊引新,建立新舊知識之間的最近發展區
數學知識間的緊密聯系,舊知的掌握和運用水平影響著學生對新知的理解和認識. 因此,我們可以舊知為抓手,找準新舊知識之間的連接點,有目的地設計一些富有思考力的問題,搭建好新舊知識的橋梁,使其成為新知學習的可利用認知條件. 這樣一來,則可使學生努力開發自身的最近發展區,站在舊知的“草坪”上,試著跳一跳“摘”新知.
案例1:空間向量分解定理.
問題:已知平行六面體ABCD-A′B′C′D′中,有=e,=e,=e,請試著用e,e,e表示,,,.
設計意圖:復習舊知,從熟悉的向量加法的運算法則、平行向量的基本定理和共面向量定理等知識背景入手,綜合設計數學問題,逐步推理得出定理,并在對學生完成教學目標需要達到的最近發展水平進行檢測的同時,滲透從特殊到一般的思想,推動其理性思維能力的發展.
[?]關聯生活,建立理論與實際間的最近發展區
數學本身是與生活聯系最緊密的學科,數學教學的終極目標在于指引學生在生活實踐中運用數學知識去解決日常生活中的實際問題,這需要我們在教學中指引學生“我們的身邊隨時隨刻都存在著數學知識”,以此激勵學生探尋數學奧秘. 因此,要培養學生的數學興趣,激起數學探究動力,關聯生活是最好的途徑.新課標和新教材大力倡導聯系生活,讓數學生活化,教師則需因勢利導利用好貼近學生生活實際的情境,去吸引學生的創新欲望,使其快速建立起理論與實際的最近發展區,為學生的啟思導航提供智力平臺,將學生的思維調動到學習目的上來.
案例2:基本不等式.
問題:某商場限時舉行換季促銷,并設計了兩種降價的方案:方案①,一種商品在a折的基礎上再b折銷售;方案②,一種商品在折的基礎上再折銷售.請問以上兩種方案中,哪一種方案更省錢?
設計意圖:以上問題中呈現的“商品打折”現象是現實生活中的生動題材,讓新課的教學顯得更具有生命活力.教師緊緊扣住學生的好奇心和興趣一步步地進行引導,學生從自身的知識經驗和生活經驗出發親身體驗,抽象提煉,使得知識、技能和態度都得以發展,實現了最近發展區內的持續發展,同時也使學生不知不覺地領悟到數學的獨有韻味,讓數學素養自然得以鍛煉[1].
[?]類比引入,建立同類知識之間的最近發展區
高中生已經具有了一定的理性分析能力,概括能力相對于初中生也有了明顯的提升,思維也由著經驗性邏輯思維逐步向著抽象思維發展. 因此,在課堂引入中,教師可以類比引入的方式,從學生的最近發展區出發,從學生熟悉的場景入手,借助多種多樣的教學策略,嘗試設計新穎有趣的探索活動,建立同類知識之間的最近發展區,讓學生體會知識間的聯系,引導學生積極分析、主動質疑和巧妙生成.
案例3:數列.
探究1:結合以下六組數列,觀察數列變化的規律,說說有何共同點,又有何不同點.
(1)自然界中的植物花瓣的數目大多符合斐波那契數列的項:1,1,2,3,5,8,13,21,33,….
(2)哈雷彗星回歸地球的年份:1682,1758,1834,1910,1986,2062.
(3)從1988年至2012年中國在奧運會獲得金牌的數量:5,16,16,28,32,51,38.
(4)拉面經過對折后的根數變化:2,4,8,16,32,64,128,256,….
(5)儀式上的酒塔從最上層到最下層的酒杯數量:1,3,5,7,9.
(6)古詩詞中所包含的古塔上燈的數量:3,6,12,48,96,192.
探究2:(1)觀察表1中的兩組數列,請試著用n來表示第n項a,并歸納其中的關系式.
(2)倘若將n視為自變量,a視為函數值,a=f(n),數列中的每一項a和n是否都符合以上關系式?
(3)結合函數知識,試著寫出一個a=f(n)的表達式,并寫出它的前5項.
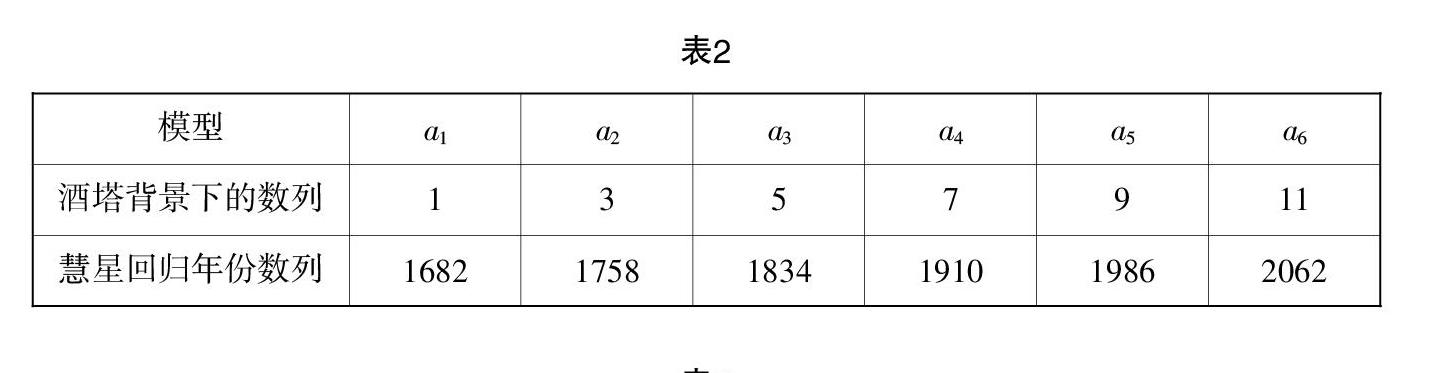
探究3:(1)觀察表2的兩組數列,試著歸納其相同點.
(2)從函數的角度,酒杯數a是關于n的什么函數?
(3)倘若某新人的婚禮需要一個10層的酒塔,那么需要的杯子數量是多少?說一說你是如何求的.
探究4:(1)觀察表3的兩組數列,請試著歸納其中的相同點.
(2)一根拉面,拉一下兩邊一合即為“一扣”.有人認為:“倘若每一扣長1米,則在制作過程中總長度比珠穆朗瑪峰還要長.”請試著結合該數列所對應的函數表達式闡述該觀點是否成立,并說明理由.
(3)若變古詩為“望去七層巍峨塔,紅燈向下成倍增,共有三百八十一,試問每層幾盞燈?”可否求出該數列?并說一說你的求法.
設計意圖:以上案例中,教師以導游的身份為學生打造了一個趣味性的探究環境,通過對生活中實例的一再探究,并呈現豐富多樣的課堂結構形態,讓學生對本章節的主要內容有充分的了解.同時,這樣一組層層深入的探究活動,引領學生進行已實現的最近發展區和新形成的最近發展區跨越. 整個過程中,學生親歷探究過程,充分發揮自身的主體地位,對問題進行遞進探究,層層深入地了解知識結構.教師高屋建瓴地實施調控,為學生的自主學習提供有效幫助,既與學生的認知過程相吻合,又體現了知識在探究中的自然生成,充分彰顯了新課改的理念[2].
[?]巧妙設疑,建立質疑與釋疑的最近發展區
教學設計中,教師需從學情和教材兩個方面著手分析,找準最近發展區,科學地制定目標,通過巧妙設疑去建立質疑與釋疑的最近發展區,讓學生的學習情緒漸入佳境,并促使學生深潛于最近發展區,自然而然地沉浸于質疑問難中進行分析、思考和體驗,實現最近發展區內的發展.
案例4:構成空間幾何體的基本元素.
問題1:試著利用6根相同程度的小棒去搭正三角形,最多你能搭幾個?
問題2:請思考:是否存在3條直線兩兩相互垂直?若存在,試舉例;若不存在,請說明理由.
設計意圖:課堂伊始教師就要貫徹好問題探究的建設性,學生從問題出發,將探究問題的視野從平面延伸至空間領域,這樣就可以從問題情境的創設較好地調動學生對立體幾何學習的熱情和欲望.事實也充分表明,學生的探究興趣盎然,思考與操作并行,學生在“做”的過程中積淀經驗,在“思”的過程中培育素養[3].
綜上所述,高中數學已經具有一定的深度和難度,教師的教學目標不僅僅要著眼于學生知識的掌握程度,更要關注到學生數學能力培養.教師需關注最近發展區理論的意義,并將其水到渠成地應用到日常教學中去,促進學生的發展.
參考文獻:
[1]? 王應密,呂莉. 基于“最近發展區”理論的教學設計探析——從“最近發展區”理論談教師在教學設計中應注意的幾個問題[J]. 內蒙古師范大學學報(教育科學版),2004(05).
[2]? 宋磊. 追根溯源,涵養素養——基于“最近發展區理論”的題根教學實踐與思考[J]. 中小學數學(高中版),2019(05).
[3]? 陳慧. 化繁為簡,貼近最近發展區的變式教學——導數與切線一課數學變式教學的設計與實踐感悟[J]. 數學學習與研究,2011(19).

