探討分析過程性評價中平時分的公平性

摘 要：過程性評價方法在教學過程中，每一位學生的情況都有所不同，表現不同，所以如何給每個學生打分，使其分數反映的是每個學生自己的真實學習狀態，減少渾水摸魚、濫竽充數的部分。即如何打分對每個學生更公平，是需要急需解決的一個問題。本文通過定性定量分析即層次分析法（Analytic Hierarchy Process）建立一個數學模型，可以得到較滿意的解決。

關鍵詞：過程性評價 公平 建模

1 引言

完善課程考核方式是提高課程教學效果的重要手段[1]。教師若在教學過程中采用傳統教學模式，評價形式單一，學生學習缺乏興趣，易產生畏難情緒，教學效果較差。過程性評價是針對終結性考核在教學評價中的過度使用造成了一系列的弊病而提出的一種教學評價方法[2]。其評價內涵豐富，具有多種多樣的定義，其中“師生過程性評價”研究團隊提出的定義被學界所認可，其定義為：“過程性評價是師生在教學過程中所進行的一種教學反饋，由反饋信息對教學過程進行調節，以改善學生的學習狀況而獲得預期的學習成果。”[3]

過程性評價自提出以來，在我國的各層次教學中的應用也日益廣泛，它有效減輕了學生面對終結性考核的壓力[4]，同時加強了學生平時的學習，避免出現考前臨時抱佛腳的情形。且更注重于考查學生解決問題的思維和創新思維，而不是像標準化考核中只關注問題的答案。

2 過程性評價公平的重要性

在過程性評價中，教學評價是被融入到每一次的教學過程中，與教學同步進行。盡管過程性評價的出發點是為了改善學生學習狀況，消除學生當前學習水平與教學目標間的差距，避免了學生平時松、考前忙、考后忘、用時慌的情況。但過程性評價是方方面面的，對學生學習的動機、效果、過程以及與學習密切相關的非智力因素進行全面評價[5]，這就需要教師付出大量艱辛的工作。

在運用過程性評價方法在教學過程中，每一位學生的情況都有所不同，表現不同;在團隊合作的項目中，每人對團隊的貢獻差別很大，但因為是團隊合作，每人分數又相同，要想公正，那么每人分數應該是不同的。以及有抄襲別人作業的同學和自己做的、有可能做錯的同學比，后者反而有可能獲得的分數更低。那么這樣打分，對那些遵守規則的學生就是極大的不公平！長此以往，不僅降低的這部分學生學習的積極性，同時給所有學生造成一個錯誤的認識，不利于學生形成正確的世界觀、人生觀。

所以如何給每個學生打分，使其分數反映的是每個學生自己的真實學習狀態，即如何打分對每個學生更公平，是需要急需解決的一個問題。

3 過程性考核的主要指標

本項目的研究對象是有學習《高等數學》的大一新生，過程性考核主要是由平時、實踐和期末測試組成。由于后兩項比較成熟，評價多數有比較客觀的標準，所以本項目主要討論的是平時分數。主要研究目標：使每個學生在過程性評價中獲得的平時分數，盡可能反映的是每個學生自己的真實學習狀況，減少渾水摸魚、濫竽充數的部分。平時分數主要由平時作業、課堂表現、出勤情況、自主學習、團隊合作等多個部分有機組成，相輔相成。

3.1 平時作業

（1）每節課每個學生理解掌握的要點，不是指課本上精確的定義，是指自己對知識點的理解;

（2）每章的思維導圖;

（3）每一章節后隨著教師復習知識點創做出相應知識點的題目。

3.2 課堂表現

（1）回答問題的次數和質量;

（2）睡覺、看手機等情況;

（3）在眾多人面前的表達能力：能否把一個數學問題表達清楚的能力;

（4）包裝能力：能否把復雜問題簡單表達，簡單問題抽象化。

3.3 出勤情況，結合傳統點名和信息化手段

（1）遲到;

（2）曠課;

（3）請假;

（4）早退。

3.4 自主學習，倡導學生利用多元化的渠道進行學習

（1）能否提出問題或對同學提出的問題作出解答;

（2）能否將一個新的知識點講解清楚;

（3）課后時間能否對一個專項問題的研究，例如數學上數獨、24點、一筆畫、最優問題、小學奧數、趣味數學等等，只要跟數學有關的問題即可。

3.5 團隊合作

（1）小組成員內分工情況;

（2）成果展示情況;

（3）溝通協調能力。

3.6 起點情況

學生剛入學時每人的基礎各不相同，因此前面指標應有所側重，不能一刀切。

4 建立模型及求解

上述已經將計算平時分的情況提煉出來主要指標，下面我們用層次分析法（Analytic Hierarchy Process）即定性與定量相結合的方法解決問題，它特別是可以將決策者的經驗判決給予量化。

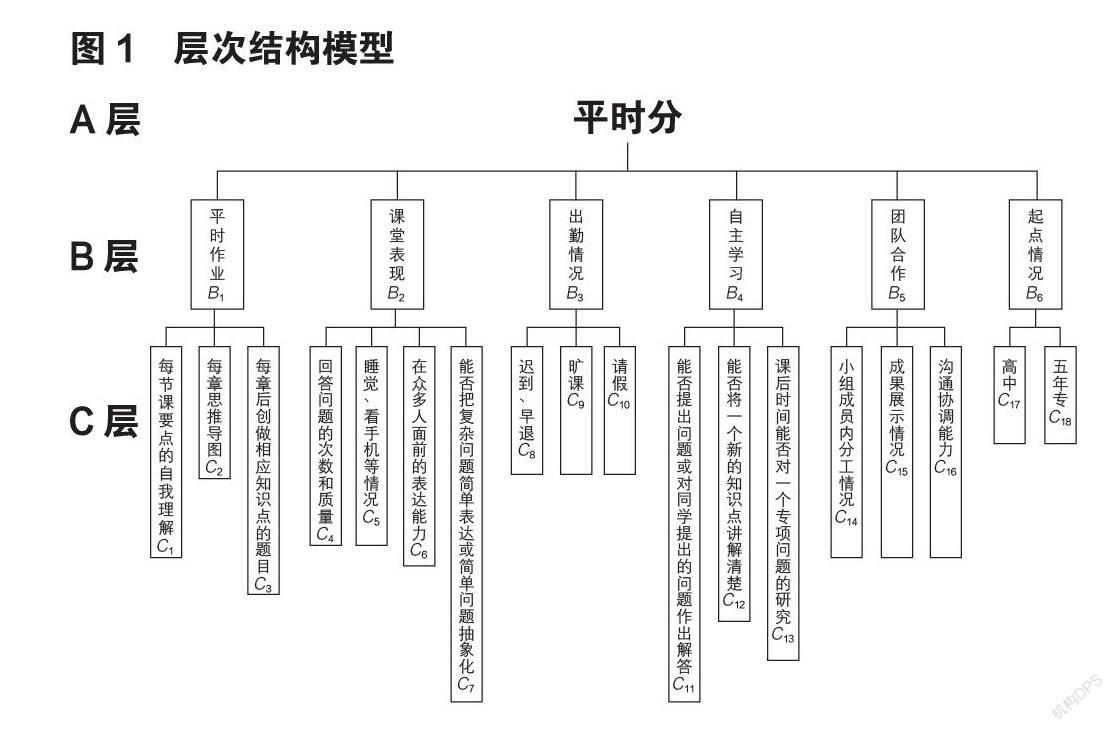
4.1 建立層次結構模型

本問題中，最上層為平時分，最下層為評價學生平時分時的各個子指標，中間層為評價學生平時分的幾個方面。因此可以建立層次結構模型，如圖1。

4.2 構造判斷矩陣，層次單排序及一致性檢驗

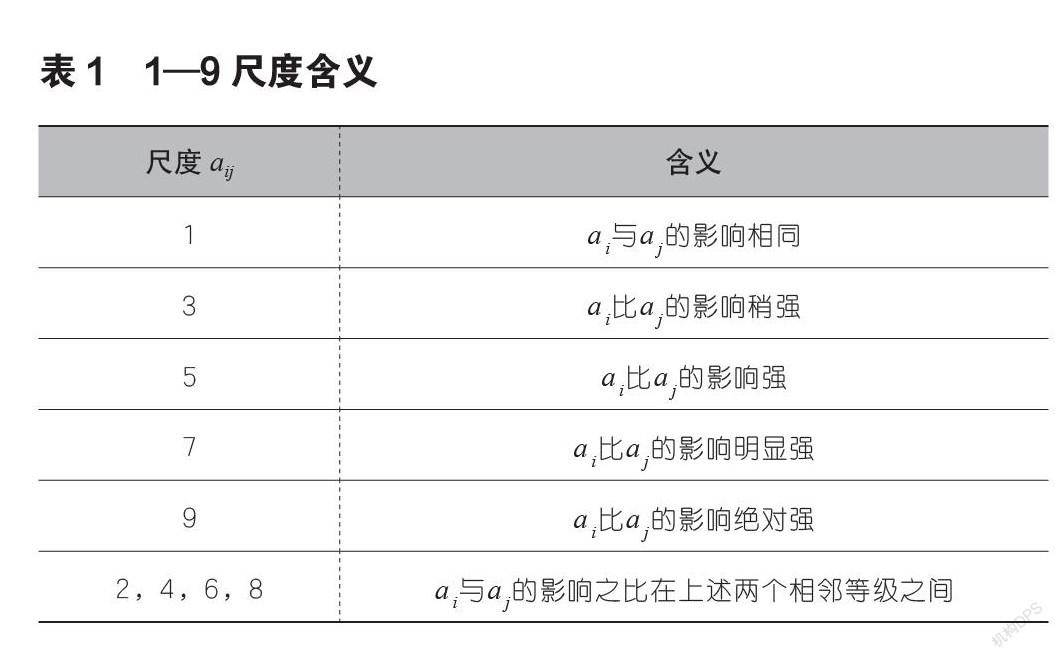
通過兩兩比較建立成對比較矩陣，利用Satty等人建議1～9尺度如表1，確定成對比較矩陣中的值，其最大特征值歸一化的特征向量為權重向量。

A-B層成對比較判斷矩陣：

經MATLAB計算可得最大特征值λmax=6.15，判斷矩陣的一致性指標CI=0.0336，可查表得隨機一致性指標RI =1.24，則隨機一致性比率，通過了一致性檢驗，接受矩陣A，對應于λmax的歸一化特征向量。

4.4 模型檢驗

我們使用本學院2020級報關班的學生情況，根據各指標的得分，通過我們的模型可計算出這個班學生的平時分，和期末測試進行對比如表3，Δh為通過模型計算出來的平時分的排名和學生期末測試成績排名的絕對差。

此數據可通過學校教務系統查詢，從表格中可看出根據模型計算出來的平時分和學生期末成績是正相關的，說明平時分的打分是相對公平的，反應了學生平時學習的情況。

基金項目：本文是福建省教育廳中青年教師教育科研項目《探討分析過程性評價中平時分的公平性》（編號：JAS19594）的研究成果。

參考文獻：

[1] 王莉，宿方萍，劉亞.過程性評價方法在高校文獻檢索課程教學中應用[J].教育現代化.2018（23）：227-229.

[2] 繆亞芹，張奕，李奇賀.關于過程性評價的兩個爭議及應對[J].教育教學論壇2018，（20）：133-134.

[3] 方穎玨，尹樂.離散數學的過程性評價探索[J].計算機教育2013，（22）：98-101.

[4] 郭孝存ISEC課程過程性評價方案的設計[J].福建電腦 2019，（7）：133-134.

[5] 鄭海波，郭元新，張繼武.過程性評價在應用型實驗課程教學中的應用[J].赤峰學院學報（自然科學版），2013，29（8）：194-196.

作者簡介：

尚利霞：（1979—），女，河南焦作市人，碩士，廈門海洋職業技術學院公共教育學院高等數學教師，講師。研究方向：基礎數學。