淺談數學課堂教學中科學探究精神的培養

王真紅

【摘 要】筆者在近幾年數學與科學的雙學科教學中，發現兩門學科均強調了科學探究精神的培養，而以科學課為甚。如果能在數學教學中借鑒科學課的做法，將會對學生科學探究精神的培養產生不小的影響，科學課的趣味性、探究性能啟示數學課科學地探究，從探究方案的設計到探究的過程再到探究結果的科學引領，均能幫助學生培養科學探究精神。

【關鍵詞】科學趣味 科學探究 學科素養

STEM教育緣起于美國，是“科學（Science）、技術（Technology）、工程（Engineering）、數學（Mathematics）”的縮寫。近年來，筆者參研了無錫市“十三五”規劃課題STEM教育研究，在大量的文獻學習與任教兩門學科的教學實踐中，發現兩門學科均強調了科學探究精神的培養，而以科學課為甚。如果能在數學教學中借鑒科學課的做法，將會對學生科學探究精神的培養產生不小的影響。筆者嘗試后發現：將兩門學科的優勢在教學中進行互補，會對學生的學習與學科的素養形成良性閉環。下面就來闡述“S（科學）”對“M（數學）”的教學啟示。

一、科學課的趣味性，啟示數學課科學地有趣

愛迪生說過，驚奇就是科學的種子。科學課的很多結論需要通過實驗才能得知，實驗前的相左猜測更能刺激學生的參與熱情，使學生興致盎然地期待著結果，并且意見相左的一方有時會保留對實驗結果的質疑權。反觀數學課，其結論的預見性比較好，學習能力強的學生能較準確地把握結果，就不那么期待過程，學生專注程度也沒科學課高。如果能讓學生在學習數學時也產生像上科學課時那樣濃厚的興趣，那么學生的數學學習情感定能得到良性的維系。

特級教師華應龍在參加完閱兵儀式后，設計了一節數學課“閱兵中的數學故事”。課上，學生積極參與，他們通過閱兵中的數學問題，經歷了問題解決的全過程，深刻地感受到“數字影響秩序、數學使人精細”。華應龍把它提升到“心中有數，無限美好”的境界！3個閱兵故事分別解決了3個不同的問題：“破解51之謎”解決了隊列的問題，同時發現整個隊伍具有左中右對稱的美，因為每列人數17和25都是單數（一人在最中間）。“為了神圣的那一刻”踢正步通過檢閱區，學生提出需要知道速度、檢閱區的長度及方隊的長度，其原型就是火車過橋問題;而算方隊的長度的原型就是植樹問題。“當坦克踩上俄軍的腳跟”類似追及問題，學生經歷了問題發現、問題分析之后，發現最終外國軍隊按中國步伐受閱，實際不存在追及問題，但卻很好地使知識得到了回顧。這類生活問題，如果在課本中能找到原型，就可以讓學生經歷問題解決的全過程，夯實發現問題、提出問題、分析問題和解決問題的基本功。

再如：特級教師許衛兵執教的“歌聲里的數學”、筆者執教的“冬至里的數學”等，都能借助課本中的原型，科學地提升學生數學學習的興趣。此外，課本上一些圖形直觀的例題，也可變成實物直觀，這樣既能增強趣味性，又易于學生理解算理。學生學習的興趣程度不同，效率當然也就迥然不同啦！

二、科學課的探究性，啟迪數學課科學地探究

筆者在兩門學科的教學實踐中發現，科學的探究過程更為完整、嚴密，更能培養學生問題解決的核心素養。而數學課，由于探究出規律后還要達到實際應用乃至靈活運用的程度，所以其探究環節往往比較匆忙，這是目前科學課能給數學課的最重要的啟示。

（一）科學課的方案設計，啟迪數學課科學地設計方案

科學課上，當學生觀察完實驗現象后，筆者都會引導學生猜測：“結果會是怎樣的？你的理由是什么？為什么會這么猜？”學生說出自己的猜想及理由后，筆者再問學生：“如何驗證你的猜想？”引導學生的思路走向實驗的方案設計;再加上其他學生的補充，一個比較科學、可能的準實驗方案就被設計出來了。而數學課上，學生的猜測出來后，教師一般會說，僅有猜測是不夠的，我們還需要小心求證，然后就會讓學生進入驗證環節。很少有教師問：“你打算怎樣驗證？”其實，驗證方案的科學設計，可以讓思維更為嚴謹，驗證的環節也更具典型性、更為簡便。教師不妨再追問下去：“有沒有需要考慮的特殊情況？在有限的時間內，你能不能更為簡捷地驗證出你的猜想？”第一個追問讓學生思考自己的猜想是否有前提條件或局限性，讓思維的嚴謹性“更上一層樓”;第二個問題引導學生選取典型數據，達到又快又好的驗證效果。

（二）科學課的實驗過程，啟迪數學課過程的科學性

達爾文說過，科學就是整理事實，以便從中得出普遍的規律或結論。科學課上，學生設計好方案后會帶著猜想進行驗證;驗證后如果發現新情況，便會進入新一輪的猜測與驗證中。這樣的科學課教學，踏上“觀察—猜想—驗證”的循環之路，并在實證中更加強調科學的方法，以保證實驗結果的客觀性。而在數學中，有時會因為結論的預知性，容易省略多次實證的環節，容易給人以特殊替代一般的錯覺。因此，科學課實驗的過程與方法是非常值得數學課借鑒的。

一位教師在教學五年級下冊“長方體和正方體的體積”一課時，以探究的方式學習體積公式，很好地展現了“觀察—猜想—驗證”的學習過程。當學生選擇用小方塊來研究長方體的體積后，教師引導學生說出自己的實驗設計后，讓學生進入研究環節。在反饋環節更是強化了驗證過程的科學性。第一小組的學生說自己研究的長方體體積是12立方厘米，教師追問：“你怎么得出這個結論的？”學生回答：“我是用小方塊來擺的，我用3個小方塊擺出了長方體的長，用兩排這樣的小方塊擺出了長方體的寬，這樣一層用掉了6個，我擺兩層擺出長方體的高，所以一共用了12個小方塊。”教師再追問：“你怎么知道是一樣的？”學生邊比較長方體和擺出的小方塊，邊說：“我用長來比一比，再用寬和高來比一比，都是一樣長的，所以長方體的體積和擺出的小方塊體積一樣大。”這時教師發出了第三問：“其他的長方體是不是一樣的？你又是怎樣研究的？”引導學生驗證結論的必然性。當得出長方體體積公式后，教師再次詢問：“現在大家知道長方體的體積是怎么算的了吧？”探究過程的四次發問，引導學生的研究逐步從或然走向必然，從特殊走向一般，尤其是“你怎么知道是一樣的”這樣的質疑追問，引領學生的思維走向嚴謹與嚴密。這樣的探究過程，充滿了科學性，也充滿了數學味。

（三）科學課的結論驗證，啟迪數學課科學地得出結論

科學課的實驗結論，有著或然性的特點，需要進行多次驗證，尋找其必然結果。對數學課而言，最大的啟發就是讓學生考慮結論的完備性，尤其是“0除外”之類的補充，這對學生的思維而言，顯得尤為珍貴。從學習的過程來看，這也是一個必經過程，學生一開始總是會得到大概的結論，如果沒有引導，容易誤以為就是最終結論了。如“釘子板上的多邊形”，學生在找完多邊形內部分別有1個釘子、2個釘子……n個釘子的規律后，會以為規律是分為兩類的，一類是內部沒有釘子的，一類是內部有釘子的。這時，教師引導學生思考：能不能把內部沒有釘子的情況也歸納到有釘子的情形中來呢？學生思考后就會發現是可以的，只要把-1看成+（-1）就可以了。這一結論的得出，不僅需要學生在知識上有一個完備性，更多的是需要思維上的反復思考與論證。數學結論的完整得出需要學生具有質疑的品質。

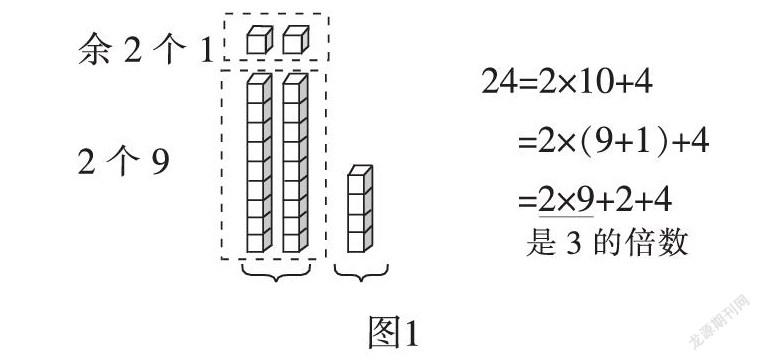
個人認為，科學地得出結論不僅僅體現在結論的完備性上，也體現在探究結論為什么會必然出現上，這會將學生的思維引向更深度的思考。如教學五年級下冊“3的倍數的特征”時，當學生找出特征后，教師發問：“為什么3的倍數的特征是這樣的呢？我們從圖上來看一看。”

圖中（如圖1）數與形完美地結合起來，將小方塊中是3的倍數的圈出來，讓學生直觀地看到：2個10中的每一個10都圈出了9個，這2個9一定是3的倍數不用再看了;還剩下2個，要和4個小方塊一起，看看是不是3的倍數。

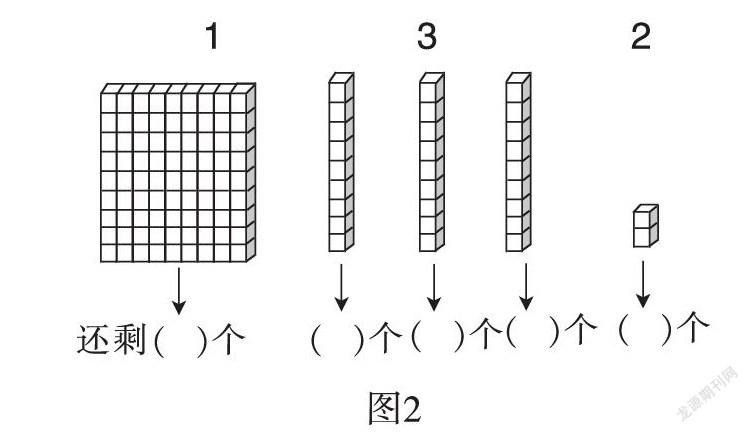
還有教師讓學生自己從圖中圈出3的倍數，圈完后填出各剩下幾個，再講解：這時是不是只要看剩下的幾個是不是3的倍數就可以了？（如圖2）

讓學生“知其然”，更“知其所以然”，這樣，探究學習會更深入，也會更有深度。如果能讓學生明白“何由以知其所以然”，知道教師是怎么想到的，那么探究學習將走向新的高度。

三、科學課的素養涵養，啟化數學素養科學地蘊養

小學科學課程標準提出，體驗科學探究的基本過程，培養良好的學習習慣，發展科學探究能力;發展學習能力、思維能力、實踐能力和創新能力，以及用科學語言與他人交流和溝通的能力等，從而培養出相應的科學素養。其中，對思維方式和學習習慣的要求、能力的要求，與小學數學課程標準是大同小異的。可見，科學素養的提高，從能力角度來說，可以視為科學地提高了學生的數學素養。科學課上培養起來的探索精神、質疑品質在數學學習方面亦是難能可貴的，學科素養的提升，必然會帶來學生綜合核心素養的提升。

在學習蘇教版科學六年級上冊第五單元“假設”和“實驗”這兩課時，學生真正進入了科學研究的樣態。學生在學習的過程中獲得了科學探究的方法，開啟了自主實驗之旅——選擇自己感興趣的內容進行模擬實驗或對比實驗，最終形成一個實驗報告。（部分學生實驗報告如圖3）

這些報告中，有的是模擬實驗，有的是對比實驗。在做非牛頓流體實驗時，學生在第一次玉米粉的實驗中，在水和粉的比是1：3成功之后，把這一經驗遷移到面粉、生粉與土豆粉中，發現不成功，于是分別做了水與面粉的比是1：1、1：2及2：1的實驗，最終發現面粉怎么做都不成功，生粉與土豆粉的比為1：1時，實驗基本成功，但效果不如玉米粉好！

科學實驗的過程中，學生發現問題，并重新設計實驗過程，通過多次的對比驗證得出了結論。學生追求真理，堅持用事實說話、用數據說理等科學素養在實驗過程中得到了培養。科學實驗極大地啟化著數學探究精神的素養蘊養，提升了學生的整體素質。當然，學科學習中能互相借鑒的地方還有很多。科學也好，數學也罷，及至其他的學科學習，都有各自的學科核心素養要培養，但一定可以互相借鑒，因為各學科素養的養成，最終將匯聚成學生綜合素養的養成。

注：本文系無錫市教育科學“十三五”規劃課題 “STEM教育研究”（課題編號：E/E/2018/002）的階段性研究成果。