數形結合思想在小學數學教學中的滲透與應用

凌建軍

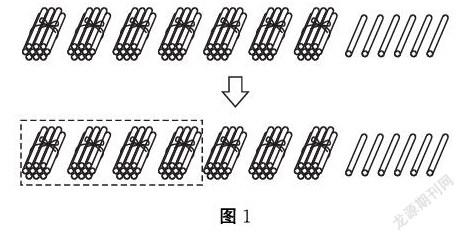
摘要：在數學教學中，數形結合是基本的數學思想之一，指的是將原本較為復雜的數理關系通過聯系可視化幾何圖形的方式來輔助理解或解答數學題的一種思想方法。小學數學中很多知識點對于學生來說理解起來相對較難，而數形結合思想的運用則可以有效降低知識理解和問題解答難度，因此數學教學中滲透和應用數形結合思想有助于提高教學質量，培養學生數學綜合能力。基于此，本文探討了數形結合思想的應用策略。

關鍵詞：數形結合思想 ?小學數學教學 ?應用策略

一、數形結合思想

在數學領域中，“數”和“形”是基本要素，二者能在恰當情況下進行轉化。其屬于數學思想方式，能細化分成兩種情景：利用精確性表示“形”的某類屬性;利用幾何直觀性表示數量關系。可用“數”解“形”，或者用“形”助“數”。而數形結合表示“數”和“形”的對應聯系，將抽象數量關系和幾何及位置對應關系進行結合，達到對復雜問題進行簡單化處理的目的，找出解題路徑。

二、數形結合思想應用于小學數學的重要作用

（一）降低學習難度

很多小學生之所以不喜歡數學，甚至產生抵觸心理，原因就在于感覺數學學習難度較大，知識理解和解題都存在很大局限。數形結合思想可以將數學知識轉變為生動靈活的圖像，讓學生看圖學數學，不僅降低了學習難度，同時也讓數學課堂學習變得更加生動有趣。

（二）培養學生的學習興趣

小學生對某一學科產生學習興趣是需要一定條件的，首先便是有趣，展現形式、教師語言、互動引導、教學內容、教學方法等都是影響學生興趣的關鍵，同時還有一項因素便是學習的難度。……