學(xué)生數(shù)學(xué)有序思維的培養(yǎng)探析
張燕美


[摘 要]數(shù)學(xué)思維是學(xué)生思維中的重要組成部分,有序思維則是數(shù)學(xué)思維品質(zhì)的獨(dú)特體現(xiàn)。教師在教學(xué)預(yù)設(shè)時(shí)立足“序”,在操作活動(dòng)中抓住“序”,在鞏固拓展中體現(xiàn)“序”,可讓學(xué)生在認(rèn)知結(jié)構(gòu)中構(gòu)建“序”,在知識(shí)結(jié)構(gòu)中生長“序”,在數(shù)學(xué)結(jié)構(gòu)中推進(jìn)“序”,在思想結(jié)構(gòu)中拓展“序”。
[關(guān)鍵詞]小學(xué)數(shù)學(xué);數(shù)學(xué)思維;有序思維
[中圖分類號(hào)] G623.5 [文獻(xiàn)標(biāo)識(shí)碼] A [文章編號(hào)] 1007-9068(2022)11-0081-03
現(xiàn)代數(shù)學(xué)與傳統(tǒng)數(shù)學(xué)有著本質(zhì)的區(qū)別,現(xiàn)代數(shù)學(xué)著重在教學(xué)過程中發(fā)展學(xué)生的思維,其中,學(xué)生思維方法的掌握是重中之重。有序思維是數(shù)學(xué)素養(yǎng)的核心,本文提出有序思維的培養(yǎng)意在通過探究學(xué)生思維中的“序”,找尋更科學(xué)的發(fā)展學(xué)生數(shù)學(xué)思維品質(zhì)的方式。
一、關(guān)于數(shù)學(xué)有序思維的部分闡述
有序思維,即解題有方法,思考有條理,是學(xué)生能夠按照既定的思維范式,遵循一定的邏輯順序,科學(xué)地選擇并運(yùn)用已形成的數(shù)學(xué)思想方法去觀察、思考、解決數(shù)學(xué)問題的一種綜合性的思維方式。
1.有序思維的意義
《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2011年版)》對(duì)小學(xué)階段學(xué)生的有序思維提出了基本要求——能進(jìn)行有條理的思考。由此可見,有序思維的培養(yǎng)是小學(xué)數(shù)學(xué)教學(xué)的要求。
我們知道,數(shù)學(xué)知識(shí)的發(fā)生及發(fā)展是有著其獨(dú)特的順序的。在教學(xué)過程中,我們要關(guān)注小學(xué)數(shù)學(xué)教材的編排體系,了解小學(xué)數(shù)學(xué)知識(shí)的前后聯(lián)系,如此才能在教學(xué)時(shí)有的放矢,讓學(xué)生充分經(jīng)歷知識(shí)的獲得過程。有序思維的培養(yǎng)是兒童認(rèn)知發(fā)展的需求,數(shù)學(xué)學(xué)科則是訓(xùn)練有序思維、構(gòu)建有序思維的優(yōu)秀平臺(tái)。小學(xué)階段如果能形成有序思維,學(xué)生就可以更科學(xué)、更系統(tǒng)、更高效地發(fā)展數(shù)學(xué)思維品質(zhì)。同時(shí),數(shù)學(xué)高階思維的培養(yǎng)離不開有序思維。有了有序思維,學(xué)生的思維才能由單一性變?yōu)槎嗝嫘裕傻碗A轉(zhuǎn)為高階,由記憶、理解、應(yīng)用升級(jí)為分析、綜合、評(píng)價(jià)和創(chuàng)造等,從而探究復(fù)雜的數(shù)學(xué)知識(shí)。
2.有序思維的特征
有序思維表現(xiàn)出四種基本的特征。
(1)程序性。思維的程序性表現(xiàn)為引導(dǎo)學(xué)生的思維由淺入深、由易到繁的過程。
(2)邏輯性。思維的邏輯性表現(xiàn)為在思維的形式、方法和過程中有理有據(jù)、有條不紊、層次鮮明、前后一致。如在“眾數(shù)”的教學(xué)中,筆者將例題的情境改為賣衣服:“觀察某品牌衣服的尺碼銷售圖(圖略),找出服裝店老板下一次應(yīng)進(jìn)貨最多的尺碼。”在經(jīng)過小組討論后,有學(xué)生提出選“中位數(shù)100”作為進(jìn)貨最多的尺碼,有學(xué)生選平均數(shù)105,還有學(xué)生選120(因?yàn)樵摮叽a賣出的最多,說明該身材的人最多)……在這個(gè)知識(shí)生長點(diǎn)上,學(xué)生的思維變得更有邏輯性。
(3)合理性。思維的合理性表現(xiàn)為嚴(yán)密的邏輯、正確的結(jié)論。具有合理性思維的學(xué)生,會(huì)用“言必有據(jù)”取代“以偏概全”“想當(dāng)然”,運(yùn)算和推理的每一步都有充分的理由。
(4)靈活性。思維的靈活性表現(xiàn)為對(duì)思維對(duì)象進(jìn)行全面的辯證評(píng)估,提出更符合實(shí)際情況的思維方法。如在計(jì)算[12]+[14]+[18]+[116]+[132]時(shí),有的學(xué)生運(yùn)用“通分”的方法,有的學(xué)生運(yùn)用畫圖的策略,還有的學(xué)生運(yùn)用“轉(zhuǎn)化”的途徑。
二、關(guān)于數(shù)學(xué)有序思維的培養(yǎng)途徑
“數(shù)學(xué)是思維的體操。”在小學(xué)數(shù)學(xué)課堂中,教師要注重有序思維的培養(yǎng),讓數(shù)學(xué)核心素養(yǎng)不斷提升。
1.在認(rèn)知結(jié)構(gòu)中構(gòu)建
數(shù)學(xué)的認(rèn)知結(jié)構(gòu),即學(xué)生頭腦中的數(shù)學(xué)知識(shí)是通過自己理解的廣度和深度,再結(jié)合自身的感知、思維等特征所形成的具有獨(dú)特的內(nèi)部規(guī)律的整體架構(gòu)。兒童的認(rèn)知發(fā)展具有階段性和順序性,教師要善于利用這種階段性和順序性,準(zhǔn)確把握兒童的認(rèn)知結(jié)構(gòu),開展有序思維的訓(xùn)練。
小學(xué)數(shù)學(xué)教材將“認(rèn)識(shí)分?jǐn)?shù)”的知識(shí)進(jìn)行了三個(gè)層次的編排:第一層次在三年級(jí)上冊(cè),設(shè)立的學(xué)習(xí)目標(biāo)是在情境中初步認(rèn)識(shí)分?jǐn)?shù),會(huì)讀寫分?jǐn)?shù)及其對(duì)應(yīng)的小數(shù),理解具體分?jǐn)?shù)在不同情境中的意義;第二層次在三年級(jí)下冊(cè),設(shè)立的學(xué)習(xí)目標(biāo)為進(jìn)一步認(rèn)識(shí)與探索分?jǐn)?shù)和小數(shù)之間的關(guān)系,并能熟練進(jìn)行分?jǐn)?shù)和小數(shù)的轉(zhuǎn)化;第三層次在五年級(jí),設(shè)立的學(xué)習(xí)目標(biāo)為建立單位“1”的概念,完善分?jǐn)?shù)的意義,認(rèn)識(shí)真假分?jǐn)?shù),熟練轉(zhuǎn)化分?jǐn)?shù)與除法、分?jǐn)?shù)與小數(shù)。三個(gè)層次的目標(biāo)各不相同、各有側(cè)重,三個(gè)層次的例題編排都遵循從直觀到抽象、從過程到結(jié)果的規(guī)律。教師要進(jìn)行有序的解讀,讓學(xué)生對(duì)分?jǐn)?shù)知識(shí)不斷重構(gòu)。如教學(xué)五年級(jí)的“認(rèn)識(shí)分?jǐn)?shù)”時(shí),筆者著重研究學(xué)生的“最近發(fā)展區(qū)”,了解他們已有的知識(shí)儲(chǔ)備和知識(shí)結(jié)構(gòu),確定三個(gè)教學(xué)程序。
(1)體會(huì),在觀察與對(duì)比中。讓學(xué)生自學(xué)例題,并給他們提出自學(xué)要求。
①說一說:每個(gè)圖形中的[14]表示把(? ? )看作一個(gè)整體,平均分成了(? ? )份,涂色部分表示這樣的(? ? )份。
②比一比:每個(gè)圖形中的異同。
通過對(duì)這兩個(gè)問題的探究,學(xué)生明白了“一個(gè)物體”或者“一些物體”都可以看作一個(gè)整體。
(2)設(shè)計(jì),在思考與操作中。單位“1”的概念必須建立在“有序”的操作中。對(duì)此,筆者設(shè)計(jì)了“創(chuàng)造分?jǐn)?shù)”的展示活動(dòng),讓學(xué)生自己創(chuàng)造一個(gè)分?jǐn)?shù),并介紹自己的創(chuàng)造過程,最后筆者將學(xué)生展示的分?jǐn)?shù)按照一定的標(biāo)準(zhǔn)進(jìn)行分類。將抽象的概念變成具體的圖形,不僅易于學(xué)生理解,還促進(jìn)了他們有序思維的發(fā)展。
(3)鞏固,在表達(dá)與訓(xùn)練中。表達(dá)是思維的載體。數(shù)學(xué)語言表達(dá)能力的培養(yǎng)實(shí)質(zhì)是學(xué)生分析問題與解決問題的能力的培養(yǎng)。在實(shí)際教學(xué)中,我們應(yīng)該堅(jiān)持在表達(dá)與訓(xùn)練中鞏固學(xué)生“有序”的數(shù)學(xué)思維,以便更有效地培養(yǎng)學(xué)生思維的準(zhǔn)確性、邏輯性。如筆者在學(xué)生掌握了分?jǐn)?shù)的完整概念之后安排鞏固階段,設(shè)計(jì)的練習(xí)不再局限于某個(gè)分?jǐn)?shù)的運(yùn)用訓(xùn)練,而是注重分?jǐn)?shù)在具體情境中的意義表述,尤其是抓住“單位1”“平均分”等關(guān)鍵詞進(jìn)行設(shè)計(jì)。
2.在知識(shí)結(jié)構(gòu)中生長
數(shù)學(xué)知識(shí)是有序的,但數(shù)學(xué)知識(shí)被分割成一個(gè)個(gè)知識(shí)點(diǎn)分散在教材中。作為小學(xué)數(shù)學(xué)教師,我們要對(duì)相同知識(shí)、相近知識(shí)、相鄰知識(shí)進(jìn)行系統(tǒng)梳理,從知識(shí)的板塊入手進(jìn)行概括直至形成框架,提高學(xué)生的結(jié)構(gòu)化意識(shí)。同時(shí),教師關(guān)注數(shù)學(xué)知識(shí)間的邏輯順序和邏輯結(jié)構(gòu),既可以幫助自己調(diào)整教學(xué)目標(biāo)、重難點(diǎn)的定位,又可以幫助學(xué)生轉(zhuǎn)變思維。
例如,在六年級(jí)數(shù)學(xué)總復(fù)習(xí)“數(shù)的運(yùn)算”中,可以引導(dǎo)學(xué)生勾畫思維導(dǎo)圖(圖略),梳理出“數(shù)的運(yùn)算”的五個(gè)主干——口算、估算、筆算的計(jì)算方法,計(jì)算工具,整數(shù)混合運(yùn)算,分?jǐn)?shù)混合運(yùn)算和小數(shù)混合運(yùn)算,最后從每個(gè)主干中延伸出若干分支。
(1)在思維導(dǎo)圖中完善。“數(shù)形結(jié)合百般好。”思維導(dǎo)圖能使各數(shù)學(xué)知識(shí)點(diǎn)之間的并聯(lián)關(guān)系、串聯(lián)關(guān)系以及從屬關(guān)系一目了然。思維導(dǎo)圖中的五大主干成為五個(gè)研究中心,并由此向外延伸出數(shù)百個(gè)知識(shí)點(diǎn),每個(gè)知識(shí)點(diǎn)又與中心遙相呼應(yīng)。點(diǎn)與點(diǎn)之間的聯(lián)系增強(qiáng)了學(xué)生的立體思維能力,體現(xiàn)出思維的層次性和聯(lián)想性。這些點(diǎn)就像放射狀的立體化神經(jīng)元,構(gòu)成了學(xué)生的數(shù)學(xué)知識(shí)寶庫。
(2)在思維框架中明晰。引導(dǎo)學(xué)生完善思維導(dǎo)圖就是在引導(dǎo)學(xué)生對(duì)思維框架進(jìn)行架構(gòu),讓看似復(fù)雜的知識(shí)點(diǎn)都緊緊地圍繞著“數(shù)的四則運(yùn)算”和“有序解決方法”的目標(biāo),便于學(xué)生對(duì)數(shù)學(xué)經(jīng)驗(yàn)進(jìn)行提取,豐富他們的體驗(yàn),形成有序的思維框架。
(3)在有序之美中展現(xiàn)。從中心點(diǎn)“數(shù)的運(yùn)算”向四面八方伸展,“枝干”由粗到細(xì),形成線條分明的板塊,構(gòu)成了一幅多角度的數(shù)學(xué)思維導(dǎo)圖。對(duì)照這樣的思維導(dǎo)圖,學(xué)生在復(fù)習(xí)中能專注從計(jì)算方法上去研究整數(shù)、分?jǐn)?shù)、小數(shù)之間的口算、估算和筆算,形成有序的數(shù)學(xué)思維。
3.在數(shù)學(xué)結(jié)構(gòu)中推進(jìn)
設(shè)計(jì)有效的數(shù)學(xué)問題可以引導(dǎo)學(xué)生主動(dòng)思考。小學(xué)階段的數(shù)學(xué)知識(shí)環(huán)環(huán)相扣,在看不見的主線的串聯(lián)下,于課堂中采用問題串,把相似的或相同的板塊內(nèi)容鏈接起來,推進(jìn)數(shù)學(xué)課堂教學(xué),最終建立起全面的認(rèn)知體系,從而加速學(xué)生有序思維的培養(yǎng)進(jìn)程。
(1)啟發(fā)式。“問題是探索的動(dòng)力。”任何知識(shí)的增長與科學(xué)的進(jìn)步離不開問題的提出。
例如,在教學(xué)“兩位數(shù)乘兩位數(shù)”的計(jì)算法則后,筆者設(shè)計(jì)了一道思考題:□□×□□=1200。并提出3個(gè)啟發(fā)式的問題。
①認(rèn)真觀察,在小組內(nèi)交流你的填法。
②在小組內(nèi)比較各填法的異同。
③如何不重復(fù)、不遺漏地寫出所有的可能?
啟發(fā)式的問題使小組內(nèi)的成員在分享中建構(gòu)有序的思維,填出所有的可能,從而感受到合作帶來的成就感。
(2)類推式。類推即比照某一事物的某個(gè)屬性或某種特征,推測出跟它同類的其他事物的屬性或特征。在類推式的問題串中,學(xué)生掌握了一定的研究思路,積累了此類問題的解決經(jīng)驗(yàn)后,數(shù)學(xué)思維就會(huì)由特殊轉(zhuǎn)向一般。
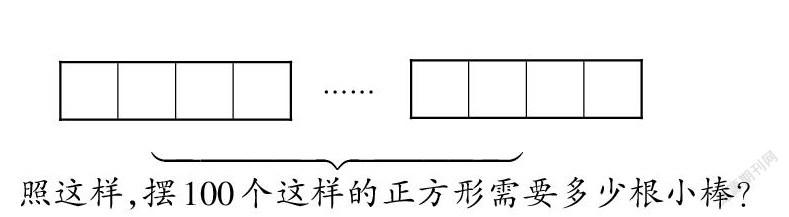
例如,在活動(dòng)課“探究圖形的規(guī)律”中(見下圖),筆者采用類推式的問題串讓學(xué)生感悟“當(dāng)掌握了某個(gè)問題的解決方法時(shí),此類問題我們也能順利解決”。
在研究的過程中,學(xué)生發(fā)現(xiàn)擺1個(gè)正方形需要4根小棒,以后每增加1個(gè)正方形就增加3根小棒,有三個(gè)解決方法:①4+(100-1)×3;②1+100×3;③100×4-99(100個(gè)正方形中有99根是共用的,需減去)。此時(shí),筆者提出類推式的問題:“照這樣,擺1000個(gè)正方形需要多少根小棒?照這樣,擺n個(gè)正方形需要多少根小棒?”學(xué)習(xí)能力強(qiáng)的學(xué)生會(huì)總結(jié)出“1+3n”的表達(dá)式。筆者接著提出:“如果把題目改成‘照這樣,擺n個(gè)三角形需要多少根小棒?擺n個(gè)正五邊形和擺n個(gè)正六邊形分別需要多少根小棒?’呢?”在舉一反三的問題中,筆者由“一個(gè)問題”轉(zhuǎn)為“一類問題”,將數(shù)學(xué)思想從特殊轉(zhuǎn)向一般,從淺顯邁向縱深。
4.在思想結(jié)構(gòu)中拓展
數(shù)學(xué)思想,即人們將現(xiàn)實(shí)世界的數(shù)學(xué)關(guān)系或數(shù)學(xué)理論通過思維活動(dòng)在意識(shí)中的反應(yīng)結(jié)果,它不同于數(shù)學(xué)的解題思想和方法。數(shù)學(xué)思想貫穿小學(xué)階段的數(shù)學(xué)學(xué)習(xí),為學(xué)生的數(shù)學(xué)知識(shí)、技能和素養(yǎng)的生長提供能量。筆者以“多邊形的面積”系列教學(xué)為例,從兩個(gè)方面滲透數(shù)學(xué)思想。
(1)數(shù)形結(jié)合。數(shù)學(xué)學(xué)習(xí)離不開數(shù)形結(jié)合,尤其是平面圖形的探究。在“平行四邊形的面積”的鞏固環(huán)節(jié),筆者設(shè)計(jì)一個(gè)問題:“一個(gè)平行四邊形相鄰兩條邊的長分別是3厘米和5厘米,高是4厘米,該平行四邊形的面積是多少?應(yīng)該用哪個(gè)數(shù)據(jù)做底呢?”筆者鼓勵(lì)學(xué)生在給出的平行四邊形(已經(jīng)標(biāo)注相鄰的邊的長度)中畫高,學(xué)生通過操作、反思和推理快速找出4厘米的高對(duì)應(yīng)的底。正是給思維插上數(shù)形結(jié)合的“翅膀”,學(xué)生才能在知識(shí)的高空中翱翔,幫助學(xué)生降低了解決問題的難度,加速了思考的過程,正所謂“一圖開路,思路皆來”。
(2)立足建模。建模思想是數(shù)學(xué)思想的核心之一,它是指人們?cè)诮鉀Q問題的過程中先逐步形成解決模式并建立數(shù)學(xué)模型,再通過數(shù)學(xué)模型去解決實(shí)際問題。在對(duì)已知信息的分析、處理與加工中,找出它們的出處和原型,有利于學(xué)生舉一反三、觸類旁通。在探究完長方形、正方形、平行四邊形的面積之后,學(xué)生逐步建立起“猜想→驗(yàn)證→結(jié)論”的平面(立體)圖形探究程式,在剪、移、拼、思、遷移中將平行四邊形轉(zhuǎn)化為面積相等的長方形,形成基本的模型,從而為以后探究三角形、梯形、圓等圖形的面積打下堅(jiān)實(shí)的基礎(chǔ),厘清數(shù)學(xué)思維的脈絡(luò)。
綜上所述,有序思維既能調(diào)動(dòng)學(xué)生主動(dòng)思考的興趣,又能激發(fā)創(chuàng)新思維。教師應(yīng)抓住學(xué)生認(rèn)知發(fā)展的規(guī)律,結(jié)合數(shù)學(xué)知識(shí)螺旋上升、循序漸進(jìn)的特征,充分認(rèn)識(shí)有序思維的價(jià)值,合理地、高效地發(fā)揮小學(xué)數(shù)學(xué)的學(xué)科特點(diǎn),探究有序思維的培養(yǎng)策略、培養(yǎng)方式和培養(yǎng)途徑,從而促進(jìn)數(shù)學(xué)素養(yǎng)的不斷豐盈。
(責(zé)編 覃小慧)

