基于信息獲取能力培養的應用題教學研究

卜凡紅

摘 要：高考應用題的命題多會滲透一些現實應用情景來填充題干，使題目與生活現實形成更加密切的聯系，學生可以從這類習題的解答中獲得能力的發展.本文圍繞信息獲取能力的培養對應用題解題教學做出了闡述.

關鍵詞：高中數學；信息獲取能力；應用題教學；審題

學生信息獲取能力的培養是現階段高中數學教師需要密切關注的一點，教師需要結合教學解析和解題教學的進行為學生解密解決相關綜合化習題的有效方法.在現階段，高考命題中信息獲取習題的占比有著較大的提升，除了應用題命題外，選擇題、填空題中也出現了很多相關的習題，這意味著高考對學生信息獲取能力的考查有了進一步的提升.為了推動學生的學習與發展，教師在實際中需要選擇代表性的應用題，并將部分選擇題和填空題改制為應用題，引領學生進行分析與思考，推動其綜合能力的提升.

1 選取合適例題，做出分析展示

有效例題的選取和展示是應用題解題教學的起始設計，教師可以在實際中選擇有代表性的應用題進行展現，推動學生做出分析與思考，進而幫助學生解讀應用題的構成.其中，為了引領學生初步認識考查信息獲取能力的實際應用題，教師需要利用課前時間進行研究分析，從學生的實際發展出發來做出展示過程的設計.在完成應用題的篩選后，教師可以根據應用題的主題和內容進行簡要分類，并選取有代表性的習題來做出展示.

例如，在實際中，為了幫助學生對信息獲取類的實際應用題加以認識，教師就可以選擇為學生展示實際的習題，筆者在教學中展示了如下例題.

例1 南水北調工程緩解了北方一些地區水資源短缺問題，其中一部分水蓄入某水庫，已知該水庫水位為海拔148.5m時，相應水面的面積為140km2；水位為海拔157.5m時，相應水面的面積為180km2.將該水庫在這兩個水位間的形狀看作一個棱臺，則該水庫水位從海拔148.5m上升到157.5m時，增加的水量約為多少呢？（7=2.65）

例2 某醫療團隊為研究某地的一種地方性疾病與當地居民的衛生習慣（衛生習慣分為良好和不夠良好兩類）的關系，在已患該疾病的病例中隨機調查了100例（稱為病例組），同時在未患該疾病的人群中隨機調查了100人（稱為對照組），得到如下數據：

在展示了上述兩道習題后，筆者便引導學生就兩道題目的共同特征進行觀察，分析這兩道題目與日常解題中常見的數學題存在哪些異同.在展示構成中，筆者使用多媒體分別演示就兩道習題中所摻雜的現實情境進行了解析.如針對例題一，筆者就南水北調做出了強調，引領學生思考這一題目的現實意義，在例題二中，則就衛生習慣和一些常見疾病的聯系進行了說明，并選取拓展閱讀供學生進行觀察與思考.在此基礎上對該題目相關的數學知識進行了解讀.

2 出示審題流程，推動學生嘗試

審題教學是應用題解題教學的關鍵，通過研究可以發現，很多學生對應用題的解答存在畏懼，其原因是學生缺乏有效解析應用題題干的能力，無法從應用題題干中獲取解題所需的基本信息，這使得其解題常常會陷入困境.在應用題解題教學中，教師需要重視審題讀題的開展，并設置有效的教學環節，引領學生嘗試著進行應用題審題和讀題.教師在學生進行初步研讀與思考后，選擇應用題解析讀題的基本方法，并引領學生進行思考與感悟.

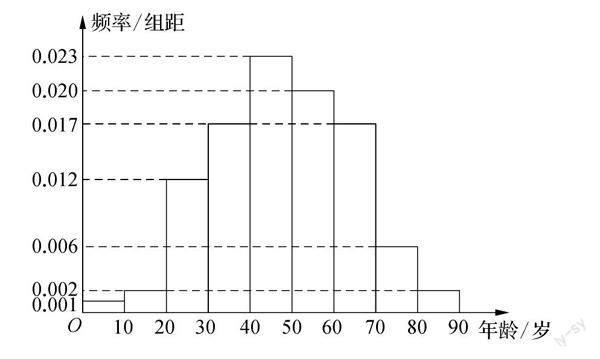
例3 在某地區進行流行病調查，隨機調查了100名某種疾病患者的年齡，得到如下的樣本數據頻率分布直方圖.

（1） 估計該地區這種疾病患者的平均年齡（同一組中的數據用該組區間的中點值代表）

（2） 估計該地區一人患這種疾病年齡在區間（20，70）的概率.

（3） 已知該地區這種疾病的患病率為0.1%，該地區的年齡位于區間［40，50）的人口占該地區總人口的16%，從該地區任選一人，若此人年齡位于區間［40，50），求此人患該種疾病的概率.（樣本數據中的患者年齡位于各地區的頻率作為患者年齡位于該區間的概率，精確到0.0001）

在展示了這一例題后，為了讓學生了解審題的基本流程，筆者就結合該題目的審題做出了介紹.其中筆者首先出示了審題的基本流程：題干閱讀——找出信息——確定內容——尋找關系——探尋問題——關系轉換.即要首先對題干進行閱讀，對題干中的信息進行瀏覽，尋找關鍵的解題信息，在確定了相關的信息后，再結合問題的問法去讀圖讀表，尋找與問題相對應的解題數據，最后再運用轉化的方法將實際問題轉換為數學問題.在完成了系統方法的解讀后，筆者便要求學生嘗試著運用上述方法對目標習題進行讀題，挑選出題目中的關鍵解題信息.學生通過解讀信息，得出了“100”“數據頻率分布直方圖”“0.001”“0.002”“0.006”“0.012”“0.017”“0.020”“0.023”等題干信息，而后再結合各個問題去題目中讀取相關聯的信息進行解題.

3 圍繞方法教學，進行過程解析

方法教學的合理進行也是應用題解題的重要環節，為了幫助學生掌握解答應用題的現實方法，教師需要結合例題的解析從應用題的題干解析、應用題內的條件關系解讀、應用題的列式解答三點入手做出解答過程的解析與展示，有效地推動學生進行分析與思考.

例4 現有一批產品需要進行質量檢驗，檢測的方法是先從這批產品中抽取4件進行檢查，將其中的優質品件數記為n，如果n=3，則再從該批次中抽取4件進行檢驗，若均為優質品，則視為該批次通過檢驗；如n=4，則需要再從該批次產品中取出1件進行檢驗，若均為優質品，則視為通過檢驗；當n的數值為其他數字，則都視為未通過檢驗.假設一批產品的優質品率為50%，此時取出產品是優勢品的概率均為1／2，且各件產品是否為優質品的概率相互獨立.

（ⅰ） 求這批產品通過檢驗的概率；

（ⅱ） 已知每件產品檢驗費用為100元，凡抽取的每件產品都需要檢驗，對這批產品做質量檢驗所需的費用記為x（單位：元），求x的分布列及數學期望.

解析：通過分析可以發現該題目考查離散型隨機變量及其分布列涉及數學期望的求解.在明確考查的知識內容后，便可以對該題目進行審題，找出題目中給出的產品抽樣的規律.在審題后可以發現，該批產品的優質率為50%，即可能出現n分別為1、2、3、4的情況，其中n=2的概率更高，當n出現等于3、4兩種數值的情況時，才有概率通過檢驗.在明確了該內容后，便可以根據實際情況進行解題.

5 引入變式題目，促進學生觀察

變式訓練是習題教學中的一個關鍵點，教師需要關注變式訓練的開展并圍繞學生的實際發展來做出構建.在教學中，教師要練習所教授的應用題內容來做出習題的變式調整，從學生的實際發展出發來進行綜合化的練習構建.基于此，教師可以選取一道有代表性的習題，對其進行變形處理，從題干、問題、提問方式三個方面調整題目的特征.

原題 小張和小劉約定本周日在16：00到17：00使用在線會議室進行項目進展的情況交流，假設兩人在這段時間內的每個時刻進入會議室是等可能的，先到者會等候另一人10分鐘，過時便會離去，那么兩個人在會議室內成功進行交流的概率是多少呢？

變式1 小張和小劉約定本周日在16：00到17：00使用在線會議室進行項目進展的情況交流，假設兩人在這段時間內的每個時刻進入會議室是等可能的，那么兩個人與16：30之前（包括16：30）在會議室內成功進行交流的概率是多少呢？

變式2 小張和小劉約定本周日在16：00到17：00使用在線會議室進行項目進展的情況交流，假設兩人在這段時間內的每個時刻進入會議室是等可能的，先到者會等候另一人10分鐘，過時便會離去，那么兩個人于16：30之后在會議室內成功進行交流的概率是多少呢？

6 開展展學活動，實施學生展學

展學活動的開展是推動學生解題能力提升的一個有效措施，教師在實際中要結合學生展學的構建來設置相關的活動.在現階段的教學中，教師可以圍繞應用題解題教學來設置學生展學活動，讓學生在活動中展示自己對于應用題解答的理解和思路.

實際中，為了構建應用題解題教學，推動學生的綜合發展，教師就可以將信息獲取能力作為核心進行設計，從例題分析、審題教學、方法教學、聯系設置、習題變式、學生展學六個方向做出構建.

參考文獻：

［1］ 崔明旭.分析高中數學應用題解題訓練策略的思考［J］.祖國，2018（7）：210.

［2］ 王慶寧.高中數學應用題的題型及解答技巧［J］.語數外學習（高中版中旬），2018（11）：37.