學習進階下高中數學單元復習課授課設計

黃偉杰

【摘 ?要】本文以高中數學中的重要內容——“圓錐曲線”（人教版B版）為例，探討如何進行單元復習課的授課設計.首先，對圓錐曲線的基本特點進行分析，明確其具有系統性和綜合性，并結合新課標素質教育的引領性要求，從知識技能和思想方法（或者學科素養）兩個方面，進行由低到高、由易到難的階梯式設計.希望能夠為各位教育同仁在進行圓錐曲線，乃至高中數學其他教學內容的單元復習課授課設計時，提供些許思路.

【關鍵詞】高中數學；圓錐曲線；單元復習課

圓錐曲線是高中數學中的重點內容之一，不論是在教學課時安排，還是在教學結果考核中，都占據了很大的比重.就圓錐曲線的內容來看，其一方面表現出了顯著的系統性，另一方面表現出了極強的綜合性.因此，在圓錐曲線部分的授課設計中，特別是在單元復習課的授課設計中，就需要特別注意兼顧圓錐曲線的知識技能和思想方法（或者學科素養），并在基礎足夠扎實的前提下，適當向思想方法（或者學科素養）方面傾斜，通過實施更加全面有效的教學策略，提高單元復習的效果.所以，研究和分析圓錐曲線的單元復習課的授課設計是有必要的，也是有價值的.

單元復習課是有利于幫助學生在總體方向上對已學知識進行把握的教學環節，將知識點向著知識線和知識面的方向進行推進，在規劃“大框架”“大思路”“大背景”的前提下，提升學生解決“大問題”的能力，通過全面統領、思維駕馭、結構關聯的方式，杜絕傳統教學模式下，知識零散、分解過度、效益低下的問題，并促進學生思想方法和學科素養的綜合提升.在新課程目標核心素養的引領下，對單元復習課的授課設計進行完善，從明確教學目標開始，使授課成為相互支撐和聯系的穩固體系，對于提高教學效果，特別是對于圓錐曲線內容的教學效果十分有益.

1 ?圓錐曲線的基本特點分析

結合實際教學活動，對圓錐曲線進行分析，認為其具有兩個基本特點.

一是系統性強.圓錐曲線包括橢圓、拋物線和雙曲線三個部分，每個部分都分別依次學習定義、性質、方程、函數圖象等內容，脈絡十分清晰.例如，在方程中，雖然圓錐曲線包括三個部分，但是總體來看，圓錐曲線的方程都滿足的二次方程的形式，具有一般性規律.其中，橢圓、拋物線和雙曲線具有各自不同的特殊性規律.這種特殊性規律是建立在一般性規律之上的.以橢圓為例，在圓錐曲線的方程中，當，，，，，時，就得到橢圓的方程，即橢圓方程滿足（a>b>?0，c>?0）的二次方程的形式.此外，拋物線和雙曲線方程也是圓錐曲線方程的特殊化形式，都是特殊的二次方程的形式.因此，圓錐曲線部分內容脈絡十分清晰.

二是綜合性強.圓錐曲線涵蓋的內容比較多，如上文所述，橫向涉及橢圓、拋物線和雙曲線三個部分內容，縱向涉及定義、性質、方程、函數圖象等部分內容，知識內容比較綜合.另外，圓錐曲線題目覆蓋比較雜，且通常不是直接出現，而是與其他知識進行聯合，例如，圓錐曲線方程與直線方程進行聯合等，解題方法比較綜合.總之，圓錐曲線在知識和題目兩個方面，都表現出了很強的綜合性.

2 ?圓錐曲線的單元復習課授課設計

在現行高中數學人教版B版教材中，圓錐曲線單元包括橢圓、雙曲線、拋物線，各部分之間的知識聯系有比較強的統一性，各部分之內的知識結構有比較強的相似性.這種統一性和相似性相既表現在知識技能方面，也表現在思想方法（或者學科素養）方面.單元復習課的授課設計可以根據圓錐曲線單元的統一性和相似性，采用了“總－分－總”的形式^[1]，圍繞知識技能主題或者思想方法（或者學科素養）主題^[2]進行單元總結回顧，形成完備的圓錐曲線學習與研究的大框架.具體的單元復習課授課設計如下：

2.1 ?基于知識技能為主題的單元復習課的整體設計

2.1.1 ?分析具體概念

圓錐曲線的定義作為該單元內容的開篇，至關重要.以圓錐曲線的定義為例，在復習課授課設計中，要基于圓錐曲線的定義（丹德林雙球模型）作出全面的分析，從文字表述、數學關系、幾何圖形等方面，綜合認識圓錐曲線.例如，從文字表述方面，圓錐曲線是到定點距離比到直線距離為常數e的軌跡；從數學關系方面，圓錐曲線是二次方程的圖象；從幾何圖形方面，圓錐曲線是用平面對圓錐面進行橫截地得到的交線.上述三個方面分別來看，當e的取值范圍不同；當二次方程系數不同；當平面橫截角度不同，可以分別得到橢圓、拋物線和雙曲線.此外，退化曲線與上述三類曲線不同，但也符合圓錐曲線的定義要求，需要特殊對待.

基于以上內容，為了能夠充分發揮復習課的作用，在分析具體概念時，要注意進行橫向的比較和縱向的聯合，使學生明確界定和準確判斷圓錐曲線的概念和性質，并且在解題的過程中，能夠借助理解記憶，發散思維，靈活應用.這將有利于學生在獲得數學基礎知識、基本技能、基本思想、基本活動經驗（簡稱“四基”）^[2]的過程中打好基礎，用好載體.

2.1.2 ?總結規律特點

圓錐曲線的內容具有明顯的系統性，其規律在新課授課的過程中表現不突出，但是在復習課授課的過程中表現非常明顯.以圓錐曲線的規律和特點^[4]為例，在復習課授課設計中，要善于總結規律和特點，結合上述關于圓錐曲線基本特點（系統性和綜合性）的分析可以得知，抓住規律就是抓住主線、抓住重點，能夠發揮提綱挈領，“牽一發而動全身”的作用.

總結規律特點可以從兩方面進行，一是從基礎定義入手，橢圓、拋物線、雙曲線的定義表現出了明顯的規律性，它們是圓錐曲線定義范疇下，不同的變換場景，既有密切的關聯，又有各自的特點，既有一般規律，又有特殊規律；二是從解題分析入手，在圓錐曲線的解題應用情景中總結規律特點，教師可以有針對性地提供既有聯系又有區別的練習題類型，并在解題之后總結解題方法，歸納解題思路，從而間接地認識圓錐曲線的規律特點.經教學實踐，發現不論是從基礎定義入手，還是從解題分析入手，都能獲得比較好的知識技能提升效果，教師可以根據實際進行具體選擇，解題提升復習課效果.

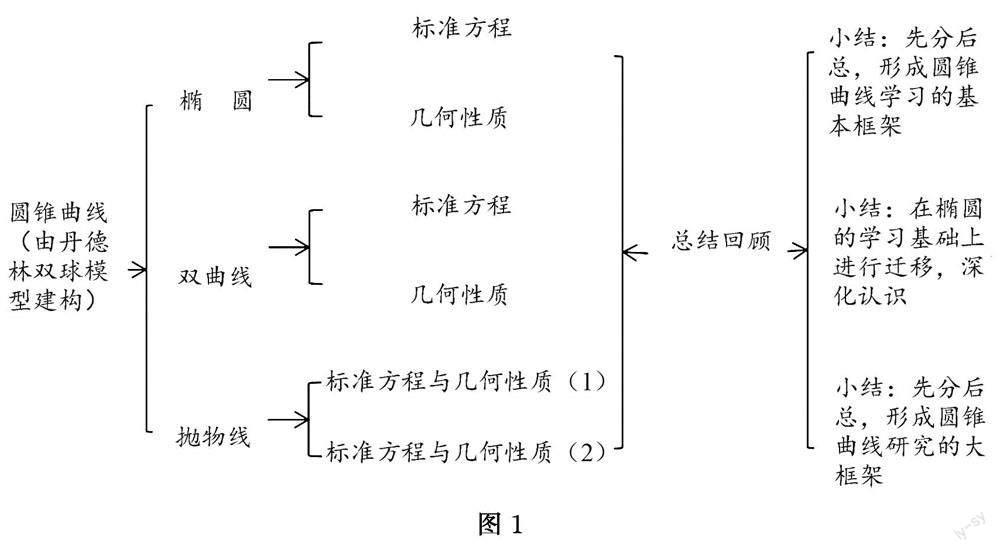
例如 ?在圓錐曲線單元復習課的授課設計中，從基礎定義入手，總結規律特點.一是“總”，基于丹德林雙球模型，引出圓錐曲線的定義，以及橢圓、拋物線、雙曲線的定義；二是“分”，分別對比總結橢圓、拋物線、雙曲線的標準方程和幾何性質；三是“總”，通過橫向遷移，建構知識內容大框架.

一般的，在單元復習課中，知識點是“明點”，知識線是“暗線”，在“明點”的基礎上梳理“暗線”，能夠運用辯證統一的方法，層層遞進，上位理解和深刻認識單元內容，建構系統的知識內容大框架（圖1）.

2.2 ?基于思想方法（或者學科素養）為主題的單元復習課的整體設計

2.2.1 ?培養數形結合思維

數學思維和數學方法是數學學習的核心重點.學生在新課授課中已經完成了基礎知識的學習，在單元復習課授課設計中，可以適當地向思想方法（或者學科素養）方面傾斜，借助邏輯和思維的引領作用，從大局上重新認識單元內容，從而推動學生的數學學習進階，提升學科素養的.在圓錐曲線的復習課授課設計中，考慮到圓錐曲線既包括二次方程（二次函數），又包括幾何圖象，并且在解題過程中，經常出現函數與幾何結合的情況，因此，可以從數形結合思維角度切入，以思想方法（或者學科素養）為主題，進行單元復習課授課.函數的有抽象性，幾何具有具象性，將函數和幾何進行融合，就是利用數形結合的思維，實現抽象問題的具象轉化的過程.經過具象轉化后的問題，還可以與向量、三角函數等內容進行進一步融合，從而在大背景下，培養學生的數形結合思維.

2.2.2 ?積累題目解決經驗

中數學教學內容具有明確范圍，積累解題經驗十分必要，其目標有兩項，其中，初級目標是在遇到同一題目時，能夠保證解題正確率；高級目標是在遇到同類型題目時，能夠實現知識遷移.通過回顧總結，不僅能夠幫助學生提高學習效果，還能夠幫助學生養成良好的思維模式和學習習慣.為此，以圓錐曲線的回顧總結為例，建議盡量適用圖表或者思維導圖的方式，例如，在表1中，根據所給的信息填空，能夠提高記憶和方便查閱，為將來的經驗應用提供便捷.

3 ?結語

綜上所述，在圓錐曲線的單元復習課授課設計中，需要在明確圓錐曲線的基本系統性和綜合性特點的基礎之上，從兩個方面入手，一是從基于知識技能為主題的單元復習課的整體設計入手，分析具體概念和總結規律特點，二是從基于思想方法或學科素養為主題的單元復習課的整體設計入手，培養數形結合思維和積累題目解決經驗，從而幫助發揮單元復習課的作用，在科學的誰授課設計引導下提高學生的復習實效.

參考文獻：

[1]張雪娟.思維可視化在圓錐曲線復習教學中的實驗研究[D].昆明：云南師范大學，2017.

[2]曾誠彥.高中數學圓錐曲線教學方法的創新研究[J].中學課程輔導（教師通訊），2018（11）：122.

[3]于龍.基于數學思想方法的高三專題復習——以運用圓錐曲線的定義解題為例[J].中國現代教育裝備，2017（04）：54-56.

[4]張瑋.高中數學圓錐曲線教學的有效性策略探討[J].數學學習與研究，2017（07）：56.