運用綜合解題思路解答多項選擇題的探索

錢寧

摘要：所謂綜合解題思路，就是面對難度較大的多項選擇題時，要集中聯系、分析、判斷、推理于一體，以某一種解題方法為主，同時綜合運用比較、計算、作圖、驗證、排除等多種方法，以達到“準確、快速、靈活、巧妙”解題的目的.

關鍵詞：數形結合法；公式計算法；各個擊破法；綜合處理

選擇題具有“小巧靈活、概括性強、知識覆蓋面廣、考查容量大、數學思想豐富、解題思路廣、有一定的綜合性與深度”等特點[1]，是每年高考的重點題型，在高考試卷中數量大，占分比例高，全國卷和部分自主命題省份的高考試卷中選擇題占60分（單項選擇題40分，多項選擇題20分）.其中，多項選擇題是近年來全國高考卷中出現的一種新題型，以2022年新高考卷為例，共設4個小題，每小題5分，共20分；在每小題給出的A，B，C，D四個選項中，有多項符合題目的要求，要全部選對才能得5分，部分選對只能得2分，只要有一項選錯就不得分（0分）.在單項選擇題中，只需要在四個選項中選一個正確答案即可，而在多項選擇題中，要在四個選項中，選出多個答案，而且要全部選對才能得滿分.從上述的給分標準和答題的要求來看，其難度可窺見一斑！當然，無論是從試題的整體難度、選項的迷惑性，還是從篩選的復雜性等相比較，多項選擇題的解答遠比單項選擇題麻煩，難怪許多考生面對多項選擇題會發出“得分不易失分易”的槪嘆.

不管是單選題還是多選題，它們都是選擇題，其解法既有區別又有聯系.當然，解答一些較復雜的多選題時，往往需要綜合運用幾種方法.下面重點探索如何運用綜合解題的思路來解答多項選擇題.

1 數形結合法

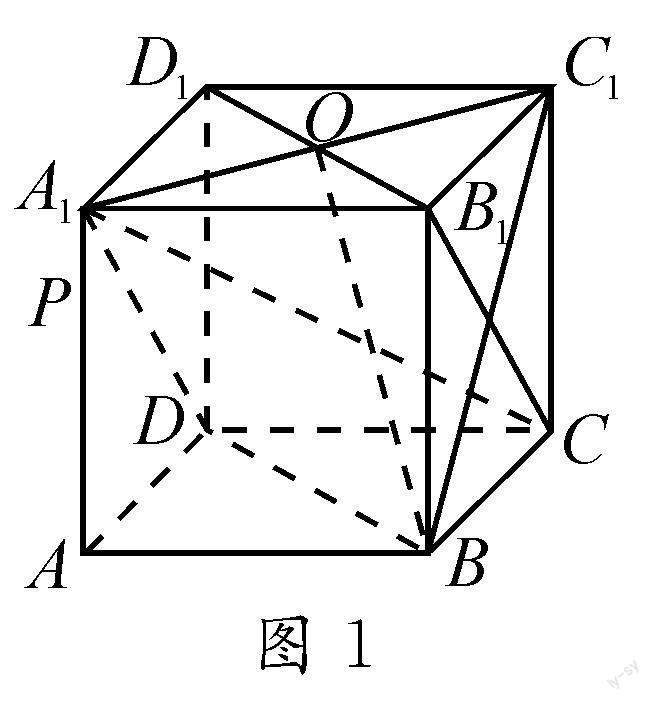
例1 （2022年新高考Ⅰ卷第9題）已知正方體ABCD-A1B1C1D1，則（）.

A.直線BC1與DA1所成的角為90°

B.直線BC1與CA1所成的角為90°

C.直線BC1與平面BB1D1D所成的角為45°

D.直線BC1與平面ABCD所成的角為45°

解析：如圖1，連接B1C，BC1.因為DA1∥B1C，所以直線BC1與B1C所成的角即為直線BC1與DA1所成的角.因為四邊形BB1C1C為正方形，則B1C⊥BC1，所以直線BC1與DA1所成的角為90°.

故選項A正確.

連接A1C，因為A1B1⊥平面BB1C1C，BC1平面BB1C1C，所以A1B1⊥BC1.

因為B1C⊥BC1，A1B1∩B1C=B1，所以BC1⊥平面A1B1C.又A1C平面A1B1C，所以BC1⊥CA1.

故選項B正確.

連接A1C1，設A1C1∩B1D1=O，連接BO.

因為BB1⊥平面A1B1C1D1，C1O平面A1B1C1D1，所以C1O⊥B1B.又C1O⊥B1D1，B1D1∩B1B=B1，所以C1O⊥平面BB1D1D.

因為C1C⊥平面ABCD，所以∠C1BC為直線BC1與平面ABCD所成的角，易知∠C1BC=45°.

故選項D正確.

故本題答案應選：A，B，D.

方法探索：以數形結合法為主，充分利用立體幾何知識，通過作圖、分析圖形，綜合使用觀察、對比、驗證、排除等方法依次對照選項進行篩選判斷.

2 公式計算法

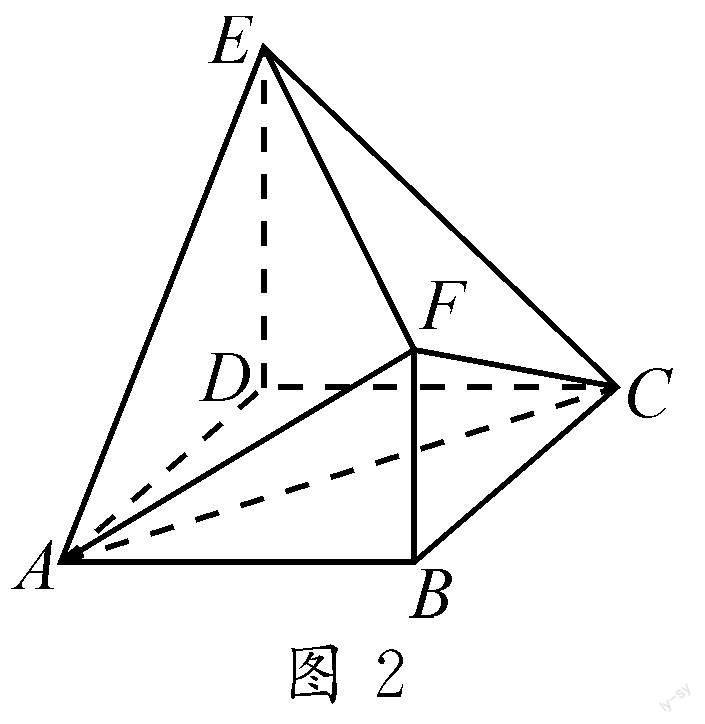
例2 （2022年新高考Ⅱ卷第11題）如圖2，四邊形ABCD為正方形，ED⊥平面ABCD，FB∥ED，AB=ED=2FB，記三棱錐E-ACD，F-ABC，F-ACE的體積分別為V1，V2，V3，則（）.

A.V3=2V2

B.V3=2V1

C.V3=V1+V2

D.2V3=3V1

解析：如圖3，設AB=ED=2FB=2a，因為ED⊥平面ABCD，FB∥ED，所以

連接BD，交AC于點M，連接EM，FM，可知BD⊥AC.又因為ED⊥平面ABCD，AC平面ABCD，所以ED⊥AC.又ED∩BD=D，ED，BD平面BDEF，所以AC⊥平面BDEF.

綜上，2V3=3V1，V3=3V2，V3=V1+V2.

把上述計算的結果與選項逐一對照，發現選項A，B錯誤，選項C，D正確.故本題答案應選：C，D.

方法探索：本題主要采用以三棱錐的體積計算結果與選項對照的方法進行判斷，求解過程中還綜合運用了作圖（添加輔助線）、觀察、證明、對照比較等方法.

3 各個擊破法

例3 （2022年新高考Ⅰ卷第10題）已知函數f（x）=x3-x+1，則（）.

A.f（x）有兩個極值點

B.f（x）有三個零點

C.點（0，1）是曲線y=f（x）的對稱中心

D.直線y=2x是曲線y=f（x）的切線

解析：根據題意可知，f′（x）=3x2-1.令f′（x）>

令h（x）=x3-x，該函數的定義域為[WTHZ]R[WTBX]，h（-x）=（-x）3-（-x）=-x3+x=-h（x），

則h（x）是奇函數，點（0，0）是h（x）的對稱中心.

將h（x）的圖象向上移動一個單位得到f（x）的圖象，所以點（0，1）是曲線y=f（x）的對稱中心.故選項C正確.

令f′（x）=3x2-1=2，可得x=±1.又f（1）=f（-1）=1，則當切點為（1，1）時，切線方程為y=2x-1；當切點為（-1，1）時，切線方程為y=2x+3.故選項D錯誤，排除.

故本題答案應選：A，C.

方法探索：本題綜合應用了定義法、比較法、驗證法、代入法、分析法、排除法等多種方法，采用各個擊破的策略，一種方法解決一個選項.首先根據極值點的定義判斷A選項正確；再結合函數f（x）的單調性、極值等判斷B選項錯誤；利用函數圖象的平移判斷C選項正確；根據導數的幾何意義得出切線方程判斷D選項錯誤.

從上述的解題探索中可以看出，多項選擇題由于涉及到的知識點多，很難用單純的某一種方法去解答，很多情況下需要運用綜合處理的解題思路，直接方法與間接方法相結合，幾種方法交替或同時并用[2]，這樣才有可能達到“又快又準”“小題小做”的目的.

參考文獻：

[1]歐陽群壯.高考數學選擇題的解答方法與技巧探析[J].中學教學參考，2016（23）：28，103.

[2]杜雨軒.試析考試中如何快速解答高中數學選擇題[J].數理化解題研究，2017（19）：29-30.