數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用

黃培勝

【摘要】數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用，具有降低學(xué)生學(xué)習(xí)難度、培養(yǎng)學(xué)生數(shù)學(xué)興趣與思維、幫助學(xué)生解決問題等優(yōu)勢.教師應(yīng)基于觀察性原則與操作性原則，應(yīng)用數(shù)形結(jié)合思想優(yōu)化小學(xué)數(shù)學(xué)教學(xué)模式，以便促進學(xué)生的進步與發(fā)展.文章以人教版小學(xué)數(shù)學(xué)教材為參考，舉例說明數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的具體應(yīng)用：教師應(yīng)在理解教材和關(guān)注生活的基礎(chǔ)上規(guī)劃教學(xué)，把握學(xué)生建立概念、理解和解決問題的時機，靈活應(yīng)用數(shù)形結(jié)合思想.

【關(guān)鍵詞】小學(xué)數(shù)學(xué)；數(shù)形結(jié)合；教學(xué)應(yīng)用

“數(shù)”與“形”是數(shù)學(xué)中兩個最古老的研究對象，故而在數(shù)學(xué)研究過程中，許多數(shù)學(xué)家提出數(shù)形結(jié)合思想：借助“數(shù)”的精確性闡明“形”的某些屬性，同時借助“形”的直觀性說明“數(shù)”的某種關(guān)系.目前，數(shù)形結(jié)合已經(jīng)成為最重要的數(shù)學(xué)思想之一，并且被廣泛應(yīng)用于小學(xué)數(shù)學(xué)教學(xué).教師應(yīng)基于小學(xué)階段數(shù)學(xué)知識特點與學(xué)生思維特點，準確把握數(shù)形結(jié)合思想在實際教學(xué)中的應(yīng)用原則，利用數(shù)形結(jié)合促使學(xué)生簡單、輕松、高效地學(xué)習(xí)，同時在學(xué)生心中埋下數(shù)學(xué)思想的種子.

一、數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用原則

（一）觀察性原則

小學(xué)階段的學(xué)生由于缺乏數(shù)形結(jié)合經(jīng)驗，較難在學(xué)習(xí)過程中快速形成數(shù)形結(jié)合思想，觀察是改善此情況的有效手段.教師應(yīng)基于觀察性原則為學(xué)生提供豐富的圖形（包括數(shù)學(xué)圖形與生活圖形），指導(dǎo)學(xué)生多角度、全方位地觀察圖形與幾何中的數(shù)與代數(shù)，使教學(xué)生動活潑，幫助學(xué)生發(fā)現(xiàn)“數(shù)”與“形”的內(nèi)在聯(lián)系，培養(yǎng)學(xué)生在形象元素中抽象出數(shù)學(xué)信息的能力，文章因此強調(diào)觀察性原則.教師應(yīng)以“看圖”為數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用基礎(chǔ).

（二）操作性原則

在對數(shù)學(xué)圖形與生活圖形的充分觀察中，學(xué)生基本上能夠形成一定的數(shù)形結(jié)合思想.此時，其數(shù)形結(jié)合學(xué)習(xí)不再滿足于看圖，而是提出畫圖需求.教師應(yīng)基于操作性原則滿足其需求，鼓勵學(xué)生自主畫圖.畫圖期間，學(xué)生自覺在“數(shù)”與“形”之間轉(zhuǎn)化，自主分析數(shù)形結(jié)合的最佳形式，這也是鍛煉其數(shù)形結(jié)合能力的重中之重.因此，教師應(yīng)以“畫圖”為數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用核心.

二、數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用

（一）理解教材，挖掘和整理數(shù)形結(jié)合元素

教材是最關(guān)鍵但不唯一的教學(xué)資源，任何模式的小學(xué)數(shù)學(xué)教學(xué)，都需要貫徹“教材本位”思想.人教版教材作為當前小學(xué)數(shù)學(xué)教學(xué)最常用的教材之一，內(nèi)容經(jīng)常呈現(xiàn)數(shù)形結(jié)合特征，故而有助于數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用.教師應(yīng)理解教材，預(yù)先挖掘、整理其中的數(shù)形結(jié)合元素，以便在實際教學(xué)中準確把握數(shù)形結(jié)合切入點.

比如二年級上冊“100以內(nèi)的加法和減法（二）”這一課，教材在“不進位加”“進位加”等內(nèi)容中設(shè)計大量示意圖，通過“小棒”“圓點”等圖形的直觀變化反映“數(shù)”的變化，意圖使學(xué)生抽象出運算規(guī)律；三年級下冊“面積”這一課，教材在“長方形、正方形面積的計算”中，借助“15個1平方厘米的正方形”“每行擺5個1平方厘米的正方形，一共擺3行”等“數(shù)”揭示圖形面積，意圖以“數(shù)”促進學(xué)生對“形”的學(xué)習(xí)；五年級上冊“簡易方程”這一課，教材在“練習(xí)十五”中多次使用線段圖，意在借助圖形的直觀性，指導(dǎo)學(xué)生準確理解數(shù)的意義和分析數(shù)量關(guān)系.從低年級到高年級，教材在不同學(xué)段均設(shè)置了大量數(shù)形結(jié)合元素，教師應(yīng)在實際教學(xué)備課階段，全面地梳理教材，理解其中的數(shù)形結(jié)合內(nèi)涵，從而貫徹教材理念，將數(shù)形結(jié)合思想按照教材意圖應(yīng)用于小學(xué)數(shù)學(xué)教學(xué)中.

（二）關(guān)注生活，收集和應(yīng)用數(shù)形結(jié)合資源

生活也是重要的教學(xué)資源，教師應(yīng)在以教材為基礎(chǔ)的小學(xué)數(shù)學(xué)教學(xué)中，適當利用生活資源補充教學(xué)內(nèi)容.在此基礎(chǔ)上，教師不妨收集和應(yīng)用生活中的數(shù)形結(jié)合資源，創(chuàng)新數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用.

比如，在三年級上冊“長方形和正方形”這一課，教師首先向?qū)W生展示生活中的長方形和正方形，引導(dǎo)其對這些圖形展開觀察和討論.基于生活經(jīng)驗，許多學(xué)生已經(jīng)熟悉長方形和正方形事物，進而給予教師“這個旗幟是長方形”“這個塑料板是正方形”等反饋.教師可在此基礎(chǔ)上提問，指導(dǎo)學(xué)生遷移生活經(jīng)驗，在圖形實物中提煉幾何特征：“比較生活中的長方形和正方形，嘗試畫一畫它們的簡圖，說說長方形和正方形有什么特點.”提出問題后，教師可以向?qū)W生發(fā)放不同的實物道具.按照問題要求，學(xué)生參照實物道具畫圖，有的直接在道具上覆蓋白紙、描圖，有的先用直尺測量道具每條邊的長度，再將相同長度的線條畫在白紙上，使其構(gòu)成封閉圖形.此時，數(shù)形結(jié)合思想被第一次應(yīng)用，即生活圖形（數(shù)學(xué)的生活形態(tài)）與數(shù)學(xué)圖形（數(shù)學(xué)的本質(zhì)形態(tài)）有機結(jié)合，學(xué)生在生活圖形中抽象出數(shù)學(xué)圖形，識得長方形和正方形.

其次，教師要肯定學(xué)生的畫圖學(xué)習(xí)過程，并提問學(xué)生：“通過剛才的測量和畫圖，你們有哪些發(fā)現(xiàn)？”學(xué)生回憶測量結(jié)果，給予教師“長方形和正方形都有四條邊”“長方形其中兩條對著的邊比另外兩條對著的邊要長”“正方形的四條邊都一樣長”等反饋.此時，數(shù)形結(jié)合思想被第二次應(yīng)用，學(xué)生在“長度”的數(shù)量關(guān)系支持下增進圖形認知，理解長方形和正方形的邊長或長寬特征.教師可以趁熱打鐵，提出“畫一個長為6厘米、寬為4厘米的長方形”“畫一個邊長為5厘米的正方形”等畫圖要求，指導(dǎo)學(xué)生仿照剛才的圖形畫出固定邊長的長方形或正方形，使其進一步理解邊長對圖形的影響.

最后，教師指導(dǎo)學(xué)生關(guān)注長方形和正方形角的大小.比如，教師引導(dǎo)學(xué)生通過三角板和量角器測量長方形和正方形的角.通過測量，學(xué)生能夠發(fā)現(xiàn)：無論是生活形態(tài)的長方形和正方形，還是數(shù)學(xué)形態(tài)的長方形和正方形，它們的四個角都是90°.此時，數(shù)形結(jié)合思想被第三次應(yīng)用，學(xué)生從不同角度切入，認識長方形和正方形的角，完善圖形認知：（1）長方形和正方形都有四條邊和四個角.（2）長方形的對邊相等，長一點的對邊是長方形的長，短一點的對邊是長方形的寬；正方形四條邊都相等.（3）長方形和正方形的角都是直角.

至此，生活化數(shù)形結(jié)合資源充分促進了數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用，讓學(xué)生在生活中樂學(xué)、善學(xué).

（三）規(guī)劃教學(xué)，把握數(shù)形結(jié)合時機

教師不能將數(shù)形結(jié)合思想“一股腦”地應(yīng)用在小學(xué)數(shù)學(xué)教學(xué)中.結(jié)合現(xiàn)有研究與實踐結(jié)果來看，數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的最佳應(yīng)用時機，應(yīng)包括學(xué)生建立概念時、理解和解決問題時.故而教師應(yīng)規(guī)劃教學(xué)，把握數(shù)形結(jié)合時機，使數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用具有一定計劃性.下面重點圍繞“概念”與“問題”，分析數(shù)形結(jié)合策略.

1.在建立概念時應(yīng)用數(shù)形結(jié)合思想

概念是“教數(shù)學(xué)”的起點，也是“學(xué)數(shù)學(xué)”的基礎(chǔ).小學(xué)數(shù)學(xué)教學(xué)中，教師應(yīng)使學(xué)生充分理解每一個概念，建立完整的概念系統(tǒng).而在一些抽象概念中，學(xué)生較難實現(xiàn)此目標.教師可基于此應(yīng)用數(shù)形結(jié)合思想，借助“數(shù)”與“形”的相互轉(zhuǎn)化，消除學(xué)生的概念困惑.

（1）構(gòu)建直觀圖，建立“數(shù)”的概念

以“形”化“數(shù)”，有利于學(xué)生建立“數(shù)”的抽象概念.教師可基于“數(shù)”的特征指導(dǎo)學(xué)生構(gòu)建直觀圖，進而通過圖形幾何意義促進學(xué)生建立“數(shù)”的概念.

例如三年級上冊“分數(shù)的初步認識”這一課，部分教師在教學(xué)中直接講解概念“把一個物體平均分成幾份，其中的一份就是這個物體的幾分之一，其中的幾份就是這個物體的幾分之幾”，學(xué)生沒有經(jīng)歷“平均分”“份數(shù)”“幾份”的構(gòu)建過程，很難建立清晰的“分數(shù)”概念.教師可構(gòu)建“涂色”等直觀圖，在“形中有數(shù)”中實現(xiàn)數(shù)形結(jié)合思想的有效應(yīng)用，促使學(xué)生建立“數(shù)”的抽象概念.比如，教師通過課件出示圖1：

（2）基于“數(shù)”的轉(zhuǎn)化，建立圖形概念

以“數(shù)”化“形”，有利于學(xué)生建立“形”的抽象概念.教師可基于圖形與“數(shù)”的規(guī)律，指導(dǎo)學(xué)生用“數(shù)”描述圖形，進而使學(xué)生成功建立圖形概念.

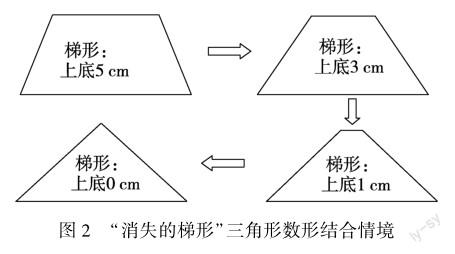
例如四年級下冊“三角形”這一課，三角形可以被視為上底為0的梯形.教師可在教學(xué)中，通過圖2創(chuàng)設(shè)“消失的梯形”情境.課件中，梯形下底長度不變，上底長度不斷變小，直到變成0.學(xué)生觀察課件動畫，得到“梯形上底長度為0時，就變成了三角形”的結(jié)論，能夠在“數(shù)”的變化中，發(fā)現(xiàn)認識三角形的新角度，同時建立三角形的正確概念.

之后講解等腰三角形、等邊三角形時，教師同樣可運用此方法.比如在講解等邊三角形時，教師可先通過課件出示一個普通三角形，再以某一條邊為基準，緩慢改變另外兩條邊的長度，直到三條邊的長度完全相等.通過直觀感受三角形其中三條邊由“長度不同”到“長度相同”的變化，并且用“數(shù)”的語言描述變化的具體內(nèi)容，學(xué)生可準確建立“等邊”概念，確定什么是等邊三角形.

2.在理解問題和解決問題時應(yīng)用數(shù)形結(jié)合思想

理解問題是解決問題的前提，而在當前小學(xué)數(shù)學(xué)教學(xué)中，經(jīng)常出現(xiàn)學(xué)生不能準確理解問題的情況，以至于學(xué)生不能正確解決問題.歸根結(jié)底是因為部分問題過于抽象，學(xué)生不能通過閱讀全面判斷其內(nèi)容.教師可以示范“畫圖解題法”，帶領(lǐng)學(xué)生將抽象“數(shù)”的語言轉(zhuǎn)化為直觀的“形”的語言，在加速學(xué)生理解問題的同時，培養(yǎng)學(xué)生數(shù)形結(jié)合讀題習(xí)慣，提高學(xué)生的解決問題能力.

問題要素較多，數(shù)量關(guān)系也相對復(fù)雜，不利于學(xué)生理解和解決問題.教師可示范“線段圖”，如圖3.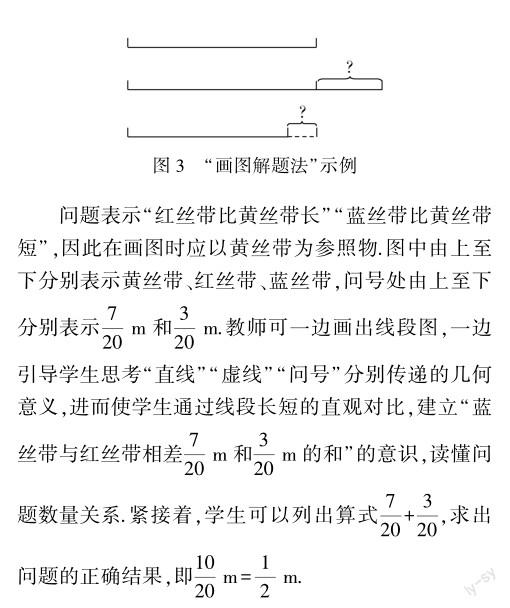

在學(xué)生熟練此理解和解決問題的策略后，教師還可以設(shè)計拓展問題，將畫圖主動權(quán)全部交給學(xué)生，使其完整經(jīng)歷畫圖解題過程.

結(jié) 語

總之，觀察性原則與操作性原則，是數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用原則，教師應(yīng)基于“看圖”與“畫圖”，逐漸引導(dǎo)學(xué)生形成數(shù)形結(jié)合思想.在此基礎(chǔ)上，教材與生活中均充斥著數(shù)形結(jié)合元素，學(xué)生應(yīng)將數(shù)形結(jié)合思想充分滲透在建立概念、理解和解決問題方面.教師應(yīng)挖掘和整理教材數(shù)形結(jié)合元素，收集和應(yīng)用生活中的數(shù)形結(jié)合資源，規(guī)劃實際教學(xué)中的數(shù)形結(jié)合時機，以此讓數(shù)形結(jié)合思想全面賦能于實際教學(xué)，引領(lǐng)學(xué)生循序漸進發(fā)展.

【參考文獻】

[1]戚海燕.“數(shù)形結(jié)合”思想在小學(xué)數(shù)學(xué)教學(xué)中的靈活應(yīng)用[J].智力，2022（34）：60-63.

[2]張鵬華.數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的滲透與應(yīng)用[J].讀寫算，2022（33）：54-56.

[3]相輝.重視顯示形象 促進深度學(xué)習(xí)———“數(shù)形結(jié)合”思想在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用分析[J].小學(xué)教學(xué)設(shè)計，2022（32）：4-6.

[4]阮玉芬.“數(shù)形結(jié)合”模式在小學(xué)數(shù)學(xué)教學(xué)中的有效應(yīng)用[J].小學(xué)生（中旬刊），2022（4）：19-20.

[5]凌建軍.數(shù)形結(jié)合思想在小學(xué)數(shù)學(xué)教學(xué)中的滲透與應(yīng)用[J].安徽教育科研，2022（8）：58-59.