高中數學探究活動課“圓的切線與切點弦”教學設計

編者按：課堂是教學的主陣地。優秀的教學設計能為教師提供經驗與啟示，幫助教師提高教學質量。為此，2024年，本刊開設專欄《典型課例》。在該欄目中，我們以“教學設計+點評”的形式，呈現一線教師學習、理解新課標，深化素養導向的課堂教學改革和育人方式轉變的實踐與思考。我們主要呈現2023年江蘇省優質課評比一等獎的教學設計，希望通過這些典型課例，引領教師關注教學細節，激發教學靈感，在實踐中探索、總結和創新，不斷提升教學質量。

【關鍵詞】高中數學；數學探究；教學設計；圓的切線與切點弦

【中圖分類號】G633.6 ?【文獻標志碼】A ?【文章編號】1005-6009（2024）03-0043-04

【作者簡介】劉銀，江蘇省鎮江第一中學（江蘇鎮江，212016）教師，數學學科中心教研組長，高級教師，鎮江市數學學科帶頭人。

一、教學內容分析

《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“新課標”）指出：數學探究活動是圍繞某個具體的數學問題，開展自主探究、合作研究并最終解決問題的過程。［1］這種活動是運用數學知識解決數學問題的綜合實踐活動，是培養學生創新意識和能力的重要途徑。

本節課的內容選自蘇教版《普通高中教科書·數學》（選擇性必修第一冊）第2章《圓與方程》章末“問題與探究”，是本章知識的延伸和拓展，也是后續圓錐曲線相關內容學習的起點和基礎。本節課旨在引導學生運用數形結合、轉化化歸等多種思想方法，深化學生對“代數方法解決幾何問題”的理解和認識。本節課是通過研究點與直線的“對應組”和圓之間的位置關系，讓學生深入體會點在圓上、點在圓外、點在圓內三種情況及三者之間相互遞推的邏輯關聯。在類比聯想、分類整合等過程中，讓學生體會數學的簡潔、統一、和諧、理性之美。

二、教學目標設置

1.經歷直觀想象、畫圖試驗、觀察類比、猜想驗證等探究過程，掌握過圓上一點的圓的切線方程的證明方法。

2.體會探究解析幾何問題的基本方法，發現點不在圓上時方程“x0x + y0y = r2”的幾何意義。

3.在發現問題、提出問題、分析問題、解決問題、再發現新問題的螺旋式上升的探究過程中，激發學生數學探究的興趣與意識，積累活動經驗，培育創新精神。

三、學情分析

1.學生已有的認知基礎

本節課的授課對象是江蘇省四星級高中高二學生，他們能從代數角度研究點、直線、圓之間的關系，初步具備研究解析幾何的直接經驗，具有一定的圖形識別、問題發現以及探究推理能力。

2.達成目標所需的認知基礎

圓的切線與切點弦中，點、線、圓的關系復雜且深刻，數形轉化與融合程度要求較高，需要學生有良好的直觀想象、邏輯推理能力和獨立思考、合作交流等學習習慣。

四、教學過程設計

1.單元回顧，升華認識

師：數學用“符號”將世界抽象為形與數。前面我們學習了“圓與方程”，其中圓是“形”，方程是“數”。

【問題1】在《圓與方程》這一章我們研究過哪些知識？

【設計意圖】通過問題，教師引導學生自主回顧單元知識，這一章主要研究了圓的代數表示以及點、線、圓的位置關系，引領學生進一步升華認識：單個圖形主要研究它的方程及自身的結構特征；組合圖形主要研究它們的位置關系。這為后續研究圓的切線與切點弦及獲得探究路徑作鋪墊。

2.溫故知新，方法引領

【問題2】已知點P（x0，y0）是圓O：x2 + y2 = r2上一點，請畫出過點P的圓O的切線，并求切線方程。

學生活動：由于直線與圓相切，且P為切點，觀察到切線與OP垂直，先求直線OP的斜率，再根據斜率乘積為-1，得切線斜率，進而利用點斜式表示直線，但要單獨考慮斜率不存在或者為0的情形；同樣通過垂直，設切線上任意一點Q（x，y），借助向量，有[OP]·[OQ] = r 2，整理得解；觀察到圓心到切線的距離等于半徑，設直線方程，利用點到直線距離公式求解；觀察切線與圓有唯一公共點，聯立方程，根據方程根的判別式求解。

【設計意圖】問題2是教材習題原題，求解方法較多，有代數、幾何、向量三個視角，但總體來看都是在“形”上抓“垂直”。通過本題的探究，教師帶領學生回顧求解方法和圖形觀察角度，助推學生總結直線與點、直線與圓位置關系的判斷方法，引領后續探究。

【問題2.1】對于向量數量積與方程x0x0 + y0y0 = r2的結構上的聯系，你還有新發現嗎？

【問題2.2】從“數”的角度看，點、線、圓三者之間又有什么聯系？

從“形”的角度看，P點在圓上，從“數”的角度方程上有x02 + y02 = r2，則點的坐標（x0，y0）滿足方程x0x + y0y = r2。學生猜想：此直線是切線；事實上，可以進一步驗證d = [r2x20+y20] = r，因此方程確實表示圓的切線。由此得到命題1。

命題1：當點P（x0，y0）在圓O：x2 + y2 = r2上時，方程x0x + y0y = r2表示圓的切線。

【設計意圖】從數到形，以形助數，幫助學生獲得方程背后的幾何意義。上述探究過程緊扣教材，并將數學思想方法在課堂中落實。在分析解決問題的過程中，為后面“點不在圓上”情況的探究作鋪墊，積累探究經驗。

3.合作探究，形成路徑

【問題3】數學家波利亞曾說：“解題就像采蘑菇，當我們發現一個蘑菇時，它的周圍可能還有其他蘑菇。”你還想探究什么問題呢？

【設計意圖】從點在圓上到點不在圓上，即從點的坐標滿足圓的方程，到點的坐標不滿足圓的方程，進而探究點在圓外和點在圓內。這里從相等到不等，從特殊到一般，引出課題，同時滲透了數學思想方法和數學文化。

【問題3.1】當點P（x0，y0）在圓外時，方程x0x+y0y=r2表示怎樣的直線？

【問題3.2】你能在練習紙上畫出這條直線嗎？

【問題3.3】如圖1，你能判斷直線x0x + y0y = r2與點P（x0，y0），與圓x2 + y2 = r2的位置關系嗎？如何判斷？

【設計意圖】通過問題鏈的方式，教師引導學生根據“點在圓上”的探究方法，交流、討論，通過合作探究解決新問題。

教師補充定義：切點弦是一條特殊的弦，是過圓外一點引圓的兩條切線連接兩切點得到的。

學生活動：

（代數法）記直線與圓交于A，B兩點，與OP交于點H，連接OA，OB，PA，PB。首先由直線斜率可判斷OP與AB垂直，其次計算圓心到直線距離d=[r2x20+y20]，其中OP=[x20+y20]，所以OH·OP=r2，即OH·OP=OA2，所以△OAH ∽△OPA，則OA⊥PA。OA是半徑，所以PA是切線，同理，PB是切線，方程x0x+y0y=r2表示切點弦。正向證明，由數想形，方程表示兩切點所在直線。

（幾何法）過點P作圓的切線PA，PB，則PA⊥OA，PB⊥OB，借助幾何關系，有O，A，P，B在以OP為直徑的圓上。該圓方程為x2 + y2 - x0x - y0y=0，AB為兩圓相交弦，將兩圓作差即可。這里的公共弦就是切點弦，與該直線方程x0x + y0y = r2一致。

（向量法）過點P作圓的切線PA，PB，記OP與AB的交點為H，設直線AB上任意一點，則通過向量知識有[OP]·[OQ] = OH·OP，此時OH·OP = r2，所以[OP]·[OQ] = r 2，即得直線方程x0x+y0y = r2。

【問題3.4】利用剛剛所得的“切線結論”（命題1），能推導出切點弦所在的直線方程嗎？

學生活動：設A（x1，y1），B（x2，y2），切線PA的方程為x1x + y1y = r2，切線PB的方程為x2x + y2y = r2。它們均過點P，有x1x0 + y1y0 = r2，x2x0 + y2y0 = r2。x1x0 + y1y0 = r2與x2x0 + y2y0 = r2結構相同，兩點確定一直線，即x0x + y0y = r2就是直線AB的方程。設而不求，將點在圓外化歸到點在圓上，體現了轉化與化歸思想。由此得到命題2。

命題2：當點P（x0，y0）在圓O： x2+y2=r2外時，方程x0x+y0y=r2表示圓的切點弦所在的直線。

【設計意圖】上述教學從數出發，探究方程背后所蘊含的幾何特征，由數想形，以形助數。與“圓的切線”情形一致，仍在形上抓“垂直”，在數上看“結構”，代數、幾何、向量三種視角前后貫通。在猜想與求證中，學生判斷出直線不經過該點、直線與圓相交，逐步精準定位，得出方程x0x + y0y = r2表示切點弦所在的直線。

4.自主探究，形成體系

【問題4】當點P（x0，y0）在圓內時（P異于O），方程x0x + y0y = r2表示怎樣的直線？

學生活動：過P點作直線，與圓O交于A，B兩點，分別過A，B兩點作圓O的切線，設兩切線的交點Q（m，n），則直線AB可表示為xm+yn=r2。點P在AB上，則x0m+y0n=r2，所以Q點的軌跡方程為x0x+y0y=r2。這個過程就是剛剛“切點弦”逆過來，體現了化歸思想。由此得到命題3。

命題3：當點P（x0，y0）在圓O： x2+y2=r2內時，方程x0x+y0y=r2表示圓的弦切線交點的軌跡。

【設計意圖】“點在圓上”師生共研，感悟探究方法；“點在圓外”生生合作，形成探究路徑；“點在圓內”充分發揮學生的主觀能動性，教師從引導者轉變為“旁觀者”、合作者，幫助學生從“學會”到“會學”。

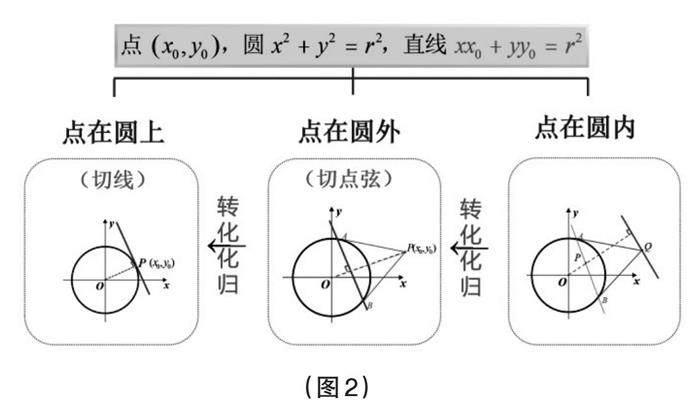
【問題4.1】點在圓上、點在圓外、點在圓內，它們之間有怎樣的聯系？

教師借助GeoGebra軟件動態演示，讓學生從幾何直觀和理性層面體會三種情況下的變與不變。（如圖2）三個問題彼此關聯（直線始終與OP垂直），又層層遞進。過程中，學生感悟到轉化與化歸的數學思想，即“點在圓外”可以轉化到“點在圓上”求解，而“點在圓內”又可以轉化到“點在圓外”求解。教學中，教師還借用了笛卡爾的名言：“我解決過的每一個問題都成為日后用以解決其他問題的法則。”滲透了數學文化。

5.總結回顧，探究繼續

【問題5】請同學們從知識、方法、思想幾方面回顧本節課的收獲。

學生活動：學生結合板書分別從知識、方法、思想等層面總結。知識層面上，點P（x0，y0）在圓O： x2 + y2 = r2上時，直線x0x+y0y=r2表示圓的切線；點P（x0，y0）在圓O： x2 + y2 = r2外時，直線x0x +y0y = r2表示圓的切點弦所在直線；點P（x0，y0）在圓O： x2 + y2 = r2內時直線x0x + y0y = r2表示圓的弦切線交點的軌跡。探究方法上，有類比、聯想、實驗、猜想等。在數學思想上，學生體會了數形結合、特殊到一般、轉化與化歸。探究中借助了代數、幾何、向量三個視角，其中學生特別體會了代數法在解析幾何中的應用魅力。

【設計意圖】引導學生學會尋找研究方法、付諸實踐，學會反思學習過程，提煉研究成果。

6.課后作業，深化鞏固

【思考運用】當“圓心不在原點”時，如何研究圓的切線與切點弦？

【探究拓展】運用今天的研究方法，你還能進行其他探究嗎？

【設計意圖】滿足不同層次學生的需求，將探究意識從課內延伸到課外，激發學生后續的研究興趣，為學生構建“前后一致、邏輯連貫”的學習過程。

【參考文獻】

［1］中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［S］.北京：人民教育出版社，2020：35.

［2］單墫，李善良.普通高中數學教科書·數學（選擇性必修第一冊）［M］.南京：江蘇鳳凰教育出版社，2021：72.