學科記憶育德的實踐路徑*
許天樞 朱加佳

【摘 要】學校教育要突出對學生道德品質與能力素養的培養。課堂教學應以學生的整體發展為目標,實施指向育人的教學實踐。教師在學科教學過程中應充分挖掘學科的育人價值,將學科文化記憶與學生品德培養相結合,發揮學科的育人價值。
【關鍵詞】記憶育德;學科育人;數學課堂;勾股定理
【中圖分類號】G421? 【文獻標志碼】A? 【文章編號】1005-6009(2024)15-0022-04
【作者簡介】1.許天樞,南京市寧海中學分校(南京,210036)校長,高級教師,江蘇省數學特級教師;2.朱加佳,南京市第五十中學(南京,210003)教師,二級教師。
記憶作為客觀事物在人腦海中留存的主觀印象,建構于人對客觀事物理解的基礎上。記憶育德通過調用記憶的方式將已知事物再融合理解,挖掘其中的育德價值,并滲透進學科教學中。以數學學科為例,數學文化是數學學科學習中的獨家記憶,不僅可以增強學生的學科文化素養,還可以激發學生的學習興趣,增強學生的民族自豪感。數學教師在課堂教學中喚醒學生的學科記憶,可以激發學生的探究欲,豐富學生的情感體驗,引導學生深入思考,進而形成正確的世界觀、人生觀和價值觀。
勾股定理作為“千古第一定理”,是數學學科發展的里程碑,從數量關系到位置關系,聯結了代數與幾何。本文以“勾股定理”課堂教學為例,談教師如何引導學生在“勾股定理”的發現與發展歷程中感受數學文化,探索數學學科記憶育德的實踐路徑。
一、尋找記憶:在文化印記中發現數學
教師應在歷史發展的進程與學科文化的傳承中喚醒學生的學科記憶,尋找適配主題的記憶元素,構建記憶場,形成相關的記憶單元,為課堂教學的實施挖掘記憶素材,充分發揮記憶的育德作用。
教學導入階段,教師可以出示圖1,圖2,圖3。圖1分別是2002年在北京舉行的國際數學家大會與2021年在上海舉行的國際數學教育大會的會徽,設計理念源于我國1800多年前三國時期趙爽的《周髀算經注》,該書記錄了對勾股定理最早的證明。圖2為“勾股圓方圖”,這表明勾股定理是我國古人智慧的結晶。圖3為1955年希臘發行的郵票,是畢達哥拉斯發現勾股定理的啟發圖案,故勾股定理在西方也被稱為畢達哥拉斯定理。
圖1國際數學大會會徽中的“趙爽弦圖”“勾股圓方圖”元素,昭示了其歷史地位與重要性,說明中國文化受到了世界的重視。這使學生對本節課的主題研究產生敬畏之心,調動了學生主動學習與探究的積極性。
二、重構記憶:在現象觀察中抽象數學
在尋找記憶過程中,學生形成了抽象的數學感知與數學印象,因此在數學文化中提煉數學問題就成為必然,通過問題思考與問題解決引導學生對現象本質的挖掘則是應然結果。教師可引導學生從現象觀察出發,利用幾何直觀感受,猜想得出勾股定理的結論,培養學生嚴謹的思維品質。
教師要將“尋找記憶”中的數學元素轉化為數學問題,引導學生探究其中關鍵數學元素之間的關系。如畢達哥拉斯受啟發的圖案中,抓住關鍵的數量關系——面積,并將其轉化為方格紙上的探究,便于計算與得出結論。記憶重構中,教師引導學生從文化記憶中抽象出數學模型,充分研究它的數量關系,同時將學科的文化記憶融通形成自身的認知記憶。
例如,將圖形關系探究特殊化為易于計算說理的等腰直角三角形的三邊關系,以求得三邊所作正方形的面積,奠定探究面積關系的研究思路(見圖4);在此基礎上變式,形成一般圖案的關系探究,在三邊關系最為典型的[3、4、5]的直角三角形基礎上開展自主探究(見圖5)。這樣既能引導學生利用面積法探索直角三角形的三邊關系,又能夠強化學生對[3、4、5]數據的感知,實現記憶的強化與深度建構。
三、再現記憶:在操作探究中理解數學
伴隨記憶場域的構建,學生腦海中已經形成多個記憶模塊,但缺少每個記憶模塊之間的聯系鏈條。為了將這些記憶模塊形成整體,教師需要在原記憶的基礎上進一步探究與追尋,讓學生能夠像數學家一樣思考,在知識發現和知識應用中形成閉環。教師可通過記憶再現,增強學生對知識探索的自豪感,引發其對文化傳承與發展的共鳴。
從數學文化現象到數學問題,從數學問題回到數學現象,教師在課堂教學過程中挖掘數學文化中的數學問題,引導學生開展探究活動。如“趙爽弦圖”體現的勾股定理,教師可在幾何關系中推理并證明,引導學生從不同角度思考,探索更多的證明方法。教師通過表格呈現直角三角形三邊的規律,指導學生借助數學工具,如字母表示數、完全平方式等進行論證。例如,教師展示圖6,圖7,圖8。圖6為趙爽弦圖的數學化表示,探究四個全等的直角三角形與兩個正方形之間的面積關系;圖7為畢達哥拉斯證明方法,是類似圖6將四個全等的直角三角形翻了出去,找尋三角形與正方形之間的面積關系證得;圖8為美國總統加菲爾德利用面積法證得,探究兩個全等的直角三角形和一個直角三角形之間的關系。三種證明方法都是文化記憶的再現。
四、創新記憶:在問題解決中應用數學
《義務教育數學課程標準(2022年版)》提出,數學教育承載著立德樹人的根本任務和實施素質教育的功能,其中最重要的一項是發展實踐能力和創新精神,形成和發展核心素養,增強社會責任感,樹立正確的世界觀、人生觀、價值觀。在數學課堂學習中,教師通過記憶喚醒與重構,幫助學生形成對知識的初步理解與應用,但知識習得不是教育的最終目標,教師還要關注學生的情感發展與體驗。
1.在問題中尋證明
經過嚴謹的論證過程與猜想之后,學生已經初步形成對勾股定理的認識與理解,將學科的文化記憶構建成為自己的認知與學科知識記憶。此時,教師可引入其他證明方法,引導學生感受數學知識探索過程的殊途同歸,在數學的變化與創新中感知數學之美。
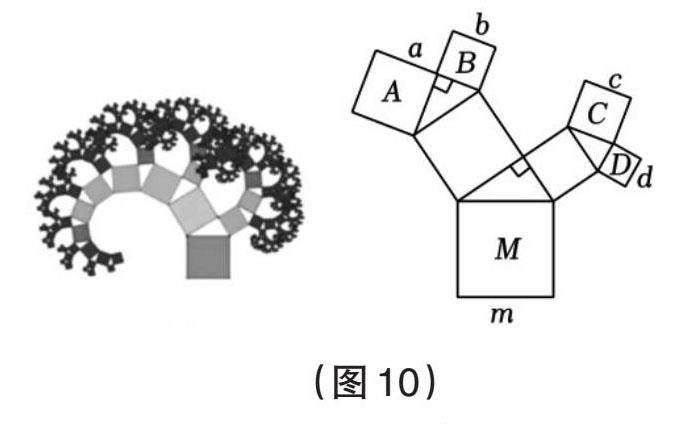
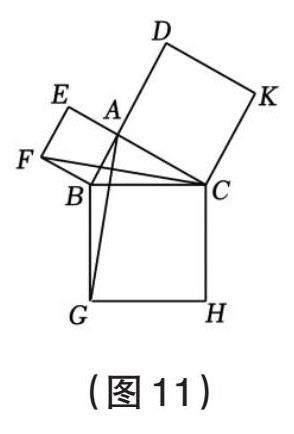
意大利著名畫家達·芬奇證明了勾股定理(見圖9),若設第一幅圖中空白部分的面積為S1,第三幅圖中空白部分的面積為S2,探索S1,S2與a,b,c的關系并利用達·芬奇的方法證明勾股定理。如果以正方形一邊為斜邊向外作直角三角形,再以該直角三角形的兩直角邊分別向外作正方形,重復這一過程后的形狀好似一棵樹,故被稱為“勾股樹”,這是畢達哥拉斯根據勾股定理畫出來的,故被稱為“畢達哥拉斯樹”(見圖10)。在“勾股樹”的某部分圖形中,設大正方形M的邊長為定值m,四個小正方形A,B,C,D的邊長分別為a,b,c,d,探究a,b,c,d,m之間的關系。歐幾里得編纂的《幾何原本》中也有證明勾股定理的方法,教師可借此圖引導學生探究勾股定理(見圖11)。
2.在問題中探應用
從文化到數學、從數學到生活,教師引導學生在解決問題中感受數學文化,以全新的視角思考文化記憶帶動學科發展的過程。例如:教師讓學生觀察“趙爽弦圖”的變化(見圖12)。若將“趙爽弦圖”的四個直角三角形中較長的直角邊分別向外延長一倍,得到如圖所示的“數學風車”,在Rt△ABC中,AC=m,BC=n,∠ACB=90°,求這個風車的外圍周長(圖中實線部分)。教師還可以引入數學文化的問題思考。如圖13,明朝數學家程大位在他的著作《算法統宗》中寫了一首計算秋千繩索長度的詞《西江月》:“平地秋千未起,踏板一尺離地。送行二步恰竿齊,五尺板高離地。”翻譯成現代文為:如圖,秋千OA靜止的時候,踏板離地高一尺(AC=1尺),將它往前推進兩步(EB=10尺),此時踏板升高離地五尺(BD=5尺),求秋千繩索(OA或OB)的長度。
再如,教師可以引導學生探索生活情境問題,這既能提升學生的問題解決能力,又能潛移默化地引導學生形成新的文化記憶理解。如圖14,消防云梯主要是用于高層建筑火災等救援任務,它能讓消防員快速到達高層建筑的火災現場,執行滅火、疏散等救援任務。消防云梯的使用可以大幅提高消防救援的效率,縮短救援時間,降低救援難度和風險。如圖,已知云梯最多只能伸長到50米(即AA'=BB'=50米),消防車高3.4米,救人時云梯伸長至最長,在完成從33.4米(即A'M=33.4米)高的A處救人后,還要從51.4米(即B'M=51.4米)高的B處救人,這時消防車從A處向著火的樓房靠近的距離AB為多少米?
總之,記憶育德建立在學科文化記憶的背景下,通過學科文化記憶的喚醒、重構、創新,促進學生問題解決能力的提升和學科文化素養的發展,充分發揮記憶的德育價值,拓寬了學科德育的途徑。
【參考文獻】
[1] 張大均.教育心理學[M].北京:人民教育出版社, 2011.
[2] 張維忠,唐慧榮.中國古代數學的圖騰:趙爽弦圖[J].中學數學月刊, 2023(6):1-3.
[3] 中華人民共和國教育部.義務教育數學課程標準(2022年版)[S].北京:北京師范大學出版社, 2022.

