在小學高年級數學教學中有效滲透思維培養
盧慧飛


[摘要] 在小學高年級數學教學中,為了促使學生仔細認真、獨立思考、合作交流、反思質疑,教師應當以發散性思維、化歸性思維、綜合性思維為理論支撐,借助圖形與圖形組合、圖形與數字結合、思維導圖展示教學案例,將思維培養滲透于課堂全過程。本文以人教版五年級上冊“組合圖形面積計算”一課為例,探討小學數學教學中有效滲透思維培養的路徑。
[關鍵詞] 教學案例;思維培養;小學數學
為了在數學學習中有效培養小學高年級學生的“獨立思考、合作交流、反思質疑”等學習能力,教師應當根據他們先前掌握的知識與技能,基于發散性思維、化歸性思維、綜合性思維的相關理論支撐,以問題情境導入為突破口,將思維訓練有效融入教學實踐的各個環節。以理論指導實踐,讓思維訓練成為課堂教學主線,有效打破各個教學環節之間的壁壘。基于此,本文以人教版五年級上冊“組合圖形面積計算”教學為例,根據學生先前已經掌握的長方形、正方形、平行四邊形等基本圖形面積的計算公式,依托圖形、數字、思維導圖及其組合的教學案例,有效滲入對學生發散性思維、化歸性思維、綜合性思維等的培養。
一、依托圖形與圖形的組合,促進發散性思維訓練
發散性思維又稱擴散性思維,是對一道問題產生多種分析方法和解決方法,具有創造性思維特點,通常表現為思維角度多樣性和思維視野開闊性,其思維目標分散,思維方向向四面八方擴散。借助發散性思維,學生能從給定的信息中找出新的信息,收獲新的發現,最終更好地解決問題。根據教育心理學的一般定義,發散性思維可以從流暢性、變通性、獨立性三個方面進行表征。具體而言,流暢性是指心智活動靈敏、迅捷,能在短時間內表達更多的內容;變通性是指思維活動能夠隨機應變,觸類旁通,不受某種固定思維模式的局限;獨立性是指以前所未有的新角度觀察事物、分析問題,思維方法新穎獨特,能夠提出新的見解。
上述理論研究充分說明,發散性思維訓練在數學思維培養體系中,應當發揮基礎作用,因為在數學學習中,很多題型呈現出“一題多解”的方式。而且,培養學生的發散性思維,有助于學生更好地理解概念定理,攻克數學學習中的重點、難點。
以人教版五年級上冊“組合圖形面積計算”教學為例,每個組合圖形,往往都是由之前學過的各種具體圖形所組成的。在解題過程中,涉及的計算公式也都是固定的。但是,從不同角度觀察每個組合圖形,其基本構成并不完全一樣。這樣看,發散性思維訓練就在其中發揮著基礎的作用。
如圖1、圖2所示,這是典型的組合圖形面積計算題。通常情況下,教師會引導學生將房子側面圖轉化為“一個三角形+一個正方形”來進行計算。考慮到學生之前已經學過三角形和正方形面積計算公式,所以,他們會很輕松地用“5×5+5×2÷2=30平方米”將房子側面面積計算出來。這樣的解題方法屬于基本解題方法,教師一般要求學生獨立完成這一解題過程,有助于培養廣大學生仔細認真、獨立思考的學習
習慣。
然而,有些教師并不會僅限于以上解題方法的引導,還會組織廣大學生以小組為單位,從不同角度觀察并提問:上述圖2中還有其他哪些具體圖形構成?有的學生回答:“兩個直角梯形。”有的學生會說:“三個三角形。”有的學生認為:“兩個三角形+一個直角梯形。”通過學生的分組發言,最終形成了如圖3所示的八種解題方法:
通過上述“一題八解”的思考過程,學生的思維角度呈現一定的多樣性,思維視野呈現一定的開闊性,這就是發散性思維訓練在思維培養中的有效體現。更為重要的是,這樣的解題方法具有一定的難度,教師安排學生分組觀察與協作,有助于培養他們合作交流的意識與能力。
二、依托圖形與數字的結合,促進化歸性思維訓練
化歸性思維是采用科學方法,根據客觀規律,將問題由疑難轉變為簡易、由繁雜轉變為簡便的一種有效的思維方式。具體到數學學科的學習中,化歸性思維就是將陌生的化為熟悉的、將復雜的化為簡單的、將一般的化為特殊的、將高階的化為低階的、將高次的化為低次的思維方式。換言之,在數學學習中運用化歸性思維,就是將待解決的或者難以解決的問題A經過某種轉化手段,轉化為固定解決模式的或者容易解決的問題B,通過解決問題B來解決問題A。根據這樣的理論定義,說明化歸性思維訓練在數學思維培養體系中,應當發揮不可替代的作用。因為學生在數學問題解答過程中,必然會遇到一些疑難繁雜的題型。作為教師,應引導廣大學生采用合理的解題技巧,將這些疑難繁雜的題型,轉化為簡易、簡便的題型,最終成功解答問題。
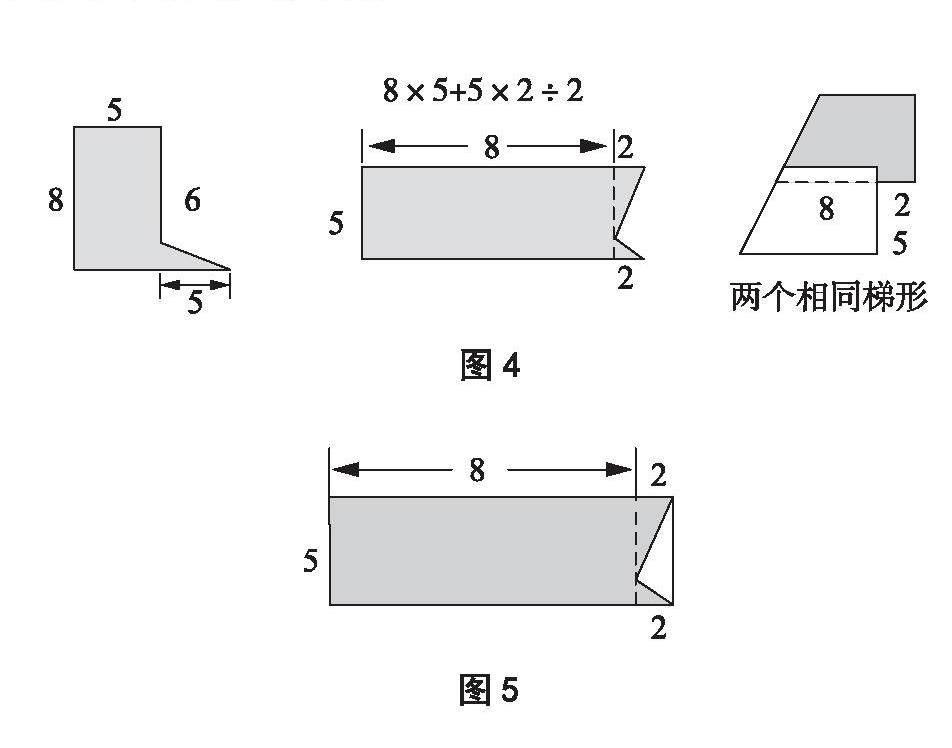
如圖4、圖5所示,在每一種題型的解析過程中,對圖形組合的不同部位進行辨別,只是第一個環節。隨后,學生在教師引導下,需要對不同的長度、寬度、高度、上底、下底進行觀察,并運用相關圖形面積公式,計算出涂顏色部分的面積。
在圖4左側圖形涂顏色的部分中,學生基本上都能認出,它是由“一個長方形+一個三角形”構成的,所以這個圖形涂顏色部分面積很容易就能計算出來。對于圖4中間的圖形,要想計算出涂顏色部分面積,對一些學生來說,確實存在著一定的難度,因為他們往往難以理解:為什么兩個涂顏色的小三角形面積之和是“5×2÷2”?作為教師,應當引導他們明白這樣一個道理:“5×2÷2”既是小長方形面積一半,也是涂顏色的兩個小三角形面積之和(見圖5)。可見,只有將這個道理領悟透徹,才算真正把這道疑難繁雜的題型,轉化為簡易、簡便的題型,才是促進化歸性思維的訓練。
而在圖4右側的圖形中,據調查,20%學生都解答不了涂顏色部分面積,大部分學生想到的轉化方法均不能解答這個題型。為此,在圖6中,教師應組織學生采取獨立思考與分組討論相結合的方式,對這個問題進行解析,教學片段摘錄如下:
學生A:我覺得,①號部分與涂顏色部分的面積
相同。
(其他學生表示不理解)
學生A繼續分析:因為①號+空白部分=梯形,涂顏色部分+空白=梯形,所以①號部分與涂顏色部分的面積相同。然后,我們把①號梯形分成長方形和三角形,長方形(圖中②號)的長是8,寬是5,面積=8×5。這個三角形(圖中③號)的底是2,高等于長方形的寬,也就是5,面積=5×2÷2,將兩部分合起來,列出算式8×5+5×2÷2,算出最后的結果。
教師(在此基礎上)補充:由于兩個直角梯形是相同的,所以①面積+空白部分面積=空白部分面積+涂顏色部分面積,就可以推導出①面積就是所要求的涂顏色部分面積,涂顏色部分面積就是(8+10)×5÷2=45。另一種解題方式是,涂顏色部分面積是由②面積和③面積組成的,②是一個長方形,長度為8,寬度為5,所以②面積為8×5=40,③是一個三角形,底為2,高度為5,所以③面積為2×5÷2=5。最后,涂顏色部分面積就是8×5+2×5÷2=45。
以上兩種方式都能解答涂顏色部分的面積,其中運用到了“等積變換”。因此,讓學生在此項習題中順利掌握“等積變換”的方式方法,就是為了更好地體現化歸性思維的訓練。
三、依托思維導圖的展示,促進綜合性思維訓練
綜合有兩種含義:一是與分析相對,把分析過的對象或現象的各個部分、各個屬性聯合成一個統一的整體;二是不同種類、不同性質的事物組合在一起。綜合性思維是把分析過的對象中的各個部分、各個屬性聯合成一個統一整體。可以說,綜合性思維是多角度、多途徑的想象組合,是超越時空、大范圍、大跨度的想象組合,是思維水平的躍階。在小學高年級的數學學習中,學生所要培養和鍛煉的數學思維其實也是綜合性的,包括前述的發散性思維、化歸性思維,以及幾何思維、抽象思維等,綜合性思維就像一支樂隊的指揮一樣,協調統一著學生已掌握的各種不同的思維模式。
基于這樣的理論定義,綜合性思維訓練在數學思維培養體系中應當發揮支撐作用。因為數學中很多公式,是可以相互轉化的。作為教師,在具體的教學實踐中,需要依托思維導圖,積極引導學生通過對圖形與圖形轉換現象的觀察,將分析過的、零散的計算公式知識點串聯起來,形成一個完整的計算公式知識體系。
例如,在圖7思維導圖教學案例中,可以引導學生思考:“組合圖形面積計算方法與推導出的平面圖形計算方法一樣嗎?并說出其中原因。”通過認真分析,學生意識到:平面圖形與平面圖形之間是可以相互轉化的,沒學過的圖形可以轉化為學過的圖形,陌生的圖形可以轉化為熟悉的圖形;不同圖形的平移、旋轉、軸對稱等知識點具有一定的共通性。以此,將不同的具體圖形整合成統一的圖形,最終發展學生的綜合性思維。
實踐表明,依托思維導圖開展數學教學活動,能有效培養學生的觀察能力與探究能力,所以,教師在此環節中要注重培養學生反思、質疑的思維品質。
總之,在小學高年級數學教學中,教師應以發散性思維、化歸性思維、綜合性思維中的各項理論為支撐,以圖形與圖形組合、圖形與數字結合、思維導圖展示中的教學案例為中心,將思維培養滲透于課堂全過程,努力實現學生數學思維的進階。
[參考文獻]
[1]米山國藏.數學的精神、思想和方法[M].上海:華東師范大學出版社,2019.
[2]谷翠翠,崔瑩.數學文化引領下小學數學單元主題教學新樣態——以“厘米和米的認識”單元教學為例[J].小學數學教育,2021(Z3).
[3]盤艷艷.小學生數學發散性思維培養存在的問題及對策建議[J].教師,2017(30).
[4]王芬.小學數學“發散性思維”培養的研究[J].課程教育研究,2016(21).
[5]崔雪玲,房樹芳.運用化歸思想進行小學數學教學的研究[J].中國多媒體與網絡教學學報(下旬刊),2023(08).
[6]陳俊德.小學數學“圖形與幾何”教學中化歸思想的滲透[J].數學學習與研究,2022(26).
[7]于國勇,李小萍.小學數學練習中綜合思維培養的實踐研究[J].中國多媒體與網絡教學學報(下旬刊),2022(02).

