關注學生探究中數學思維的發展
支新婷

【關鍵詞】數學思維 探究活動 替換
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2014)03A-
0079-02
問題解決策略在蘇教版教材中是一個教學重點。如何將策略教學的思想性滲透其中,把準學生思維的脈搏,突破學生的思維瓶頸,這是教師亟需思考的問題。是為“策略”而策略,還是教會學生解決問題,顯然我們更應注重后者。那么,該如何跳出策略教學的窠臼呢?筆者認為,要關注學生的探究過程,藉以發展學生的思考能力。現以蘇教版六年級上冊《解決問題的策略之替換》為例,談談筆者的體會。
一、創設問題情境,喚醒數學經驗
替換對于學生來說并不陌生,生活中類似的經歷也不鮮見。在課堂中如何讓學生將之前零散的經驗通過數學的方式,整理并形成一種策略,這就需要教師的有效引導。那么,如何喚醒學生的生活體驗呢?
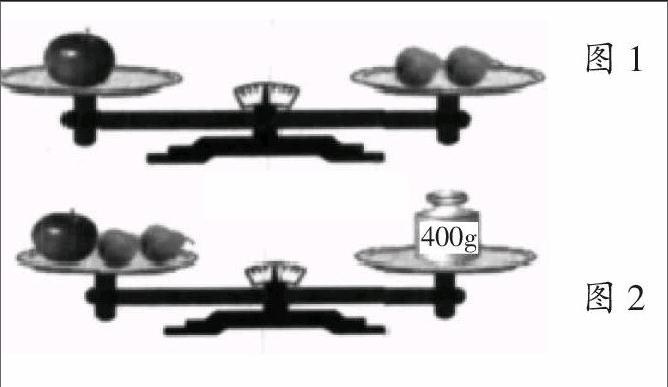
教學中,筆者考慮到要聯系生活實際,從學生耳熟能詳、司空見慣的經歷入手,同時又有數學性滲透,于是選擇了天平來展示,藉此讓學生接觸可感可思的數學素材,搭建數學思維的腳手架。
師:從圖中你能看出有哪些等量關系?
生:一個蘋果和兩個梨是相等的。
師:想想看,你還可以怎么理解?
生:一個蘋果是一個梨的2倍。
生:一個梨是一個蘋果的一半。
師:根據上圖中的兩幅圖,你能知道蘋果和梨的重量分別是多少嗎?說說你是怎么想的。
學生從自己的經驗出發,認為蘋果和梨的總重量是已知的(由天平可知400克),而且蘋果和梨之間的關系也是已知的(蘋果是梨的2倍),因而只要求出其中的蘋果或是梨,另外的就可以得到。現在可以將兩種數量關系變為一種數量關系,即將梨和蘋果進行替換,2個蘋果=400(克),那么一個蘋果等于200(克)。接下來梨的重量就迎刃而解了。
根據學生的辦法,筆者動態演示將蘋果替換為梨或者將梨替換為蘋果,然后進行揭題:這就是我們要學習的替換策略。想想生活中還有哪些替換的例子?(講述曹沖稱象的故事)
在此環節中,筆者使用天平搭建了一個從直觀到感性再到抽象的引渡階梯,激活了學生的自主意識,為下一步自主探究做好了鋪墊。
二、探究解決策略,體驗替換價值
替換策略的重點,是要讓學生理清數量關系,而后建立數量關系間的互相轉化意識。這其中需要滲透數形結合的思想,將復雜的數量關系化為可以直觀感知的數學形式。為此,筆者從例題入手,開展探究活動。
例:丁丁將720毫升的牛奶倒入6個小杯和1個大杯,剛好倒完。小杯的容量是大杯的三分之一,求小杯和大杯各自的容量。
師:題目中小杯是大杯的三分之一,你怎么理解?
生:3個小杯可以換1個大杯。
生:大杯是小杯的3倍。
師:想知道大杯和小杯的容量,能不能直接求出來?
生:不能。需要找到相同的數量關系。
師:用你喜歡的方式,畫出線段圖。
學生的思路是把兩個復雜的數量關系進行梳理:首先將大杯和小杯兩種數量進行合并,變為一種數量,也即大杯(小杯)。而后根據大杯(小杯)的總數量、牛奶的總量來解決問題。根據題目的條件,可將大杯替換為小杯,那么小杯的總數量就是9個,牛奶為720(毫升),由此可知小杯為720÷9=80(毫升);還有一種思路,即將小杯替換為大杯,求出大杯為720÷3=240(毫升)。學生計算之后,筆者引導學生進行如下反思:
1.結果正確嗎?怎么判斷?
2.為什么要將大杯換成小杯(小杯換成大杯)?替換后數量關系有什么變化呢?
根據第一個問題,學生進行檢驗,并體會到要使檢驗符合兩個條件:其一總量要符合720毫升,其二要符合小杯是大杯的三分之一。
針對問題二,學生思考認為:替換策略的價值在于能夠將兩種復雜的量與總量的關系,替換為一種量與總量的關系,使得條件清晰明朗,有利于問題的解決。那么我們根據什么條件來確定替換呢?題目中有一個題眼“小杯的容量是大杯的三分之一”,從題眼可以確定,是否要使用替換策略。在反思和交流中,筆者讓學生從問題本身入手,注重替換策略的運用技巧、使用價值、使用方法等方面的理解,讓學生的數學思維獲得提升。
三、鞏固實踐拓展,發展數學思維
替換教學的本質目標,并非是要學生學會使用替換解決某一道題,而是要通過課堂探究,使其學會明確替換策略的意義和價值,并能夠靈活運用替換策略解決生活中的實際問題。為了鞏固學生對替換策略的認知,加深問題策略的價值挖掘,筆者將問題進行了變式,繼續引導學生探究。
師:如果老師將題目中的條件改為“大杯的容量比小杯多20毫升”,你還可以采用替換來解答嗎?請先用線段圖畫出數量關系。
學生探究討論后發現,如果把大杯替換成小杯,牛奶總量變為(720-20)。那么為什么將小杯換為大杯,牛奶的總量變化了呢?(720+20)
生:原來的例題中小杯和大杯是倍數關系。
生:后來的題中,小杯和大杯的關系是差比。
經過討論后學生明白,不管是倍比還是差比關系,都可以用替換策略,但兩者替換后有一些數量關系發生了改變:前者杯子的總個數變化了,但總量不變;而后者杯子的總個數不變,總量卻變化了。
學生的理性思維從兩種不同的形式中抽象出來后,筆者繼續變式延伸:
如下圖,在右邊的托盤里放兩種水果,可以怎么放?
學生可以有多種選擇:1個蘋果4個梨;1個蘋果1個菠蘿,2個蘋果2個梨等。筆者讓學生根據自己的選擇說一說自己的替換策略,加深理解,使兩個量的替換上升到三個量之間的替換,提高學生的思維能力。
數學是思維的體操,當學生在生活中發現數學的價值,并能夠思考和探究,解決生活中的問題時,那么,開放、靈活的思維將會指引著學生綻放出自主探究、自主發現的花朵,而這正是數學教育帶給學生的美之所在。
(責編 林 劍)

