“三層三環”任務單教學模式在數學課堂中的實踐

陳海女

[摘 要] 自《中小學教師專業標準（試行）》確立“學生為本”的基本教育理念后，“學為中心”為價值取向的數學課堂，倡導將自學、互學、群學三種學習方式有機組合、優化統整. “三層三環”數學課堂利用任務單，通過個體自主學習、小組合作學習、班級展評學習，實現由“教為中心”向“學為中心”的教學模式轉變.

[關鍵詞] “三層三環”；任務單；數學課堂；數學四基

以“學為中心”為價值取向的課堂教學，既是對因材施教思想的弘揚與發展，又是對班級授課制下傳統的以教為中心的集體教學弊端的超越與創新. 有效地將個體自主學習、小組合作學習、班級展評學習三種組織形式有機地結合起來，既有效地促進了學生個性發展、全面發展，更提升了教師教學理念的提升；既體現了自主建構、合作共贏的現代教學理念，又遵循了辯證唯物主義認識論；既培養了學生的獨立精神、合作意識，又兼顧了競爭意識. 一年來，通過實踐，我們在數學課堂中逐步總結和梳理出“三層三環”教學組織形式的邏輯關系和實踐策略.

“三層三環”教學組織形式的邏輯關系

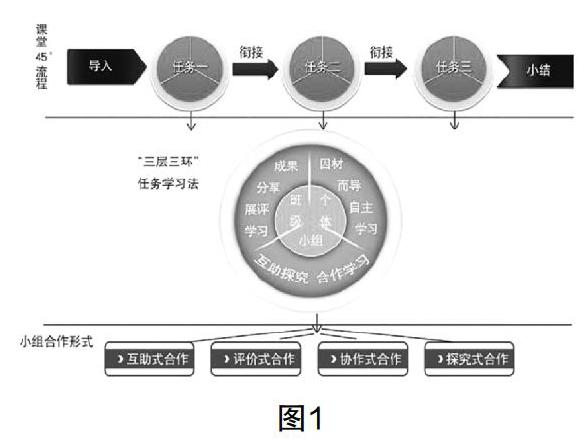
“三層三環”教學組織形式，就其內涵而言，是指在尊重學生個性差異的前提下，為實現一定的教學目標，圍繞教學內容和學習經驗，結合2～3個任務組成的任務單，每個任務從三個層面分別通過三個環節建立起的多向互動課堂教學形式（見圖1）. 其中“三層”是指個體、小組、班級三個學習主體層面，“三環”是指針對每個任務開展的自主學習、合作學習、展評學習三個學習環節.

1.組織形式的互補與遞進關系

“三層三環”課堂組織形式，首先要優化“因學而導”的個體自主學習，注重獨學、自學，這是實施“學為中心”課堂教學的基礎，也是小組合作學習和班級展評學習的前提. 沒有充分的個體自主學習的過程，就不可能有氣氛熱烈的小組合作、學習交流和思維碰撞. 其次要優化“互助探究”的小組合作學習，注重助學、探學. 小組合作學習是生生交流，共享差異的過程. 沒有充分的小組合作學習也就不可能有精彩自信的班級展評學習. 最后要優化“成果分享”的展評學習，注重群學，這是前兩個環節的成果、經驗、思維分享環節，也是學生情感、價值觀目標達成的重要環節. 因此，“三層三環”教學組織形式體現了優勢互補、層層遞進的特征.

2. 任務單對教材的忠實與創生關系

任務單忠實教材與在此基礎上的創生本質是一致的，是源流關系，即任務單源自教材文本. 但“源”并非是“流”，“流”應該是有新質的，即任務單不能脫離課本，否則就成為無源之流了. 因此任務單的設計既要體現教材的基本內容，又要高于教材的理解和把握. 我們在實踐中一般設置2～3個任務，其中一個任務是在教材內容上的拓展、提升. 任務層層遞進，教學組織形式亦是“三層三環”循環推進，這樣的設計也遵循學生的認知發展規律. 同時，并非每個任務都要進行“三層三環”的教學組織形式，當任務比較簡單時，也可以跳過小組合作學習環節，直接進行班級展評學習環節.

3. 師生之間的交往互動關系

教師的教與學生的學是一對相應的命題，本質上是辯證統一的，是教學過程的“一體兩面”，并不存在實質性的矛盾，兩個主體間的交往互動貫穿于三個學習環節. 學生作為學的主體要根據自己的興趣、基礎、能力開展充分的“三層三環”學習，充分發展學生的個體和潛能，要支配更多的時間；教師作為課堂的設計者、組織者、引導者，要協調好教與學的張力. 所謂教師少講，并非削弱教師的作用，而是轉變教師的角色，讓學生真正成為學習的主人. 從整體教學過程來看，教師的作用和工作量不但沒有減少，相反對教師的素養有了更高的要求，尤其是對任務的知識本源、方法本源及思想本源的把握，對課堂的駕馭能力提出了更高的要求.

“三層三環”數學課堂的實踐

一年多的數學課堂教學的實施表明，在“三層三環”教學組織形式下對每個任務一般按照“個體自主學習→小組合作學習→班級展評學習”的過程展開，能很好地達成數學課堂的三維目標，提升數學課堂的有效性.

1. 個體因材而導、自主學習環節

學生在自主、主動、獨立完成任務的過程中，運用學習策略，仔細審題，認真思考，深入分析，解決相關問題. 教師則根據學生的學習起點和教材文本的特點，設計學習任務，提供相應學習資源，并在學生自主學習的過程中進行相應的觀察和個別指導，特別是要結合學生的差異，綜合學生“自學”的時間，為下一環節的學習奠定基礎.

如在《平方差公式》的教學中，出示4個題目，請學生計算：①（1+x）（1-x）；②（2a+3）（2a-3）；③（100-1）（100+1）；④（x-6）（x+3）.

在學生計算初步完成時讓他們思考：（1）各題的結論形式呈現有什么異同？（2）為什么會有這些異同？問題的題干有什么特點？（3）從4個題目的各題干與結果呈現，能分成兩類嗎？你是怎么分的？（4）在計算過程中呈現相同結論形式的各小題有什么規律？

學生對平方差公式的認識，不是追求一開始的誰學得好、學得快，而是強調學習過程的充實感，強調學習對平方差公式生成的體驗，同時不斷積累學習經驗、思維經驗，以及不同學生所產生的多樣化、個體化的思考.

2. 小組互助探究、合作學習環節

小組互助探究、合作學習環節是在個體自主學習完成后，以5～6人的小組為單位的交流活動. 各組在小組長的統一組織下，可以將學習成果進行思想交流，也可以對自主學習解決問題的方法進行互助、探討. 小組學習的有效展開，通過互助、幫扶、協商、合作、探究，可以使學生在小組合作中潛移默化地促進團隊意識、社會性的發展. 根據任務的目標指向的不同，結合數學“四基”，我們總結和構建了4類小組合作的形式：互助式小組合作、糾錯式（評價式）小組合作、協作式小組合作、探究式小組合作.

（1）針對基礎知識的理解，采用互助式小組合作.

根據每個學生的個體差異，針對基礎知識，同一個問題，不同學生對任務理解的程度，分析、解決問題的方法、思路存在多樣性、層次性，這就需要關注學生學習基礎和學習能力的差異，為更好地利用學生的差異，以優助差，助差提優，促進學生對任務的整體解決，我們采用互助式小組合作.

仍以上面《平方差公式》的教學為例，教師在學生自主學習的基礎上，可以組織進行交流，比較4個計算題的答案，統一正確的解題思路，匯報平方差公式的特征、結果呈現. 潛質生提出對于不明白的地方的困惑，組內校對并理解問題、展開分析，達到組內成員澄清認識、理清思路，獲得對問題的全面認識與理解. 若組內仍不明確，則可提交到班級.

（2）針對基本技能的掌握，采用糾錯式小組合作.

數學課程核心理念中提出：人人都能獲得必需的數學. 數學基本技能的掌握就是一種重要的體現. 在鞏固學生對數學計算、運算、演繹、推理、變式時，運用糾錯式小組合作，有較強的針對性、操作性、實用性.

如在學習《一元二次方程》后，出示以下4個題目： ①3x2-4x-1=0；②4x2-8x+1=0；③3（x-2）2=x（x-2）；④（x-2）·（x+1）=9.

首先讓學生自主獨立完成，教師在巡視、觀察中挑選一位優秀的學生進行解答，并在實物投影儀中對解答過程、呈現答案、書寫格式進行榜樣展示. 之后，布置小組糾錯式合作任務：各組檢查組內每一位同學每一個題目的解題情況：①有沒有錯誤？②錯在哪里？③為什么會錯？④怎么改正？⑤還有沒有其他解法？糾錯式合作利用呈現錯誤資源，充分暴露和挖掘學生技能、思維缺陷，并及時有針對性地在組內進行糾正，使學生解一元二次方程的能力得到實質性的提升.

3. 針對基本活動經驗的積累，采用協作式小組合作

很多涉及基本數學活動經驗的任務一個人無法獨立完成，往往需要分解成幾個不同的小任務，由小組合作共同完成，組內每個學生承擔其中的一部分，在分工合作后予以匯總. 任務分解是對問題的深入剖析和解讀，任務分工是對人員、資源優勢的考量，任務執行是答案生成的過程體驗，結論匯總是對任務的整合梳理. 整個學習過程組內成員分工協作，全程參與，能促進學生分析、統籌、探究、合作能力的發展，促進過程性目標的達成.

如在《等可能事件的概率》的教學中，設計了以下兩個活動.

活動1：組織學生進行拋硬幣的游戲，統計有哪些結果，每種結果出現的可能性是否相等.

活動2：組織學生完成擲骰子游戲，回答向上一面點數有幾種不同的結果，每種結果出現的可能性是否相等.

在學生試驗后進一步討論兩個試驗的共同特點. 上述活動需要學生實驗、記錄、計算、總結，可以在2人一組的基礎上，再在組內進行匯總，從而在實驗次數不斷增加的同時，進一步證實結論的可信度.

4. 針對基本思想方法的提煉，采用探究式小組合作

數學是思維的體操，數學課堂應有一定的思維性，數學基本思想和方法應在課堂中有充分的體現. 在個體自主學習的基礎上，學習對任務的多元理解以及多樣化的方法策略. 有些任務難度較大，涉及分類思想、轉化思想等，這些情況需要通過組內交流，共同探究.

如在《二次函數的性質》教學中出示：已知二次函數y=ax2+bx+c的圖像經過（1，0），（-5，0）兩點，頂點縱坐標為，求這個二次函數的解析式. 教師布置任務：你會利用哪些表達式解決問題？學生在個體自主學習后，開展合作學習，分享獨立學習的成果，同時針對不同的解法，小組進行討論，三種函數表達式所對應的解題策略，提升組內同學對任務的認識和理解.

又如任務：已知關于x的方程mx2-（3m+2）x+2m+2=0 ，①求證：無論m取任何實數，方程恒有實數根；②若關于x的二次函數mx2-（3m+2）x+2m+2=0的圖像與x軸兩交點的橫坐標均為正整數，且m為整數，求拋物線的解析式. 分類思想的討論、探究成為了小組合作的方向.

“四基”是數學學習活動的核心內容和主要目標，也是學生數學素養最為重要的組成部分，它們共同構筑了學生的數學知識結構. 合作學習環節與數學“四基”的結合，不是一種合作方式對應“一基”，而是一個任務往往指向多個數學基礎甚至數學“四基”. 只是教師要根據學生學習目標的側重，對應選擇合理的合作方式，指向“一基”的同時，又能兼顧或滲透其他數學基礎. 如上述前三種合作方式，都要對基本數學思想進行滲透.

班級成果分享，展評學習環節

學生在經歷個體因材而導、自主學習和小組互助探究、合作學習環節之后對任務已經有相應的學習成果，教師引導各組（個體）在班級展示取得的成果，引導學生在分享其他組（其他同學）成果的同時，補充本組的不同見解，或對展示的成果進行評價和疑義. 教師結合學生展示與評價，有效介入，順學而導，挖掘數學本源，深化學習成果. 本環節既是任務的知識目標、過程目標達成環節，更是學生語言表達能力、答辯能力、應變能力、社會交往能力及自信心培養的重要環節.

如在上述糾錯式小組合作后，各組代表在班級展示本組在解一元二次方程中出現的錯誤，相互進行補充，利用錯誤資源，針對錯誤進行改正，各組相互進行評價，學生在展示和反饋中加深了對解一元二次方程技能的掌握，在班級分享中構建“雙基”. 又如在幾何教學中，通過各組不同的演繹推理的方法展示，從一題多解到多解歸一，到解法最優化的產生. 學生對幾何推理的多種方式，在更大范圍內進行了交流，從而提升了學習的效果.

行文至此，心里蕩漾起陣陣漣漪，任務單下的“三層三環”課堂模式，是眾多“學為中心”教學組織形式的一種，“學為中心”的課堂變革決不是一項可有可無的教學舉措，而是一場勢在必行且大有可為的革新. 但愿同行們在這場革新中創造出更多、更好的良方，使我們的數學教學實現師生雙贏.