設(shè)計(jì)多層多樣 實(shí)施多步多途

俞建華

[摘要]“長(zhǎng)方體表面積應(yīng)用問(wèn)題”的教學(xué)是長(zhǎng)方體教學(xué)的重點(diǎn)和難點(diǎn)。為改變傳統(tǒng)的教學(xué)思路，在教學(xué)中用“微課題”的形式踐行了“設(shè)計(jì)多層多樣、實(shí)施多步多途”的措施，既滲透了數(shù)學(xué)思想方法，又提升了學(xué)生的數(shù)學(xué)思維水平。

[關(guān)鍵詞]多樣;多途;數(shù)學(xué)本質(zhì);思維品質(zhì)

[中圖分類(lèi)號(hào)]

G623.5

[文獻(xiàn)標(biāo)識(shí)碼]A

[文章編號(hào)] 1007-9068（ 2019）35-0019-04

在“立體圖形的綜合復(fù)習(xí)”的結(jié)課階段，我出示了一道關(guān)于飲料罐的擺放數(shù)量及包裝問(wèn)題（如圖1）。

學(xué)生通過(guò)計(jì)算，得出“可以擺放24罐飲料”。于是我追問(wèn)：“如圖2，24罐飲料可以包裝成3x8、4x6、2x12等不同的形式，為什么廠家選擇4x6的包裝形式？請(qǐng)用自己的理解來(lái)說(shuō)明理由。”

很多學(xué)生嘗試列式計(jì)算三種外包裝的表面積。五六分鐘后，只有個(gè)別學(xué)生計(jì)算出了第一種包裝方式的表面積。于是我就表面積的計(jì)算方法給出提示，可是耗費(fèi)了很長(zhǎng)時(shí)間，學(xué)生還是沒(méi)有得出結(jié)論。我開(kāi)始著急了：“由于時(shí)間關(guān)系，老師把這三種包裝材料的計(jì)算方法都呈現(xiàn)在課件上。”就匆匆結(jié)束了……

這個(gè)尷尬的教學(xué)場(chǎng)景讓我不由得回顧自己20多年的課堂教學(xué)，發(fā)現(xiàn)自己在課堂教學(xué)設(shè)計(jì)時(shí)存在著“四個(gè)一”——教學(xué)目標(biāo)統(tǒng)一、學(xué)習(xí)方法單一、過(guò)程體驗(yàn)唯一、評(píng)價(jià)方式劃一，從而導(dǎo)致課堂教學(xué)存在“四個(gè)缺”——新的教學(xué)理念缺位、指導(dǎo)自主學(xué)習(xí)觀念缺少、關(guān)注學(xué)習(xí)過(guò)程體驗(yàn)缺失、引導(dǎo)自我評(píng)價(jià)能力缺乏。

為改變“四個(gè)一”和“四個(gè)缺”現(xiàn)象，我打算采用“微課題”的形式進(jìn)行教學(xué)，下面就是用“四個(gè)多”來(lái)改變“四個(gè)一”和“四個(gè)缺”的具體措施。

【教學(xué)設(shè)計(jì)】長(zhǎng)方體表面積的教學(xué)不能只停留在表面積的列式及套用公式進(jìn)行機(jī)械計(jì)算的層面上，應(yīng)在學(xué)生已有的知識(shí)經(jīng)驗(yàn)以及思維水平上引入新的問(wèn)題，引導(dǎo)學(xué)生運(yùn)用所學(xué)的知識(shí)提升自己的思維能力，優(yōu)化自己的運(yùn)算及解題策略。于是我對(duì)長(zhǎng)方體表面積可以滲透優(yōu)化教學(xué)的問(wèn)題進(jìn)行了歸類(lèi)梳理，并提出了多層遞進(jìn)、多樣顯示的教學(xué)設(shè)想。

一、注意教材基礎(chǔ)練習(xí)，營(yíng)造情緒氛圍

在學(xué)生學(xué)習(xí)了表面積的概念和計(jì)算方法（人教版教材五年級(jí)下冊(cè)）之后，教材編排了一些練習(xí)幫助學(xué)生加以鞏固。我對(duì)長(zhǎng)方體表面積的計(jì)算練習(xí)進(jìn)行了簡(jiǎn)單的梳理：

對(duì)于上述問(wèn)題的教學(xué)，可讓學(xué)生先自主嘗試，然后利用學(xué)生的原始想法展開(kāi)教學(xué)。首先引導(dǎo)學(xué)生觀察自己列出的算式，運(yùn)用乘法分配率一次或多次提取公因數(shù);再引導(dǎo)學(xué)生進(jìn)行空間想象，把多個(gè)面逐步轉(zhuǎn)化成一個(gè)面。這就是常見(jiàn)的形與式的結(jié)合。

二、注重課內(nèi)補(bǔ)充練習(xí)，創(chuàng)造優(yōu)良環(huán)境

在長(zhǎng)方體表面積計(jì)算的教學(xué)中，教師經(jīng)常會(huì)在課堂上補(bǔ)充一些練習(xí)，學(xué)生在課外作業(yè)中也會(huì)經(jīng)常遇到一些典型的問(wèn)題。這些問(wèn)題主要聚焦于包裝材料上，也是可以進(jìn)行優(yōu)化教學(xué)的：

對(duì)于這兩類(lèi)問(wèn)題的教學(xué)，需要學(xué)生把長(zhǎng)方形想象成一個(gè)側(cè)面加兩個(gè)底面，對(duì)學(xué)生的空間想象能力要求比較高。第一類(lèi)問(wèn)題，需要學(xué)生考慮到有幾種不同側(cè)面的圍法;第二類(lèi)問(wèn)題，需要學(xué)生進(jìn)行觀察比較，利用變中抓不變的思維方法進(jìn)行推理，從而簡(jiǎn)化問(wèn)題。

三、重視拓展延伸練習(xí)，促成深切體驗(yàn)

表面積的學(xué)習(xí)是一個(gè)不斷延續(xù)的過(guò)程。到了六年級(jí)，學(xué)生還會(huì)接觸到空心圓柱體、三棱柱等表面積的計(jì)算問(wèn)題。這類(lèi)問(wèn)題，我把它歸類(lèi)為柱體的表面積計(jì)算，對(duì)其也進(jìn)行一些優(yōu)化教學(xué)的嘗試：

這個(gè)是將長(zhǎng)方體表面積問(wèn)題進(jìn)行延伸后的典型問(wèn)題，可運(yùn)用類(lèi)比遷移的教學(xué)策略提煉出柱體的體積與表面積的計(jì)算方法。只要是柱體，在進(jìn)行空間想象時(shí)，都可以引導(dǎo)學(xué)生把它想象成一個(gè)側(cè)面加兩個(gè)底面，在某種程度上起到了“化繁為簡(jiǎn)”的作用。

【實(shí)施措施】

優(yōu)化意識(shí)不是一朝一夕就能建立的，它需要一個(gè)量的積累，以及逐步滲透、層層內(nèi)化的過(guò)程。基于以上的分析和思考，我采用了緩坡度、慢節(jié)奏、細(xì)實(shí)施的教學(xué)方式，分三個(gè)層面、三個(gè)階段開(kāi)展。

一、利用運(yùn)算定律，生成知識(shí)技能

在學(xué)習(xí)了長(zhǎng)方體和正方體表面積的計(jì)算方法之后，我安排了一節(jié)練習(xí)課，重在引導(dǎo)學(xué)生運(yùn)用乘法分配率，通過(guò)空間想象將一些圖形進(jìn)行重組和變化，從而優(yōu)化思考問(wèn)題的過(guò)程。

1.式形結(jié)合，提煉方法

課件出示（五年級(jí)下冊(cè)練習(xí)六第5題（P36））：有一個(gè)用鐵皮制作的長(zhǎng)方體餅干盒，長(zhǎng)lOcm、寬6cm、高12cm。如果圍著它貼一圈商標(biāo)紙（上下面不貼），這張商標(biāo)紙的面積至少要多少平方厘米？請(qǐng)你盡可能用多種方法計(jì)算。

學(xué)生方法（如圖3）：

師：來(lái)觀察這幾種方法，你能看懂嗎？

生1：方法l是用前后兩個(gè)面加上左右兩個(gè)面。

生2：方法2是把4個(gè)面分成相鄰的2組。

生3：方法3是用表面積減2個(gè)底面的面積。

師：你們能理解方法4嗎？

生4：底面周長(zhǎng)乘高。

師：這個(gè)變化過(guò)程可以借助實(shí)物一起來(lái)理解。（將長(zhǎng)方體側(cè)面展開(kāi)，組織學(xué)生從算式和圖形的角度來(lái)觀察方法1、方法2和方法4的不同與聯(lián)系（如圖4））

師：觀察算式后得知，三種方法之間運(yùn)用了乘法分配率，優(yōu)化了運(yùn)算過(guò)程。從圖形的變化來(lái)看，這是從2組相對(duì)面到2組相鄰面到1組側(cè)面的變化。

學(xué)生在算式優(yōu)化以及圖形組合的過(guò)程中，經(jīng)歷了2ah+2bh→2（ah+bh）→2（a+b）h的思考過(guò)程，最后得出求側(cè)面積的計(jì)算方法是底面周長(zhǎng)乘高，即S側(cè)=Ch。

2.圖形重組，化零為整

課件出示（五年級(jí)下冊(cè)（37）頁(yè)練習(xí)六的第9題）：

師：黃色油漆需要涂哪些面？怎么算？

生1：前面和后面，列式為（40x55+40x65+40x40）x2。

師：這三個(gè)面還可以怎么求？仔細(xì)觀察這三個(gè)面有什么共同的特點(diǎn)。

生2：它們都有一條邊相等，可以把它們組合在一起。

師：你能把想法畫(huà)在黑板上嗎？比如像圖6這樣。

在學(xué)生畫(huà)出了示意圖，并列出了計(jì)算方法“（ 65+55+45） x40x2”后，教師組織學(xué)生比較兩種方法之間的變化關(guān)系，學(xué)生很快發(fā)現(xiàn)了隱含其中的乘法分配率，這就為學(xué)生思考問(wèn)題提供了一條新的途徑。

至此，在解決紅色油漆面積的問(wèn)題時(shí)，大部分學(xué)生就不再急著將每個(gè)面求出后再相加，而是先觀察所求的面有沒(méi)有共同的邊。經(jīng)過(guò)討論交流之后，很快就有學(xué)生想出了新的方法：（ 55+40+10+40+25+40+40） x40。

師：你能看懂這位同學(xué)的方法嗎？

生3：通過(guò)乘法分配率把40“拿”出來(lái)。

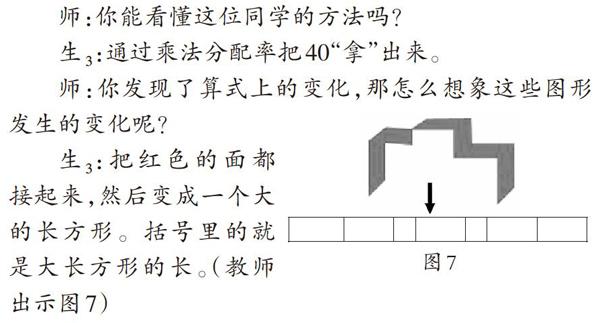
師：你發(fā)現(xiàn)了算式上的變化，那怎么想象這些圖形發(fā)生的變化呢？

生3：把紅色的面都接起來(lái)，然后變成一個(gè)大的長(zhǎng)方形。括號(hào)里的就L是大長(zhǎng)方形的長(zhǎng)。（教師出示圖7）

3.變曲為直，化整為零

課件出示：如圖8，設(shè)計(jì)禮物的包裝紙。請(qǐng)動(dòng)手算一算、畫(huà)一畫(huà)，再判斷這張包裝紙夠嗎？可以怎么包裝？

師：包裝這個(gè)禮物需要考慮幾個(gè)面？

生1：考慮6個(gè)面。

生2：只要考慮3個(gè)面就可以了。

生3：考慮兩個(gè)面，側(cè)面和底面。可以先取一部分包裝紙把禮物的側(cè)面圍起來(lái)，剩下部分再看夠不夠做底面就可以了。

教師組織學(xué)生再次嘗試，但很多學(xué)生都放棄了之前的想法，按生3的想法來(lái)操作。有學(xué)生提出：長(zhǎng)方體的側(cè)面是可以變化的，可以把前后左右或上下前后，或上下左右當(dāng)側(cè)面，所以有多種包裝方法。學(xué)生具體操作后得出兩種方法（圖略）。對(duì)此，教師沒(méi)有直接肯定或是否定，而是引導(dǎo)學(xué)生在解決問(wèn)題的時(shí)候視具體情況而定。

二、巧用通用公式，掌握核心方法

在結(jié)束圓柱體的體積以及表面積計(jì)算學(xué)習(xí)之后，學(xué)生已學(xué)完小學(xué)的立體圖形知識(shí)。教材把長(zhǎng)方體、正方體以及圓柱體的體積公式進(jìn)行了統(tǒng)一，于是，我運(yùn)用類(lèi)比遷移的策略將柱體表面積計(jì)算方法統(tǒng)一，從而優(yōu)化學(xué)生的思維能力。

師：這個(gè)圖形（如圖9）的表面由幾個(gè)面組成？表面積如何算？

生1：5個(gè)面。因?yàn)樗侵w，表面積l為側(cè)面加兩個(gè)底面。

師：你覺(jué)得這里的側(cè)面積可以怎么求？

生2：把三個(gè)長(zhǎng)方形的面積加起來(lái)。

生3：因?yàn)閭?cè)面展開(kāi)是一個(gè)長(zhǎng)方形，所以可以用底面周長(zhǎng)乘高來(lái)計(jì)算。長(zhǎng)方形的長(zhǎng)就是原來(lái)的三角形的周長(zhǎng)，寬就是原來(lái)的高。

生4：結(jié)合算式“3x10+5x10+4x10=（3+5+lO）xl0”來(lái)理解，括號(hào)里是底面的周長(zhǎng)。

學(xué)生在討論交流長(zhǎng)方體、正方體和圓柱的表面積計(jì)算方法的過(guò)程中，結(jié)合三棱柱的表面積計(jì)算方法，歸納得出柱體表面積公式“底面周長(zhǎng)×高+2個(gè)底面積”。

把原來(lái)三維的問(wèn)題看成了二維的問(wèn)題，讓學(xué)生看到柱體就能想到它的表面積是側(cè)面加兩個(gè)底面。將具有共同特征的圖形的相關(guān)計(jì)算方法進(jìn)行統(tǒng)一，不僅降低了對(duì)學(xué)生的計(jì)算要求，還可以發(fā)展學(xué)生的空間觀念，提升學(xué)生的遷移能力。

三、妙用比例思想，培養(yǎng)綜合思維能力

學(xué)完六年的數(shù)學(xué)課程，學(xué)生已經(jīng)掌握了一定的運(yùn)算技能，也具備了優(yōu)化問(wèn)題的意識(shí)，但在一些需要比較的問(wèn)題上，他們還是習(xí)慣計(jì)算后再進(jìn)行比較，比如本文一開(kāi)始就提出的包裝問(wèn)題（如圖2）。對(duì)此，我在復(fù)習(xí)階段就引導(dǎo)學(xué)生用正比例思想去解決類(lèi)似的問(wèn)題，以拓寬學(xué)生研究問(wèn)題的視角，從而優(yōu)化解題策略。

1.出示問(wèn)題，嘗試解題

師（出示圖1和圖2）：這里的省料其實(shí)就是指什么？能用自己的理解說(shuō)明問(wèn)題嗎？（大多數(shù)學(xué)生是用側(cè)面積加兩個(gè)底面積的計(jì)算方法）

2.討論交流，尋求策略

師：有沒(méi)有不是通過(guò)計(jì)算表面積進(jìn)行比較的同學(xué)？

生1：都是24罐，底面是相等的，所以只要比較側(cè)面積就行了。

生2：求側(cè)面積也很麻煩啊。

生3：側(cè)面積可以用底面周長(zhǎng)乘高計(jì)算，既然高相等，只要比較底面周長(zhǎng)就可以了。

生4：只要比較長(zhǎng)與寬的和，因?yàn)橹荛L(zhǎng)等于長(zhǎng)與寬的和乘2，這里的2是不變的。

3.深度討論，直擊本質(zhì)

師：馬上算一算長(zhǎng)與寬的和分別是多少。

生5：4+6，8+3，12+2。

生6：4還得乘5.5，6也要乘5.5 -都要乘5.5再相加。

生7：不用的，大家都乘5.5，都一樣，所以只要比較4+6、8+3、12+2就可以了。

師：對(duì)，可以通過(guò)計(jì)算得出4+6<3+8<2+12，但是它們不是長(zhǎng)與寬的和，而是——

生8：沿著長(zhǎng)邊和寬邊擺放的飲料的數(shù)量和。

學(xué)生通過(guò)討論交流，得出“當(dāng)高相等時(shí)，比較側(cè)面積只要比較底面周長(zhǎng)就可以了”。在這里，學(xué)生運(yùn)用正比例思想，經(jīng)歷了S表一S側(cè)一Cr面周長(zhǎng)一a+b的比較過(guò)程。毋庸置疑，這給學(xué)生提供了一種新的解題策略。

【理論印證】

“設(shè)計(jì)多層多樣、實(shí)施多步多途”的“微課題”印證了以下理論：

1.美國(guó)多樣化和高質(zhì)量研究中心提出的有效教學(xué)的五大原則：第一個(gè)原則是著眼于教學(xué)過(guò)程的質(zhì)量特征，即生成性;第二、第三個(gè)原則是著眼于教學(xué)的基本策略，即交流互動(dòng)和與原來(lái)的經(jīng)驗(yàn)相聯(lián)系;第四、第五個(gè)原則是著眼于教學(xué)的目標(biāo)，即綜合思維能力和語(yǔ)言運(yùn)用能力。這為我的課堂教學(xué)改革提供了可靠的依據(jù)和獨(dú)特的視角。

2.課程標(biāo)準(zhǔn)：有效的學(xué)習(xí)活動(dòng)不能單純地依據(jù)模仿與記憶，動(dòng)手實(shí)踐、自主探究與合作交流是學(xué)習(xí)數(shù)學(xué)的重要方式。

【實(shí)踐感悟】

1.分階段滲透思想方法。主要表現(xiàn)在三個(gè)方面：緩坡度，結(jié)合每一個(gè)新授知識(shí)進(jìn)行提煉，并輔以訓(xùn)練;慢步伐，每次的教學(xué)都放慢步伐，讓學(xué)生對(duì)頭腦中已有的數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)進(jìn)行分析、比較，直至形成比較合理和完善的問(wèn)題解決結(jié)構(gòu);細(xì)實(shí)施，每一階段的教學(xué)，都不排斥原有方法，但必須讓學(xué)生認(rèn)識(shí)到原有方法的局限性，感受新方法的優(yōu)越性。

2.分需求培養(yǎng)思維水平。以學(xué)知識(shí)、長(zhǎng)見(jiàn)識(shí)、悟道理為原則，根據(jù)學(xué)生需求不斷尋找新的方法，凸顯數(shù)學(xué)的本質(zhì)，促使學(xué)生尋求最優(yōu)的策略;致力于學(xué)生數(shù)學(xué)思維的培養(yǎng)，思維品質(zhì)的提升，給學(xué)生帶來(lái)切實(shí)的進(jìn)步和提升。

3.分層次提升自評(píng)能力。不管是運(yùn)用乘法分配率對(duì)算式或者計(jì)算公式進(jìn)行變形，從而進(jìn)行簡(jiǎn)便運(yùn)算，還是利用比例思想轉(zhuǎn)化問(wèn)題，從而簡(jiǎn)化問(wèn)題，都是根據(jù)不同學(xué)生的起點(diǎn)，發(fā)揮其自身的能動(dòng)性，并促其形成自評(píng)的習(xí)慣，從各個(gè)角度肯定學(xué)生的表現(xiàn)與進(jìn)步。

（責(zé)編 金鈴）