建構邏輯連貫的學習拓展數學思維的深度

摘 要:受教學研討活動啟發,仔細解讀教材編寫意圖,建構邏輯連貫的學習過程,使學生在探究勾股定理與圖形面積的關系中,學會有深度的數學思考。
關鍵詞:勾股定理;圖形面積關系;邏輯連貫;數學思維
勾股定理是幾何學中一顆光彩奪目的明珠,被稱為“幾何學的基石”,要把它作為一粒“知識種子”去種植,去啟迪學生的智慧,要發掘它的人文歷史,理順它與圖形面積的關系。筆者為學生搭建前后一致、邏輯連貫的學習過程,使學生在掌握勾股定理與圖形面積關系的過程中學會思考,現整理成文與讀者分享。
一、 研究緣起
筆者有幸參與一次教學研討盛會,深受展示課的設計理念和課堂實踐的啟發,盛會之后從整體上對《勾股定理與圖形面積關系的拓展》進行設計和實踐,以它為知識“源”進行再生長。
(一) 亮點呈現
李老師所授的《勾股定理與圖形面積關系的拓展》,采用“自主探究、合作交流”的教學模式,從注水法實驗展示,到以長三角南京、上海和杭州為頂點構作三角形的形狀判斷,從借助教材內容剪影回顧到張景中院士的無字證明,從神奇勾股樹欣賞到勾股定理與圖形面積關系的拓展,行云流水,一線展開。立足教材起點,從熟悉的基本圖形為切入點,在學生最近發展區里提供一個有探究價值的問題,在探究中點燃學生的思維火花,注重知識、思想的自然生長。
(二) 課堂評價
李老師不管從設計理念,課堂組織,調控駕馭,數學理解,可圈可點之處很多,但總體上學生是被老師牽著鼻子前行,沒有離開老師精心預設的軌道。對《原本》第六卷命題31進行深入學習,隨著時間的推移,學生對命題學習的內容早晚會流失。而教學不僅僅要對事實和技能學習,還有必要使學生揭示隱藏在事實背后的發生發展的歷程,挖掘隱含其中的數學精神、思想和方法等“緘默性知識”。
二、 從邏輯連貫的視角對教學進行設計
《大學》有云:“物有本末,事有始終,知所先后,幾近道矣!”把握教學內容的前后連貫性,幫助學生將零散知識網絡化,促進數學的認識和理解,生長出高階思維的“翅膀”。
(一) 勾股定理為何如此招人“青睞”?
學生已經學習勾股定理,明白它是直角三角形三邊之間的關系,是最著名的定理之一,為什么是最著名的?它在圖形研究、生產實際中有廣泛應用,“廣泛”體現在那些地方?趙爽弦圖為什么能作為在北京召開的第24屆國際數學家大會的會標?為什么有那么多名人去研究勾股定理,對它如此的癡迷?在教學中老師對它為什么如此重視?從課本中獲得一定的認識,但并不是所有的學生會產生上面的質疑和反省。
(二) 幾種版本教材編者都安排“閱讀材料”有何用意?
綜觀幾種不同版本的教材,1. 人教版從畢達哥拉斯對地板花紋的觀察、思考,在格點中計算等腰直角三角形三邊向外作正方形,計算正方形的面積,得到三邊關系,然后從特殊到一般三角形的思考,最后用趙爽弦圖證明。北師大版通過畫圖、測量、數格子、計算等方式得出勾股定理,再對大正方形割補來證明。浙教版從四個全等的直角三角形剪拼引出勾股定理,然后用面積進行證明。編者的意圖大同小異,為什么?2. 人教版在閱讀材料中安排勾股定理多種證法,北師大版在課后的“數學思考”中編排直角三角形三邊上半圓面積之間的關系。浙教版在閱讀材料中介紹勾股定理與面積拓展,以及月牙定理。教材受篇幅限制,不能面面俱到,安排這些閱讀材料有什么用意?想讓學生認識勾股定理從人類生活實際測量面積中來,再回到“形態各異”的圖形面積應用中去,不僅要從思想、方法角度,還要從文化的角度欣賞勾股定理的全貌和魅力,向他們昭示數學是人類文化的重要組成部分。
《易經》云:“取法乎上,僅得其中;取法乎中,僅得其下。”以學生已有的勾股定理知識為出發點,挖掘知識發展的起源,使知識、思想和文化互相貫通。
1. 確定預期的教學結果
(1)了解勾股定理歷史文化,認識勾股定理來源和流向。
(2)探究《原本》第六卷命題31對勾股定理進行面積拓展。
(3)繪制勾股定理的思維導圖,揭示勾股定理與圖形面積之間的關系。
2. 確定合適的評估證據
(1)以任務驅動形式,利用網絡或書籍課前查閱、收集勾股定理的歷史文化知識,并在課堂上請學生對材料進行解釋、闡明、應用、洞察等,體會勾股文化的博大精深。
(2)用動手操作、獨立思考、合作交流和邏輯推理等學習方式,探究《原本》第六卷命題31。
(3)師生一起對所收集的材料進行探討,并繪制思維導圖,理順勾股定理的源與流。
三、 基于邏輯連貫的教學實踐
查閱環節:課前請學生用網絡和書籍,查閱、收集勾股定理有關歷史文獻,備注文獻的來源,遇到疑惑查資料解惑,也可以和身邊的人交流釋疑,并整理成文。(提示:可以從勾股定理來源、命名、證法、推廣和應用等方面收集。)
展示環節:課上請學生先在本小組內交流自己收集的文獻,然后推薦代表展示自己小組內的研究成果,組員協同完成。最后師生對展示成果進行分析、歸納、綜合和概括,對學生存在疑問的地方集體探討。
師:我們已經知道“勾股定理”是世界上最偉大的發現之一,國內外很多人對勾股定理一直保持著極高的熱情。請你們把課前收集的成果按來源、命名、證法、推廣和應用五方面在小組內交流展示,并說明來源。
生1:我們是從命名上收集的,來源于網絡。勾股定理是中文名,在中國古代人們把彎曲成直角的手臂的上半部分稱為“勾”,下半部分稱為“股”,并有“勾三股四玄五”的簡單說法,據說在《周脾算經》最早由商朝時期的商高提出,又名為“商高定理”。在西方最早提出并證明此定理為公元前6世紀古希臘的著名數學家畢達哥拉斯,世界上許多國家都稱勾股定理為“畢達哥拉斯定理”。為慶祝這一定理的發現,畢達哥拉斯學派殺了一百頭牛酬謝供奉神靈,這個定理又叫做“百牛定理”。
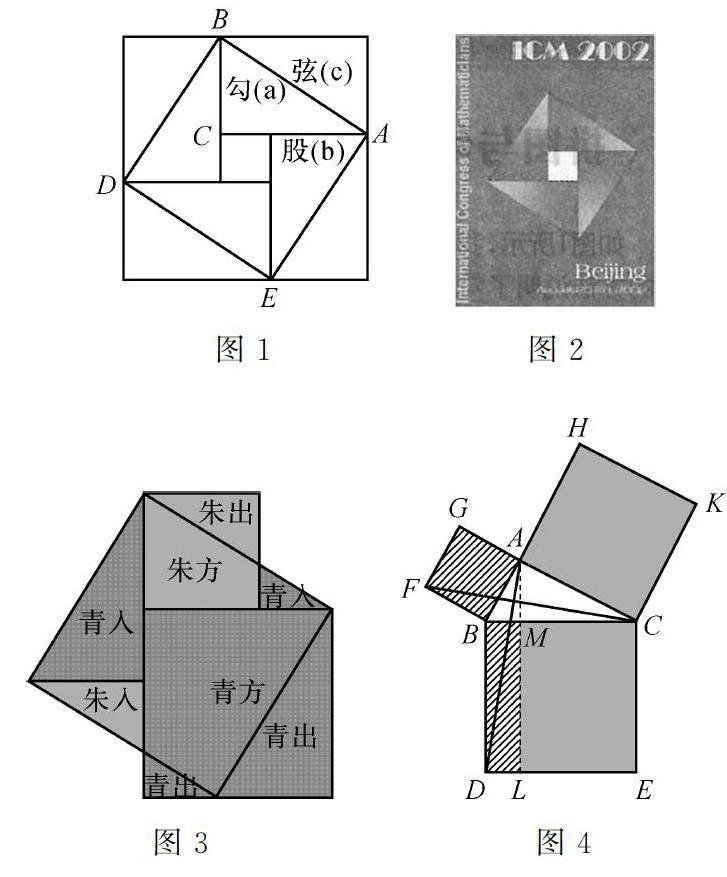
生2:我們從勾股定理的證法上去收集的,來源于書本和網絡。三國時期趙爽為證明勾股定理作“勾股圓方圖”,即“弦圖”,如圖1,前面我們新課中探究過,就不再啰唆。2002年第24屆國際數學家大會在北京召開,中國郵政發行一枚郵資明信片,郵資圖,如圖2就是這次大會的會標中國古代證明勾股定理的趙爽弦圖。
生3:我們組推薦的是古代數學家劉徽用拼出的青朱出入圖,如圖3來證明勾股定理,其大意為:一個任意直角三角形,以勾寬作紅色正方形即朱方,以股長作青色正方形即青方。將朱方、青方兩個正方形對齊底邊排列,再割補——以盈補虛,分割線內不動,線外則“各從其類”,以合成弦的正方形即弦方,弦方開方即為弦長。親愛的同學們,你會證明嗎?鉆研它我沒有少花時間!
生4:在歐幾里得的《幾何原本》一書中給出歐幾里得的證法,設△ABC為一直角三角形,其中A為直角,從A點劃一直線至對邊,使其垂直于對邊,延長此線把對邊上的正方形一分為二,其面積分別與其余兩個正方形相等,如圖4。為了弄明白此證明過程,我在家琢磨好久,很有意思的,其中要用到全等三角形的SAS判定,還要使用面積進行轉化,有興趣的伙伴們可以嘗試。
生5:我們還有美國總統證法,張景中院士的無字證明法,還有看不懂的平面向量法……
師:同學們是否發現,上面的證明方法都是從計算圖形的哪個角度來證明的?
眾生異口同聲:面積。
師:到目前為止,勾股定理的證明方法已有400多種。由于時間關系,在這里就不請同學們一一來展示,有興趣的同學可在你的認知范圍進行思考,整理。除了證明方法外,還有其他嗎?
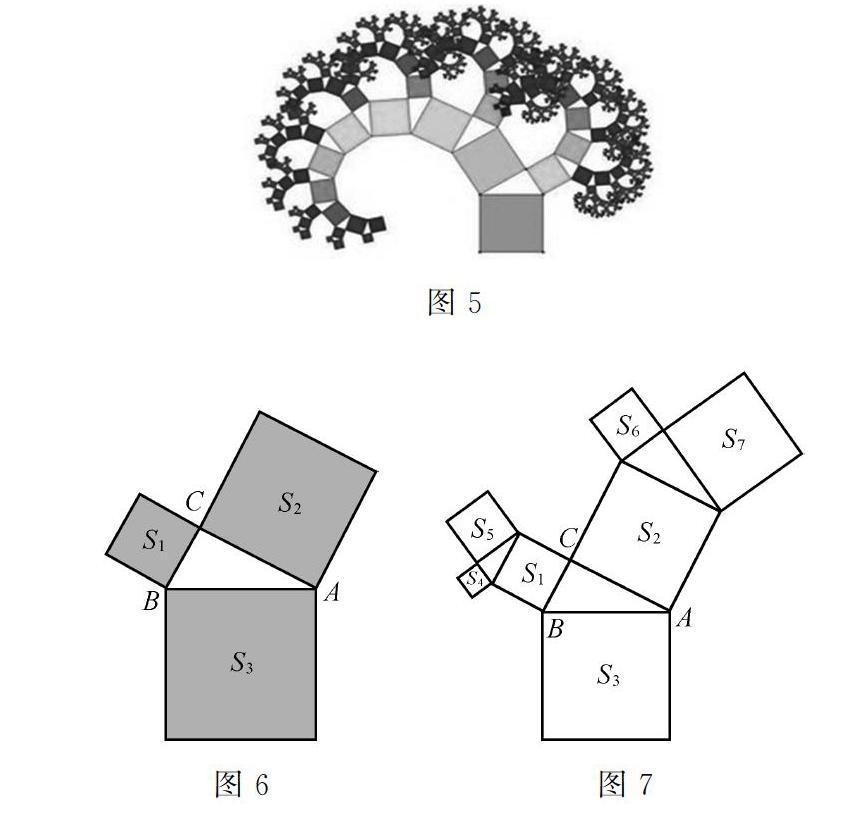
生6:我們從網絡上收集到畢達哥拉斯樹,又叫“勾股樹”,如圖5,是由畢達哥拉斯根據勾股定理所畫出來的一個可以無限重復的樹形圖形,因為重復數次后的形狀好似一棵樹,所以被稱為畢達哥拉斯樹。通過觀察和思考,發現一個很有趣的性質,同一次衍生出所有小正方形面積之和等于最大正方形的面積,你能說出圖6,圖7中,這些圖形面積之間存在的等量關系嗎?
生7:我們在課本的閱讀材料里還發現一個有趣性質:在一個直角三角形中,在斜邊上所畫的任何圖形的面積,等于在兩條直角邊上所畫的與其相似的圖形的面積之和。有點似懂非懂……
點評:利用信息化的便利,學生親身經歷勾股定理相關知識的收集、整理,學會對信息進行過濾,吸收,學會在閱讀中思考,在思考中閱讀,在課堂上進行交流、溝通、合作和解決問題,學會共處,促進多元化發展。其實,人的大腦是個四通八達的交通網絡,每兩個點都被若干條道路連接,有足夠多的道路聯結的地點是核心知識,要以這些知識為“內核”,與其他知識彼此貫通,構成一張知識網絡,勾股定理就是這種核心知識,學生理解它需要經歷知識還原于下層,體驗與探究,反思與上浮的“U型”學習過程,才能獲得知識的意義增值,而不是性質的簡單占有。
探究環節:學生動手操作、獨立思考、合作交流和邏輯推理等方式,探究《原本》第六卷命題31。
師:那我們就一起研究學生7提出的問題。在前面已經知道,分別向直角三角形三邊向外作正方形,圖8中得到結論S1+S2=S3。
師:既然外作正方形有這樣規律,分別以直角三角形的三邊向外任意畫三角形,行嗎?請同學們試試看。(學生畫圖出進行觀察、思考。)
生8:這一結論不一定成立。
師:為什么?談談你的理由。
生8:這三個三角形只是固定了AB,AC,BC的長,而對應邊上的高沒確定,根本沒法計算它們的面積,所以沒法確定S1+S2=S3是否成立。(在黑板上畫出一個圖形9解釋。)
師:反例構造得非常好!這些三角形滿足什么條件結論才能成立呢?請大家試試。(小組進行交流、討論,老師巡視參與小組討論。)
生9:設BC,AC,AB邊上的高為h1,h2,h3,令BC=a,AC=b,AB=c,要使S1+S2=S3成立,只需ah12+bh22=ch32,即有ah1+bh2=ch3,而根據勾股定理有a2+b2=c2,對比這兩個式子,要求h1a=h2b=h3c就可以。
師:對這位同學見解是否有異議?大家試試看。(學生認真地思考,驗證想法,很多同學同意他的想法。)我們想請教剛才提供這么好的想法的同學說說,你是如何發現的?
生9:我主要是對比ah1+bh2=ch3,a2+b2=c2這兩個式子,剛開始只要讓h1=a,h2=b,h3=c這兩個式子一樣,這時大膽的猜想,能否讓h1,h2,h3在a,b,c的基礎上縮小(或者擴大)相同的倍數,即h1a=h2b=h3c=k(k>0),然后代入到a2+b2=c2演算一下,發現是正確的。(該生一邊抓著自己的腦袋,一邊回答說。)
師:這種對比方法太厲害!希望同學們以后多學習他這種大膽猜想的思考方法!上面問題中,我們要求四邊形是正方形,若這三個三角形為……
學生異口同聲說:正三角形。
師:請同學們對這個結論進行驗證試試看。如圖10,分別以Rt△ABC三邊a,b,c為邊向外作正三角形,則S1+S2=S3成立嗎?請說明理由。
生10:老師,正三角形的高線怎么求?
師(面帶狡黠的笑容):獨立思考后發現不會,來尋找幫助很好!由于二次根式的知識還沒學到,推理比較困難,我們可借用幾何畫板進行度量驗證,如圖11,請同學們仔細觀察。(打開幾何畫板,拖動C點觀察三角形面積之間的等量關系。)
圖11
△CAD的面積=10.42厘米2
△CBE的面積=3.45厘米2
△AFB的面積=13.86厘米2
眾生異口同聲:真的相等!
師:上述結論是否適合其他圖形?比方說,向外畫正六邊形是否成立?畫半圓呢?大家試一試!(讓學生進行練習,老師巡視,適當地進行指導。)
師:我們知道正三角形與正三角形、正方形與正方形、正六邊形與正六邊形以及半圓與半圓都是形狀相同的圖形,在九年級學習相似三角形時把它們都稱為相似圖形,通過以上的研究,歸納出性質:在一個直角三角形中,在斜邊上所畫的任何圖形的面積,等于在兩條直角邊上所畫的與其相似的圖形的面積之和。
點評:把課堂真正還給學生,給足學生交流的時空,在交流、對比和思考中體驗勾股定理與圖形面積關系的自然生成。巧妙地將學生置于研究者的狀態,自主地參與到學習活動中來,動手實踐、自主探索與合作交流,這與弗賴登塔爾“再創造原理”有異曲同工之妙,不把數學知識作為預先確定的、正確的東西直接塞給學生,這些東西主要還是靠學生自己的探究和創造來完成,以學生積累的數學活動經驗,數學思考方式來發現問題,提出問題,分析問題和解決問題。
梳理環節:請學生繪制勾股定理與圖形面積關系的思維導圖。
師:前面同學們對展示成果進行交流,收集整理的資料非常詳細,閱讀理解文本非常認真,很會動腦思考!特別是,探究《原本》第六卷命題31對勾股定理進行面積拓展時,思考得十分深入,非常好!其實“勾股文化”豐富多彩,值得我們好好去學習,多多去研究。查閱的資料可歸結為:定理的命名和證明,發展歷程,從形狀和表達式的兩個方面進行推廣,還有應用等。
點評:人的智能核心成分是思維,而概括既是思維的第一特征,也是智能的首要特點。繪制勾股定理思維導圖,使得學生站在系統的高度對信息進行概括、壓縮和整合,把握數學知識間的聯系,體會數學思想方法,擴大“元”知識和“元”方法,形成良好的認知結構。
四、 基于邏輯連貫的教學反思
雖然數學的發展極其不合邏輯的,但是學生學習數學的過程與數學發展的歷程具有“同構性”,建構邏輯連貫的學習過程,目的是使學生縮短多元聯結知識的時間,拓展有深度的思維空間,為學生的生長謀求長遠利益的發展。
(一) 回歸本源性知識的教學
要教給學生什么層面的知識,是知識層面,是思維層面,還是文化層面?思考此問題是教學設計的起點,也是課堂教學實踐的著力點。備課時老師要回歸學生思維的起點,前后貫通地挖掘教材中一節課的價值。此節課中,深入解讀編者意圖,拓寬學生閱讀的視角,讓學生在收集、查閱文獻中領悟勾股文化的燦爛,在交流過程中將顯性的勾股定理知識與緘默的思維、方法、文化有機聯合,在交流互動中達到師生思維場的同頻共振。
(二) 讓學體驗知識的生成
哲學家海德格爾說過:教難于學,乃因教所要求的是讓學。讓學要老師理解何為讓學?什么地方讓?怎么讓?把知識的發現權,知情權讓給學生,讓學生去收集資料,讓學生去查閱勾股歷史文化,讓學生自己去理解,讓學生去展示交流,讓學生大膽地講述自己的奇思妙想,讓學生去整理知識,體會知識的形成和深化,老師學會傾聽,追問,留白,忘記預設,順應學情。
(三) 探究關注知識的生長點
1. 先行組織查閱,激活知識“固著點”
以任務驅動形式,利用網絡或書籍課前查閱,整理成非連續的引導性材料,了解勾股定理的歷史文化,架設新舊知識間的“認知橋梁”,為后續學習提供理想的“固著點”,激發有意義學習的心向。
2. 探究數學問題,建構合適“潛在距離”
利用先行組織者植入或激活的基礎上,對勾股定理與圖形面積關系的探究進行自然而然的生長,建構合適的新舊知識聯結的“潛在距離”,對知識進行同化,使得新知識獲得意義,舊知識得到鞏固、修正而獲得新的意義。生9解決的問題,知識固著點與新問題的潛在距離比較遠,探究的難度比較大,很多學生只能滿足驗證結論的狀態。生10不能解決的問題,也屬于潛在距離比較遠。短距聯接能漸進分化完成,長距聯接更多靠學生的創造智慧。
參考文獻:
[1]章建躍.數學教育隨想[M].杭州:浙江教育出版社,2017.
[2]顧泠沅.教學改革的行動與詮釋[M].北京:人民教育出版社,2006.
[3]卜以樓.“再探冪的運算”教學設計[J].江蘇教育,2017(2).
作者簡介:
王黎明,浙江省杭州市,浙江省杭州濱和中學。

