追問,讓數學思維向更深處漫溯
蔣亞燕

[摘要]問題是思維發展的砥礪石,更是學生數學素養不斷積累的關鍵點。為此,在日常教學中教師應利用追問誘發學生聯想,使學生的數學思維更加開闊,并設計合適的體驗情境,促使學生的學習理解更加深刻,從而實現思維的飛躍,促進他們綜合素養的不斷提升。
[關鍵詞]追問;數學思維;數學素養
[中圖分類號]G623.5 [文獻標識碼]A [文章編號] 1007—9068(2019)32—0035—02
數學教學的主要任務不僅是基本知識、基本技能的傳授,更重要的是促進學生積累豐厚的數學活動經驗,發展學生的數學思維,從而使其具有發現問題、提出問題、分析問題、研究問題的能力。學生的數學學習是一個富有創造性的過程,所以通過追問引領學生進行學習和反思,勢必會使動手實踐、自主探索和合作交流等數學學習活動更具活力,也會促使學生的數學思考有效發散,向縱深處漫溯,讓數學學習充滿情趣,閃爍著智慧的光芒。
一、誘發聯想,追問使思維開闊
積極的聯想是有效數學學習的利器之一。當學生能夠依據眼前的學習內容聯想到相關聯的知識點或學習活動過程,那么他們的思維也會隨著聯想而靈活開闊起來。因此,在數學教學中,教師要找準每一個知識點的來龍去脈,科學地進行預設,并設計有序的知識階梯,促使學生能夠感受到知識的生長點,從而進行合情的、有效的聯想,使既有的知識、經驗、技能、思維方法等成為有效學習的敲門磚,成為終身學習的基本積累。
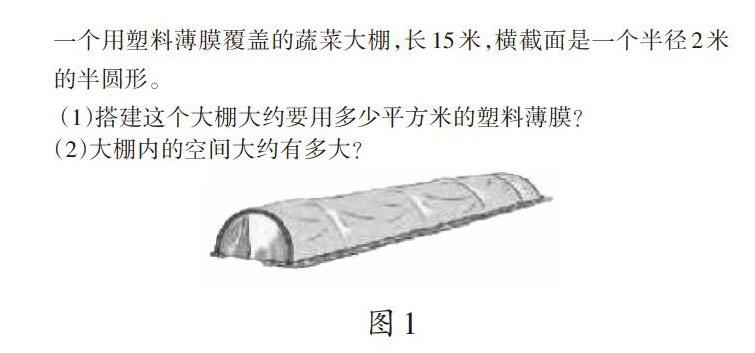
如在“圓柱的表面積和體積”練習課中,教師出示書中的習題:
師:你能根據題目中的數據去解決問題嗎?(學生自主練習,并進行交流)
生1:搭建大棚需要的薄膜面積就是大棚的表面積,對應圓柱表面積的一半。
生2:對!前后的半圓相當于圓柱上下底的一半,頂棚的薄膜相當于圓柱側面積的一半。
生3:體積也是圓柱體積的一半。
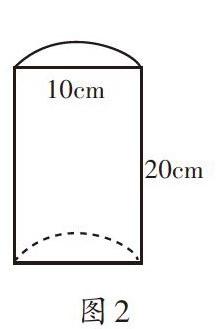
生4:我看到過這樣的一道習題(如圖2):(1)給這個積木表面涂油漆,要涂的面積是多少平方厘米?(2)這個積木的體積是多少立方厘米?它和剛才的大棚的計算方法一樣嗎?
(看到學生的問題,教師首先引導學生自主思考,再引導小組進行辨析。)
生5:計算體積的方法一樣,都是計算圓柱體積的一半。涂油漆要求表面積,這里的長方形面積是要計算的,而大棚的地面是種蔬菜的,不需要鋪薄膜,所以兩者的表面積計算方法不一樣。
師:你的分析很到位,很準確。對于這個積木的體積,你有其他的思考嗎?
生6:可以橫向對等切開,再拼起來,就是一個底面直徑為10厘米、高為10厘米的圓柱體了。
有效追問,能夠誘發學生展開聯想,使其數學思維向更廣闊處延伸。案例中教師的追問,使得大棚的體積與所用薄膜的面積的特征愈加明顯,不僅能促進學生對相關知識的回顧、運用和積累,同時還豐富了學習的內容,開闊了學生的認知視野,讓學生在比較中發現知識的異同,在研究中獲得更豐富的感知,有效地幫助學生建構數學認知。
二、以用促思,追問使思維深刻
數學學習的目的是積累知識經驗,形成技能技巧,發展數學思維,但最終目的是使學生能夠運用知識技能去發現問題、研究問題和解決問題,從而實現思維的發展。因此,教師要引導學生進行必要的數學練習,使其在練習中學會思考,學會梳理總結,進而獲得重要的數學思想方法,使數學思維在訓練中變得愈加犀利、深刻。
如“找次品”的教學片段:
師:經過上面的研究和學習,老師想了解大家的數感水平,看看誰的反應快、思考深。在27個同樣的零件中有一個次品是偏輕的。給你一個天平,至少稱幾次保證能找出次品呢?
(學生進行小組討論)
生1:要4次,27→(13、13、1)→(6、6、1)→(3、3)→(1、1、1)。
生2:3次就可以了,27→(9、9、9)→(3、3、3)→(1、1、1)。
師:大家看看,誰的思考更有道理?
(學生再次比較兩個同學的稱量過程,得出結論——至少3次)
師:27個零件只要3次。如果是81個這樣的零件中也有1個次品呢?
(學生運用獲得的經驗去思考)
生3:4次就夠了,81→(27、27、27)→(9、9、9)→(3、3、3)→(1、1、1)。
師:這么少的次數啊!還記得剛上課時,大家討論2187個零件中有1個次品需要稱幾次,有同學說需要2185次。現在,你是怎樣想的呢?
(學生討論,得出只要7次:2187→(729、729、729)→(249、249、249)→(81、81、81)→(27、27、27)→(9、9、9)→(3、3、3)→(1、1、1))
生4:我發現要使得稱的次數最少,應盡可能平均分成3份。
縱觀整個教學活動,執教者匠心獨運。課前,以猜猜2187個零件來熱身,在繁雜的數據刺激下讓學生的思維預熱起來;課始,通過3個零件的實踐稱量,得出(1、1、1)分法,再拓展到9個零件。面對9個零件,不同的學生會有不同的思考實踐,當“9→(4、4、1)→(2、2)→(1、1),3次”和“9→(3、3、3)→(1、1、1),2次”等不同的思路呈現時,學生通過比較,深刻地體會到“至少稱幾次”的基本要義和優化策略的價值。課中,教師引導學生解決上述案例中的幾組問題,使得優化策略深深烙印在學生的腦海中。
教師有意識地引導學生運用在9個零件中找出次品的經驗和方法,去思索27個零件、81個零件的情況,最后照應到上課前的熱身思考題的2187個零件,使數學思考呈現階梯性,讓學生在問題突破中感受到思考的魅力。其間教師的不斷追問極具活力,一個又一個富有思考性的問題被拋出來時,學生的驚訝、感嘆與震撼之情也隨之而來,學生被數學的神奇魅力所感染,從而使數學學習具有了更強的挑戰性和趣味性,無形之中使學生的數學思維獲得質的飛躍。
三、以評激思,追問使思維敏捷
發揮評價的激勵作用,以此促進學生的思維發展,也是有效教學策略之一。適宜的、恰當的評價,能夠改善課堂的質態,有利于學生積極思考,提升學生思維的靈活性,使得學生數學思維向更深處漫溯有了基礎。
如“三角形的面積公式推導”教學片段:
師:剛才計算了長方形、正方形、平行四邊形的面積,那圖3的面積,你會求嗎?
(學生看到圖形,提出不同觀點)
生1:這是個三角形,它的面積計算公式還沒有學過。
生2:老師,三角形的面積計算是不是我們今天要學習的內容啊?
師:是的!我們今天會研究三角形的面積計算。你能運用長方形、正方形或平行四邊形的面積計算方法先思考一下嗎?
(學生積極思考,動手操作)
生3:我把正方形沿對角線剪開,得到2個一樣的三角形,所以三角形的面積等于正方形面積的一半,即邊長乘邊長除以2。
生4:我把長方形剪成兩個一樣的直角三角形,其中一個三角形的面積等于長方形面積的一半,即長乘寬除以2。
生5:平行四邊形也可以剪成2個一樣的三角形,因為平行四邊形的面積等于底乘高,所以我們先要找準三角形的底和高,發現它們與平行四邊形的底和高重合。這樣一個三角形的面積就等于底乘高除以2。
師:老師發現了一個有趣的現象,大家得出的三角形的面積都要除以2,這是為什么呢?
生6:我們都是把圖形一分為二,那么得到的三角形的面積只是原來圖形面積的一半。
師:對的。那能不能反過來進行一種新的嘗試呢?
(學生在教師的追問中,進行嘗試性操作)
生7:我們小組發現用2個完全一樣的三角形可以拼成一個長方形、一個正方形或一個平行四邊形,可見一個三角形的面積就是拼成圖形面積的一半,所以三角形的面積等于底乘高除以2。
評價是學習的催化劑。如果教師能夠掌控好這一利器,就一定能開啟學生的心扉,增強學生的學習信心,也會激活學生的學習思維,讓數學課堂洋溢著無盡的活力。案例中教師不惟教材的編排,而是順勢利導,引導學生用既有的圖形面積計算過程去想象,以獲得最直接的感知。同時,利用恰當的評價,激勵學生去思考,“老師發現了一個有趣的現象,大家得出的三角形的面積都要除以2,這是為什么呢?”這句話既肯定了學生的活動成果,又給學生開啟了一扇新的思考之門。因此,在數學教學中,教師要時刻關注學生的學習質態,多站在學生的立場上去審視學生的活動。長此以往,學生就有信心去發現問題,有勇氣去提出問題,也會更加縝密地思考,精心組織語言來表達自己的所思所想,思維也會隨著學習的深入而不斷深刻。
綜上所述,用好課堂追問這一利器,能夠促使學生對學習更為關注,促進其獨立思考的深入,誘使其學習靈感的萌發,更是改善課堂學習格局、激活學生思維,逼近知識本質內核的“導火線”。因此,在數學教學中,教師應敏銳地發現、捕捉生成信息,善假“意外”因素巧追問。同時,還要引發學生的有效追問,讓他們在追問中學會思考,在思考中開啟智慧、引發創新。長此以往,學生的思維會在追問中邁向更開闊的“原野”!
(責編 羅艷)

