在數學命題探究中提升數學思維

徐飛

[摘? 要] 數學命題是數學知識體系的重要構成，在初中數學教材中涉及很多的數學命題. 對于數學命題的教學，要走出傳統“拋售”式教學的誤區，要引導學生經歷“數學猜想——操作驗證——數學證明”的過程，以此促進學生在探究數學命題的過程中達到提升數學思維能力的目標. 基于此背景，文章對“四邊形內角和”一課的教學進行了探究，希望能夠為廣大教師提供一定的借鑒.

[關鍵詞] 數學命題;探究學習;數學思維;四邊形內角和

在初中數學教材中，涉及很多的數學命題，這一些數學命題是學生進行數學證明、數學解題的重要依據之一. 很多教師在教學中會直接把數學命題拋給學生進行記憶，導致學生就不能夠理解數學命題的本質，從而造成了數學命題學習的被動化與膚淺化. 數學命題是一種數學判斷，在數學命題教學中，教師要善于引導學生經歷對數學命題的探究過程，這樣，就能夠有效地促進學生數學思維能力的提升. 以下結合“四邊形內角和”一課的教學進行論述.

■ 激活原有認知，引導類比遷移

數學知識之間是存在緊密聯系的，在初中數學教學中，教師要激活學生原有的認知經驗，以此引導學生進行類比遷移，這樣，就能夠有效地為培養他們的數學思維奠定基礎.

初中生在學習四邊形之前，已經學過三角形的相關知識，本課教學的第一個環節是讓學生對四邊形的定義及特征進行學習. 因此在教學中，筆者先利用多媒體給學生出示交通警示牌（三角形）、廣告牌（四邊形）、螺絲帽（六邊形）.

師：從這一些物體的表面能夠抽象出什么幾何圖形？

生：從這一些物體的表面能夠分別抽象出三角形、四邊形還有六邊形.

師：在數學上是如何定義三角形的？

生1：三角形就是三條線段連接而成的圖形.

生2（補充）：三條線段首尾順次連接，這種圖形稱之為三角形.

生3（再補充）：由不相同直線上的三條線段首尾順次連接所形成的圖形稱之為三角形.

師：你能夠根據三角形的定義，通過類比的方式對四邊形進行定義嗎？

生3：不在同一條直線上的四條線段首尾順次連接所形成的圖形叫四邊形.

師（大屏幕出示一個四邊形ABCD）：那么四邊形有幾條邊、幾個角、幾個頂點呢？

生4：四邊形有四條邊、四個角以及四個頂點.

在這一教學片段中，教師先引導學生根據實物抽象出三角形、四邊形、六邊形這三個幾何圖形，然后引導學生對三角形的定義進行回顧，并在此基礎上讓學生通過類比對四邊形進行定義. 這樣的設計符合學生的認知規律，可以讓學生在原有的認知經驗上把握四邊形的定義及基本特征，同時，為學生自主探究四邊形的內角和奠定基礎.

■ 基于動手操作，初步感知命題

初中生在學習數學知識的過程中，是遵循“形象感知——抽象提升”這一規律的，動手操作是他們對數學知識進行形象感知的重要途徑. 因此，在數學命題的教學中，教師要善于引導學生開展動手操作活動，讓學生在動手操作的過程中對數學命題進行初步感知.

師：請大家在本子上畫出一個四邊形. （學生畫圖）

師：你覺得在你畫好的四邊形中，四個內角一共是多少度？

生5：我覺得是360°.

生6：我覺得一個四邊形可以分成兩個三角形，所以四個內角的和應該是360°.

師：你是否可以驗證這一結論呢？（學生思考并進行操作驗證）

生7：我是把自己畫的四邊形的四個內角剪下，然后進行拼接，在拼接的過程中保證四個角的頂點和邊重合，最后拼成了一個周角，說明四邊形的內角和是360°.

生8：我是把畫的四邊形的四個內角的度數用量角器量出來，然后加起來也是360°.

師：同學們，你們真厲害，通過剛才的學習發現了一個數學命題：四邊形的內角和等于360°. （板書）

在這一環節中，教師引導學生進行動手操作能使其對四邊形有更加直觀的認知，隨后猜想四邊形內角和是360°. 然后，再引導學生對這一猜想通過拼一拼、量一量的操作進行驗證，從而發現了“四邊形的內角和等于360°”這一命題.

■ 基于原有命題，引導證明命題

在初中數學教學中，培養學生的高階數學思維是十分重要的. 數學證明是一種高階的思維活動方式，引導學生對命題進行證明是關鍵環節. 在學生對“四邊形的內角和等于360°”這一命題進行操作驗證之后，引導學生基于“三角形的內角和是180°”進行證明. 教學中，筆者是這樣對學生進行引導的：

師：剛才你們通過操作驗證了“四邊形的內角和等于360°”這一命題. 那么，你們能不能結合已知的命題對這一命題進行證明呢？

生9：我覺得可以在“三角形的內角和是180°”這一命題的基礎上進行證明.

師：你的想法真好，這樣進行證明的關鍵點是什么？（學生討論）

生10：把四邊形轉化為三角形是關鍵點.

師：那么，怎樣才能把四邊形轉化成三角形呢？

生11：可以通過畫輔助線的方式把四邊形轉化成三角形.

在證明“四邊形的內角和等于360°”這一命題時，轉化是重要的方法，以上教學環節中，教師通過引導讓學生明白添上輔助線會使題目顯得相對簡單. 在這個過程中，能讓學生深度體會證明思路的轉化，提升學生的推理水平.

師：接下來，大家就根據剛才的思路對這一命題進行證明.

（學生自主證明命題. 在這一過程中，教師在學生之間巡視，為有困惑的學生提供幫助和點撥，當學生完成證明之后，教師組織學生反饋）

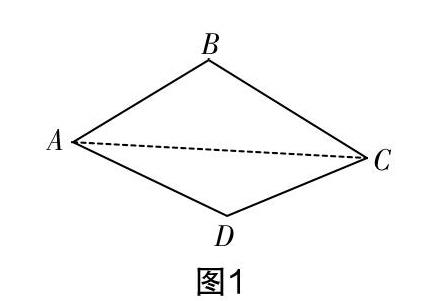
生12：如圖1，連接AC，這樣就把四邊形ABCD分割成了三角形ABC和三角形ACD，一個三角形的內角和為180°，兩個三角形的內角和就是360°，所以四邊形ABCD的內角和是360°.

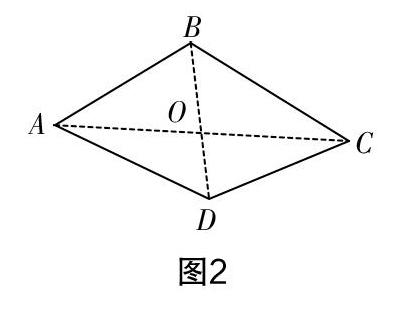
生13：如圖2，將AC，BD相連，此時四個三角形的內角之和為4×180°=720°，隨后將四邊形之中的周角減去，得到4×180°-360°=360°.

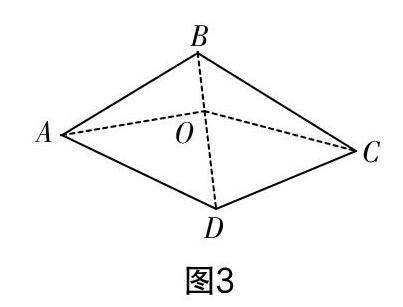
生14：如圖3，在四邊形內確定一點O，連接AO，BO，CO和DO，圖中四個三角形的內角和是4×180°=720°，將四邊形內周角的度數減去，得到4×180°-360°=360°.

生15：如圖4，在四邊形外確定一點O，連接AO，BO，CO和DO，圖中△OAB，△OAD，△ODC的三個內角之和是3×180°=540°，將△OBD內角和的度數減去，得到3×180°-180°=360°.

生16：如圖5所示，將BC延長，在延長線上確定一點E，連接AE，交CD于點F，得∠BCD=∠E+∠CFE=∠E+∠AFD，此時四邊形內角和等于△ABE與△ADF的內角和之和，為360°.

以上5種方法均先讓學生自主思考，然后讓他們在小組內對證明的過程進行交流討論. 這樣，學生就能夠在互動學習的過程中引發思維碰撞，從而開闊其證明思路，拓展他們的數學思維空間.

總之，數學命題是初中數學知識體系的重要構成，在“核心素養”理念下，對于數學命題的教學，引導學生經歷“數學猜想——操作驗證——數學證明”的過程十分重要，這樣，才能在這個過程中促進他們數學思維能力的有效提升.