高中數學課堂教學中培養學生解題能力的策略

梁貧

【摘 要】本文以直觀想象素養培養為支點，解讀數形結合與解題能力的關系，論述利用數形結合思想培養學生解題能力的策略：激發興趣、喚醒學生對數形結合的關注;多元途徑、聚焦問題以提高解題能力。

【關鍵詞】高中數學 解題能力 數形結合

《普通高中數學課程標準（2017 版）》（下文簡稱《數學標準》）明確指出“數學是研究數量關系和空間形式的一門科學”，換言之，高中數學解題能力培養的關鍵在于“數”“形”兩類要素及相互關系上。借助數形結合思想，不僅可以有效地構建“數”和“形”的內在聯系，而且能便捷地建立解決數學問題的直觀模型，從而降低問題理解難度、獲取問題解決方法。值得注意的是，解題能力不能等同于解題技巧，《數學標準》在高中數學考核的命題原則中指出：“注重數學本質、通性通法，淡化解題技巧，融入數學文化。”尤其在高中數學課堂教學過程中，如果混淆解題能力和解題技巧的概念，那么容易將數形結合思想退化成數形結合工具。

一、以直觀想象素養培養為支點，數形結合與解題能力的關系解讀

結合高中數學課堂教學實際，數形結合是一種數學思想，但大多數情況下，又被視為一種具體方法。換言之，數形結合的理論性、實踐性特征是高度融合的。這就要求教師在高中數學課堂教學解題能力培養過程中，合理把握數形結合理論價值、實踐價值的平衡性，避免學生將其視為一種狹隘的解題工具。《數學標準》明確指出“直觀想象是發現和提出問題、分析和解決問題的重要手段”，同時又指出，要培養學生數學直觀想象核心素養，數形結合是一種必然的渠道。以“形”的具象化功能，將“數”的關系表達出來，反之，利用“數”的抽象化功能，將“形”的關系進行概括、簡化。據此可將直觀想象核心素養作為一個支點，形成“數形結合（起點）→直觀想象（支點）→解題能力（終點）”的邏輯思維模型。這樣，在以數形結合作為起點向直觀想象這一支點的發展過程中，就能有效地保證數形結合作為一種數學思想的價值;并在進一步向解題能力這一終點發展的過程中，體現數形結合作為一種數學方法的作用。

二、以課堂教學模式為前提，利用數形結合思想培養學生解題能力的策略

（一）激發興趣、喚醒學生對數形結合的關注

立足我國學校教育視閾之下，數學課程中采取數形結合思想方法進行解題是一種常態。高中生可以持續初中階段數形結合的應用規律，自主進行探索。但對于老師來說，在高中數學課堂教學中要注意結合教材知識點，創設豐富情境來激發學生興趣，進一步喚醒學生對數形結合的關注。

1.現實生活情境。根據認知情境理論，知識并非“事實與規則的集合”，而是人與環境之間的“動態建構與組織”，學習者（個體）為與外界達成相對協調的交互狀態，就必須不斷調整自己的適應力。從這一點出發，借助生活情境能夠更好地提高學生解題能力。例如，在高中數學“統計與概率”的教學過程中，可以通過列舉“彩票中獎號碼”“選舉投票預測”等生活中存在的事物，將其轉化成數學問題，并結合數形結合思想加以解決。當然，在高中數學課堂教學模式下，生活情境的概念需要狹義化，以便將數形結合思想應用于解題能力培養的過程中。可借助生活氣息情境輔助開展數學活動，進行交流、探討。例如，教師可以利用生活中的電源開關中的“開”和“閉”代表數學邏輯中的“且”和“或”，并畫出相應的圖進行展示，以便活到更好地理解數學中“且”和“或”的概念。

2.數學文化情境。《數學標準》指出“數學承載著思想和文化，是人類文明的重要組成部分”。但大多數情況下，數學文化在高中數學課堂教學活動中被邊緣化，尤其在解題能力培養過程中，數學文化的價值很少被重視。事實上，數學雖然是自然學科，是理性的，但它仍然有獨特的人文性特質。例如，從“形”來看，數學“形”的審美價值，具有和諧美、對稱美;從“數”的角度看，具有抽象美、簡潔美。創設數學文化情境，有利于學生貫通數形結合的原理。例如，在函數的基礎上進行表達式變形，能夠形成與之對應的曲線圖形，能夠讓學生深刻感知數學魅力。

3.游戲、故事情境。解題能力的培養是循序漸進、久久為功的，同樣，喚醒學生對數形結合思想的關注，不可一蹴而就。考慮到高中數學課堂教學內容資源、時間、工具等條件限制，我們往往無法開展大規模的實踐體驗活動。因此我們可通過游戲、故事情境創設等，沖淡高中數學的枯燥乏味之感，不斷維持學生的學習興趣。

（二）多元途徑、聚焦問題以提高解題能力

1.從“文本概念”到“數形概念”的解題能力培養。概念是高中數學知識體系的基本構成要素，也是高中數學課堂教學中的基礎講解對象。從教材內容組織形式出發，概念大多以文本形式呈現，具有高度概括性、抽象性、符號性的特征。對于學生而言，對此有較高的理解難度。如果將概念直接作用于解題能力培養，那么很難發揮概念作為知識點的數學價值。因此，可借助數形結合思想來闡釋數學概念，提高其在解題過程中的應用效率和效果。

以高中數學中“橢圓”概念為例，教材中給出的定義為“平面內與兩個定點 F1、F2 距離之和等于常數（大于|F1F2|）的點的軌跡”。顯而易見，在這種文本概念的描述形式下，學生很難產生直觀想象的畫面。我們知道，文本概念是純粹的數量關系，軌跡是“點的集合”，也就是動態的點累積形成的圖形。如果引入數形結合思想，那么就可以將橢圓概念進一步形象化。教師可通過指導學生進行如下實踐獲得體驗：首先，取一張白紙，按照文本概念的要求，在任意位置上標注兩個點 F1、F2，然后再確定一個“常量”，可以用一段大于|F1F2|的細線代替。將細線的兩端固定在 F1 和 F2 上，繃緊細線形成一個非等邊三角形（必要條件）。然后讓學生在細線上固定筆尖、以繃緊狀態運動，觀察閉合后的圖形狀態，即得到橢圓圖形。這個過程直觀地完成了從“文本概念”到“數形概念”的轉化。

理解數學概念是解決相應數學問題的前提，在上例中，如果學生能透徹地理解橢圓概念，那么學生將能更好地理解接下來要學習的雙曲線、拋物線概念。事實上，“文本概念”到“數形概念”轉化的過程并不復雜，如上例通過動手操作畫橢圓，就是一種從概念的“數”形式向“形”形式進行的一種數開結合思想，它能極大地減輕理解負擔，并在轉化過程中，使學生更清晰地理解橢圓的幾何意義，P={M||MF1|+|MF2|=2a} 內涵。

2.“經典例題”與“經典錯誤”的解題能力培養。顧名思義，解題能力面向的是“題”，數形結合思想作用對象也應放在“題”本身。高中數學課堂教學中接觸的題型，以經典例題和經典錯題兩類為主，其中，經典例題又和概念、定理、模型等存在密切的關系，甚至直接源自某一知識點的轉化。學生通過掌握經典例題的解法思維、技巧，可在同類型解題過程中做到事半功倍。以經典錯題為基礎的解題能力培養，本質上是一種糾錯、避錯素養培養，旨在發揮“引以為戒”的作用。數形結合思想方法在應用過程中，對這兩種題型需要進行區分對待。相對而言，通過經典錯題提升學生解題能力，既可以強化學生對知識點的掌握，又可以有效規避常見錯誤，更適合在課堂教學模式下應用。

例如，變量 x 和 y 滿足約束條件 ，則目標函數 z=x+2y 的最小值是。

A.2? ? B.3? ? C.4? ? D.5

學生容易受到慣性思維的影響，在利用數形結合思想解題時，根據題目簡單地畫出圖形，然后得出答案。在上面問題中，最常見的錯誤是選擇答案“A.2”，其理由見下圖 1。

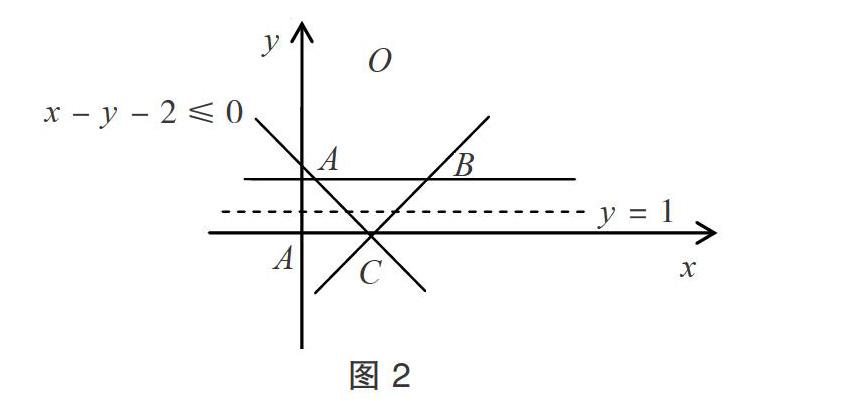
但是稍微觀察就不難發現，當動直線經過 C（2，0）時，明顯不符合 y≥1 的要求。如圖 2 所示，需要將 C 排除在可行域之外，正確答案應該為“B.3”。以上題目的“經典錯誤”在于，在進行數形結合過程中沒有充分地將“數”和“形”的條件進行匹配。

3.“數形轉化”向“數形結合”轉換的解題能力培養。鑒于高中數學知識點多、內容抽象、關聯度高的特征，所謂解題能力，本質上是學生面對題目時的分析能力、歸納能力、推理能力、計算能力等一系列綜合能力，它的形成是一個從量變到質變的積累過程。同樣，數形結合思想下的解題能力培養，需要經過一定的學習過程。整體上可歸納為數形轉化向數形結合轉換，其中，數形轉化是一個相互逆轉的過程。教師要讓學生充分理解，由數向形的轉化是“抽象—具象”的過程，重點在于降低理解難度、形成直觀體驗;而“由形向數”的轉化則是“具象—抽象”的過程，其價值在于整合問題已知條件、形成解題步驟、獲取正確答案。建立在高中數學課堂教學中的數形轉化能力訓練，可與具體知識點結合，注重功在平時。例如，在講解圓錐曲線類問題時，要善于運用圖形表達形式來闡釋性質;在學習“點、直線、平面之間的位置關系”時，要善于運用向量、平行、相交等符號進行表達，讓學生在熟練掌握數形轉化之后，再謀求解決問題過程中的數形結合應用，這樣方能循序漸進地提高解題能力。

高中階段數學解題能力的培養是一個動態發展過程，可運用的解題思想、方法很多。本文主要從“直觀想象”這一核心素養切入，倡導數形結合思想方法的應用。在具體策略方面，可從兩個方面同時展開。其一是喚醒學生對數形結合的關注，唯有意識上形成重視，才能在行動上落實。其二是聚焦問題本身提高解題能力，無論是面向概念、定理，還是經典例題、錯題，以數形結合思想培養學生解題能力，都要落實在具體問題層面上。

【參考文獻】

[1]李國燾.高中數學課堂教學中學生解題能力的培養探討[J].學周刊，2020（04）

[2]陳 巖.高中數學教學中學生解題能力的培養策略[J].西部素質教育，2018，（4）

[3]王錄金.高中數學教學中學生解題能力的培養策略[J].數學學習與研究，2018（12）

[4]莊海軍.高中數學課堂教學中學生解題能力的培養策略[J].中國校外教育，2017（08）

[5]丁紅梅.新課程背景下高中數學課堂教學中學生創新思維能力的培養策略[J].中國校外教育，2015（22）

【作者簡介】梁 貧（1977— ），女，漢族，籍貫廣西興業，中學一級教師，現就職于玉林市興業縣第二中學，研究方向為數學教學。

（責編 盧建龍）