高中數學教學中數形結合思想運用策略探究
金正


摘要:數形結合既是一種數學思想,也是一種教與學的方法,可以激活思維,將抽象問題具體化、復雜問題簡單化。它是將數學問題中的數或者數量關系,以圖形的形式進行充分表現,借助圖形研究數量關系,展開問題探索。要知道在高中數學教學中,教育教學要以培養學習能力,提高解題效率和解題質量為目標,在掌握數學思想的同時培養數學素養。為此,本文從數形結合的角度出發,針對高中數學教學模式進行了策略探索,旨在通過以數解形,以形探數教學中提高學習能力。
關鍵詞:高中數學;數形結合;運用策略
高中數學新課程改革中明確提到:在教學中要提高學生對數學思想的認識,使其能夠運用數學思想探索問題本質,提高解題質量和解題效率。而數形結合作為數學思想的重要組成部分,是通過數和形的探索,促使其能夠在數學問題解決中得到思維能力的培養,不僅可以提高課堂教學效果,還可以培養學習方法,提高學生對數學知識的綜合運用能力。為此,本文從數形結合思想的視角出發,針對高中數學教學模式策略進行了探究分析。
一、應用數形結合,探究三角函數性質圖像
在高中數學教學中,運用數形結合的思想,首先教師要充分考慮數與形的對應管轄,在等價性探索中,認識數學問題的本質,提高問題解決能力,要知道在三角函數數學探索學習中,涵蓋了九組誘導公式、正弦、余弦、正切等函數圖像和性質,倘若運用死記硬背的方法,不僅會激發厭學情緒,還會降低教學質量。為此,面對函數記憶、認識函數性質等問題時,可以采用數形結合的方法作為教學輔導。例如,在教學“三角函數的性質與圖像”數學內容時,在認識y=sinx函數性質與圖像的時候,可以利用生活中摩天輪的畫面為輔助,進行圖形搭建,如
以摩天輪轉輪中心為原點O,以水平線為橫軸,建立平面直角坐標系,設O到地面的高度OT為l,P為轉輪邊緣上的任意一點,半徑為OP為r,記以OP的終邊的角為x rad,點P離地面的高度為y,思考函數有什么性質。在數形探索中認識正弦函數圖形性質,引導學生繪制y=sinx圖像,結合圖像分析其單調性、周期、值域,讓學生運用數形結合的方法對y=cosx、y=tanx等函數圖像進行問題解析。
二、利用數形結合,有效制定數學解題方案
數形結合思想在高中數學解題中有著廣泛的運用,它可以提高學生的審題分析能力,強化理解,精準解題思路,對解題效率和解題質量的提高有著重要的促進作用。為此,在高中數學教學中,可以利用數形結合思想制定解題方案,提高自主學習能力和問題分析能力。例如,在教學《直線與平面平行》數學內容時,會遇到以下類型的例題如:已知三棱錐A-BCD中,E、F分別為AB、AD的中點,過EF的平面截三棱錐得到截面為EFHG,求證EF//GH。在解題的時候,倘若依據題意直接答題,必然會出現思維混亂的現象,那么,在這個時候,可以依據題意進行圖形搭建,如:
在圖形搭建中,結合已知條件,制定解題方案,如第一步,可以依據△ABD,結合三角形中位線定理推導EF//BD,第二步,利用EF?面CD,BD?面BCD,線面平行判定定理推導EF//面BCD,第三步,依據線面平行性質定理,推論結論。在數形結合中優化解題思路,制定解題計劃,在數與形的談搜中提高解題質量。這樣既可以強化學生對數學思想的感悟,又可以通過數學問題的探索和數形結合思想分析,使得學生得到數學抽象、數據分析、邏輯推理等數學素養培養,在數形結合思想運用中提高課堂教學質量。
三、搭建數形平臺,提高對向量問題的理解
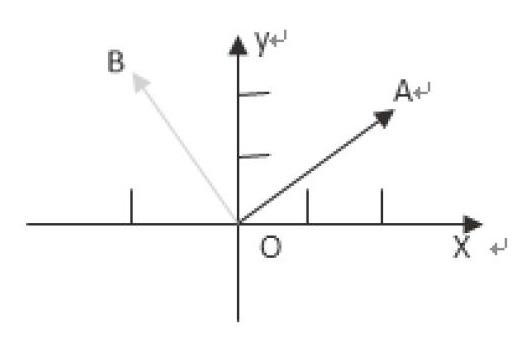
在高中數學教學中,向量問題一直以來都是數學教學的重點、難點,可以說是高考的必考內容,也是一個基本的重要的數學概念,既是代數的載體,又是幾何的載體。因此,在數形結合思想運用中,可以充分應用于向量問題中進行探索分析,用向量中的“大小”代表數,方向表示“形”聯系數形結合,解決結合問題,認識向量法。例如,在探索“用向量的坐標表示兩個向量垂直的條件”中這一數學內容的時候:已知點A(2,1)將向量OA繞原點O逆時針旋轉得到OB,求B點的坐標。在解析的時候,可以搭建數形平臺,如:
通過數形平臺的搭建,分析結合已知條件,得出|OB|=|OA|,OA·OB=0,再假設B坐標為(x,y)結合OA(2,1),聯立方程組展開問題探索和解決。在數形平臺搭建中,運用數形分析問題,探索數量關系,探尋向量特點和解題思路。在數形結合中搭建代數和幾何的橋梁,發現圖形內部存在的向量關系。提高數學建模能力和直觀想象能力。最終實現高中數學高效課堂的構建,培養學生數形結合數學思想。
四、結語
高中數學教學中運用數形結合的思想,可以提高解題質量和解題效率,鍛煉數學思維,培養數學綜合素養,在數與形中分析數量關系,探尋數學本質。為此,教師可以通過數形結合,認識函數性質、制定解題方案、理解向量問題,使得學生能夠在高中數學學習中,真正通過數與幾何的探索,掌握數學思想,提高學習能力。
參考文獻:
[1]石翀.淺析數形結合思想在高中數學教學中的應用[J].甘肅教育,2020 (06):74.
[2]張文濤.試談數形結合思想在高中數學教學中的運用[J].數學學習與研究,2020 (04):25.

