基于問題導(dǎo)向的高中數(shù)學(xué)概念復(fù)習(xí)策略探究

曾慶文

摘要：數(shù)學(xué)概念是數(shù)學(xué)知識體系的重要組成部分，也是數(shù)學(xué)定理、公式、法則的最基本組成單位。在高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)中，以問題為導(dǎo)向進(jìn)行教學(xué)優(yōu)化，要注意問題設(shè)計(jì)的有序性、層次性、廣度性、深度性，在有效問題分析、探索的基礎(chǔ)上提高對概念的理解，強(qiáng)化復(fù)習(xí)學(xué)習(xí)思路，提高數(shù)學(xué)概念復(fù)習(xí)教學(xué)效果。為此，本文分析了問題導(dǎo)向下的高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)的意義;探究了其引導(dǎo)教學(xué)原則;解讀了復(fù)習(xí)提升策略。

關(guān)鍵詞：問題導(dǎo)向;高中數(shù)學(xué);概念復(fù)習(xí);能力提升

中圖分類號：G633.6?文獻(xiàn)標(biāo)識碼：A文章編號：1992-7711（2020）20-032-2

學(xué)生通過概念的學(xué)習(xí)和理解，不僅可以促進(jìn)對數(shù)學(xué)重難點(diǎn)知識的消化，還可以構(gòu)建全新的認(rèn)知結(jié)構(gòu)，實(shí)現(xiàn)深度學(xué)習(xí)，提高數(shù)學(xué)問題解決能力。而問題教學(xué)法的設(shè)計(jì)應(yīng)用，不僅可以構(gòu)建和諧的師生關(guān)系，激發(fā)自主探究學(xué)習(xí)興趣，還可以加深對概念的理解。為此，本文以問題為教學(xué)前提，以高中數(shù)學(xué)概念復(fù)習(xí)為核心，以提高數(shù)學(xué)學(xué)習(xí)能力，培養(yǎng)良好復(fù)習(xí)學(xué)習(xí)方法為目標(biāo)，分析了問題導(dǎo)向下的高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)的意義;探究了其引導(dǎo)教學(xué)原則;解讀了復(fù)習(xí)提升策略。

一、基于問題導(dǎo)向的高中數(shù)學(xué)概念復(fù)習(xí)的意義

1.有利于激活思維促進(jìn)數(shù)學(xué)學(xué)習(xí)理解

數(shù)學(xué)概念是學(xué)好數(shù)學(xué)、掌握數(shù)學(xué)的前提，但是，也由于概念的抽象性，導(dǎo)致學(xué)生在理解概念的時候，對概念的發(fā)展過程或者實(shí)際應(yīng)用缺乏有效掌握。但是以問題為導(dǎo)向教學(xué)手段的應(yīng)用就不同了，旨在通過激活思維為前提，在有序的、層層的問題引導(dǎo)中，促進(jìn)對數(shù)學(xué)知識的理解和消化，不僅可以使其熟練運(yùn)用知識解決實(shí)際問題，還可以幫助其理清來龍去脈，增強(qiáng)學(xué)習(xí)體驗(yàn)感，在揭示抽象概念的過程中，促進(jìn)掌握學(xué)習(xí)方法，完善教學(xué)目標(biāo)。

2.有利于完善知識結(jié)構(gòu)提高問題解決能力

以問題為導(dǎo)向下的高中數(shù)學(xué)概念復(fù)習(xí)的教學(xué)目的是：引導(dǎo)其理清基本概念、原理、方法，明白知識的產(chǎn)生、形成的過程。在探索概念之間聯(lián)系的同時，由點(diǎn)成線、連線成面，完成知識充足，提高問題解決能力，通過深度問題引導(dǎo)探索，培養(yǎng)思維深度，使其以概念掌握為基礎(chǔ)，對數(shù)學(xué)問題有一個清楚的認(rèn)識。它的應(yīng)用和落實(shí)，不僅可以提高數(shù)學(xué)學(xué)習(xí)自信心，還可以為學(xué)生理解數(shù)學(xué)相關(guān)性質(zhì)定理，運(yùn)用數(shù)學(xué)公式、概念解決實(shí)際問題奠定堅(jiān)持的基礎(chǔ)條件。

3.有利于促進(jìn)深度學(xué)習(xí)提高課堂教學(xué)質(zhì)量

深度學(xué)習(xí)是提高課堂教學(xué)質(zhì)量的重要前提條件。在高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)中，以問題為導(dǎo)向，進(jìn)行教學(xué)設(shè)計(jì)，不僅可以引導(dǎo)其對數(shù)學(xué)概念、命題規(guī)律、學(xué)習(xí)方法有一個深度的認(rèn)識和掌握，還可以促進(jìn)深入學(xué)習(xí)，抓住問題的本質(zhì)，引導(dǎo)其從整體上分析問題、探討問題，形成科學(xué)的學(xué)習(xí)方法。為此，教師一定要重視問題教學(xué)法的運(yùn)用，重視概念復(fù)習(xí)教學(xué)，重視學(xué)習(xí)過程的優(yōu)化，在系統(tǒng)化的問題引導(dǎo)中，提高數(shù)學(xué)復(fù)習(xí)效果，培養(yǎng)數(shù)學(xué)素養(yǎng)。

二、基于問題導(dǎo)向的高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)原則

1.啟發(fā)性原則

在數(shù)學(xué)教學(xué)中，各個知識點(diǎn)之間有著潛在的聯(lián)系，每一個知識板塊都需要學(xué)生進(jìn)行層層分析，從而探尋其因果，提高理解。而數(shù)學(xué)概念作為學(xué)習(xí)數(shù)學(xué)的基礎(chǔ)，它是學(xué)生理解和消化的機(jī)器。因此，在概念復(fù)習(xí)教學(xué)的過程中，要注意啟發(fā)性的原則，啟發(fā)其聯(lián)合新舊概念進(jìn)行對比分析，啟發(fā)學(xué)生獨(dú)立思考、善于分析，啟發(fā)其構(gòu)建知識體系，圍繞概念探索問題，明晰命題本意。

2.發(fā)展性原則

在概念復(fù)習(xí)教學(xué)中，作為學(xué)習(xí)數(shù)學(xué)的基礎(chǔ)和核心，要從發(fā)展的視角設(shè)計(jì)問題，引導(dǎo)學(xué)生進(jìn)行自主探究，注重概念之間的關(guān)聯(lián)性，使其能夠在概念理解的基礎(chǔ)上舉一反三，提高數(shù)學(xué)思維能力，培養(yǎng)數(shù)學(xué)核心素養(yǎng)。

3.系統(tǒng)性原則

對數(shù)學(xué)概念進(jìn)行復(fù)習(xí)教學(xué)，其最重要的目的之一，是為了讓學(xué)生能夠在運(yùn)用概念分析問題的時候，可以精準(zhǔn)分析知識點(diǎn)之間的因果關(guān)系，快速找準(zhǔn)解題思路。為此，在教學(xué)的時候，要注意系統(tǒng)性的原則，從多角度對概念進(jìn)行問題設(shè)計(jì)引導(dǎo)，啟發(fā)學(xué)生能夠從多視角進(jìn)行概念分析，提高總結(jié)反思學(xué)習(xí)能力，促使對數(shù)學(xué)概念有一個深入的理解，從而提高自身學(xué)習(xí)數(shù)學(xué)的能力。

三、基于問題導(dǎo)向的高中數(shù)學(xué)概念復(fù)習(xí)策略分析

1.設(shè)計(jì)有序問題，認(rèn)識概念形成過程，激發(fā)復(fù)習(xí)學(xué)習(xí)興趣

俗話說得好“興趣是最好的老師”在概念復(fù)習(xí)教學(xué)中，有很多學(xué)生之所以掌握不好，是對概念形成過程缺乏有效理解，然后隨著難度的增設(shè)，在沒有打好地基的前提下，又去解決問題，自然而然學(xué)習(xí)質(zhì)量不會高。為此，為發(fā)揮問題引導(dǎo)教學(xué)方法的育人價值，教師要設(shè)計(jì)有序問題，在層層分析的過程中，培養(yǎng)科學(xué)的探索精神，促進(jìn)概念理解。例如，在復(fù)習(xí)概念《集合》數(shù)學(xué)內(nèi)容的時候，可以設(shè)計(jì)以下有序問題：

師：同學(xué)們，接下來，我們請全班的男同學(xué)站起來，這就是我們班男孩子的集合;請全班女孩子站起來，這就是我們班女生的集合

師：通過老師舉例，思考一下，一個班的男孩和女孩是一個？

生：小組、群體、集體

師：回答的非常精準(zhǔn)，集合就是一個集體，并且我們將組成這個集體的研究對象統(tǒng)稱為元素。在這里，我們可以看到，男孩的集合不包括女孩，女孩的集合也不會包括男孩，也就是說他們有自己的？

生：特點(diǎn)

生：特征

在有序問題引導(dǎo)中，認(rèn)識概念形成過程，引導(dǎo)其對“集合”數(shù)學(xué)概念進(jìn)行總結(jié)，激發(fā)復(fù)習(xí)學(xué)習(xí)興趣，從而讓學(xué)生圍繞集合概念為輔助，針對集合相關(guān)內(nèi)容進(jìn)行復(fù)習(xí)學(xué)習(xí)延伸，如集合的性質(zhì)、集合和元素之間的關(guān)系、集合的表示方法等。在有序問題引導(dǎo)中，打開思維的空間，提高概念復(fù)習(xí)學(xué)習(xí)效果。

2.設(shè)計(jì)生活問題，培養(yǎng)數(shù)學(xué)抽象素養(yǎng)，增強(qiáng)復(fù)習(xí)學(xué)習(xí)能力

在高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)中，很多概念是抽象的，需要學(xué)生通過大腦進(jìn)行想象。基于此，為提高復(fù)習(xí)學(xué)習(xí)能力，培養(yǎng)數(shù)學(xué)抽象核心素養(yǎng)，可以設(shè)計(jì)生活問題，以生活實(shí)際為載體，圍繞生活素材設(shè)計(jì)問題情境，增強(qiáng)學(xué)習(xí)體驗(yàn)感，讓復(fù)習(xí)更加高效。例如，在教學(xué)《平面向量的概念》數(shù)學(xué)內(nèi)容時，重點(diǎn)是理解向量的概念，理解平面向量的含義，能夠利用有向線段研究向量過程，發(fā)展數(shù)形思維。在教學(xué)的時候可以設(shè)計(jì)以下生活問題為輔助，如：

師：同學(xué)們，在語文學(xué)習(xí)中，我們聽到過南轅北轍的故事，你還記得最后的結(jié)果，和導(dǎo)致結(jié)果的原因嗎？

圍繞生活中的小故事為入手點(diǎn)，設(shè)計(jì)以下問題，引導(dǎo)其進(jìn)行探索分析：

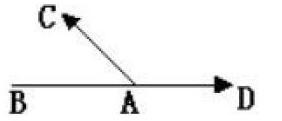
問題：如圖，在同一時刻，有一只老鼠由A向西北方向的C處逃竄，小貓正由B向正東方向的D處追，你覺得貓是否能抓到老鼠呢？

思考：在這一問題中，有哪些量，這些量共同的特征是什么？

在生活問題引導(dǎo)中，引出向量的概念“有大小又有方向的量叫向量”提高復(fù)習(xí)學(xué)習(xí)能力，培養(yǎng)科學(xué)的探索精神，在復(fù)習(xí)理解向量概念的基礎(chǔ)上，引導(dǎo)學(xué)生進(jìn)行復(fù)習(xí)練習(xí)，如：

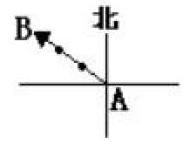
小船由A地向西北方向航行15海里到達(dá)B地，小船的位移如何表示？

從生活問題入手，提高概念復(fù)習(xí)學(xué)習(xí)興趣，使其認(rèn)識到數(shù)學(xué)概念在實(shí)際生活中的應(yīng)用，使得抽象概念得到直觀展示，讓問題引導(dǎo)更加具有目的性，實(shí)現(xiàn)學(xué)以致用。

3.設(shè)計(jì)深度問題，探索概念發(fā)展特點(diǎn)，提高復(fù)習(xí)教學(xué)質(zhì)量

提高復(fù)習(xí)教學(xué)質(zhì)量，認(rèn)識概念發(fā)展特點(diǎn)，在進(jìn)行問題引導(dǎo)的時候，要注意設(shè)計(jì)有深度的問題，促進(jìn)其深度學(xué)習(xí)，從而發(fā)揮問題引導(dǎo)的教學(xué)價值，提高數(shù)學(xué)概念復(fù)習(xí)教學(xué)效果。通過問題引導(dǎo)，培養(yǎng)良好的思考學(xué)習(xí)習(xí)慣，使其能夠?qū)?shù)學(xué)問題、數(shù)學(xué)概念進(jìn)行深入學(xué)習(xí)探究。例如，在復(fù)習(xí)《函數(shù)的概念及其表示》數(shù)學(xué)內(nèi)容時，在教學(xué)的時候，可以聯(lián)系初中函數(shù)概念知識點(diǎn)為復(fù)習(xí)教學(xué)前提，如：

師：同學(xué)們，在初中我們就已經(jīng)接觸函數(shù)知識了，那么初中學(xué)過哪些函數(shù)，它們的定義域、值域、對應(yīng)法則分別是什么呢？

在回憶的基礎(chǔ)上，揭示導(dǎo)入高中函數(shù)的概念，讓學(xué)生對以下能夠表示函數(shù)關(guān)系的進(jìn)行判斷分析如：

在辨析函數(shù)關(guān)系的基礎(chǔ)上，復(fù)習(xí)函數(shù)概念，引導(dǎo)其思考分析：

①確定函數(shù)的要素有哪些？

②函數(shù)有哪些共同特征？

在深度問題引導(dǎo)的前提下，探索函數(shù)概念發(fā)展特點(diǎn)，提高復(fù)習(xí)教學(xué)質(zhì)量，從而引導(dǎo)學(xué)生依據(jù)函數(shù)概念定義，進(jìn)行復(fù)習(xí)探索，在概念復(fù)習(xí)的基礎(chǔ)上，開展“我是火眼金睛”的判斷活動，讓學(xué)生進(jìn)行問題搶答如：

判斷下列函數(shù)中哪個與函數(shù)y=x是同一個函數(shù)？

讓學(xué)生依據(jù)對函數(shù)概念的復(fù)習(xí)理解，進(jìn)行問題判斷解析，在活動開展的過程中，提高復(fù)習(xí)學(xué)習(xí)效率，在深度問題引導(dǎo)中，促進(jìn)對概念的掌握和消化。

4.設(shè)計(jì)系統(tǒng)問題，揭示數(shù)學(xué)概念本質(zhì)，完善復(fù)習(xí)學(xué)習(xí)計(jì)劃

對于高考而言，在考察某一知識點(diǎn)的時候，并不是單單針對一個難點(diǎn)、重點(diǎn)進(jìn)行的考察分析，需要學(xué)生結(jié)合多個知識板塊內(nèi)容進(jìn)行分析探索。在概念復(fù)習(xí)的時候，為揭示數(shù)學(xué)概念本質(zhì)，完善復(fù)習(xí)學(xué)習(xí)計(jì)劃，教師要設(shè)計(jì)系統(tǒng)問題，從多角度進(jìn)行問題引導(dǎo)，促進(jìn)思考分析，提高概念理解和掌握。例如，在教學(xué)《三角函數(shù)的概念》數(shù)學(xué)復(fù)習(xí)內(nèi)容的時候，可以設(shè)計(jì)以下系統(tǒng)的復(fù)習(xí)問題，如：

①在初中已經(jīng)學(xué)過銳角三角函數(shù)，思考以下問題。

②這些與∠A有關(guān)的比值為什么稱它們?yōu)楹瘮?shù)，這些三角函數(shù)值與直角三角形的大小有關(guān)系嗎？

思考：角α的三角函數(shù)是否受終邊上的點(diǎn)P的位置的影響？以上幾個三角函數(shù)的自變量是什么？x還是y？r還是角α？對應(yīng)法則又是什么？

通過回憶初中銳角三角函數(shù)知識，帶入高中所學(xué)的任意角三角函數(shù)，在銳角和任意角擴(kuò)展的基礎(chǔ)上，提高概念復(fù)習(xí)的廣度，使之學(xué)習(xí)更加系統(tǒng)化，完成從三角形到坐標(biāo)系的轉(zhuǎn)化，從而使之明白銳角三角函數(shù)和任意角三角函數(shù)之間的聯(lián)系，體會兩個定義的相關(guān)性，讓學(xué)生在復(fù)習(xí)的時候，能夠多角度、全面的制定復(fù)習(xí)學(xué)習(xí)計(jì)劃。

四、結(jié)語

基于問題引導(dǎo)的高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)，教師要遵從問題設(shè)計(jì)的原則，認(rèn)識問題引導(dǎo)在高中數(shù)學(xué)概念教學(xué)中應(yīng)用的價值。通過設(shè)計(jì)有序問題、生活問題、深度問題、系統(tǒng)問題等，提高復(fù)習(xí)學(xué)習(xí)興趣，強(qiáng)化高中概念復(fù)習(xí)教學(xué)效果。

[參考文獻(xiàn)]

[1]印曉天.基于問題引導(dǎo)的高中數(shù)學(xué)概念深度學(xué)習(xí)的探索[J].中學(xué)數(shù)學(xué)，2020（13）：91-92.

[2]陳飛飛.淺談問題引導(dǎo)背景下的高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)[J].數(shù)學(xué)教學(xué)通訊，2020（21）：25-26.

[3]糜英建.探究概念本質(zhì)，促進(jìn)概念生成——高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)策略分析[J].數(shù)學(xué)教學(xué)通訊，2020（18）：27-28.

[4]鄭紅衛(wèi).突出概念，提高效率——對當(dāng)下高中數(shù)學(xué)概念復(fù)習(xí)教學(xué)的反思[J].數(shù)學(xué)學(xué)習(xí)與研究，2020（09）：29.

注：本文是增城區(qū)教育科學(xué)“十三五”規(guī)劃2019年度課題《“以問題為支架”的高三數(shù)學(xué)復(fù)習(xí)課有效性研究》課題編號：zc2019029的研究成果。

（作者單位：廣州市增城區(qū)高級中學(xué)，廣東 廣州 510000）