引導學生建構數學模型的教學策略

張小英

[摘 要]建構數學模型是一個數學抽象和數學概括的過程。結合“乘法分配律”一課的教學，探討如何借助幾何直觀及變式練習，引導學生感知、抽象并內化“乘法分配律”模型，以此提升學生的數學素養。

[關鍵詞]數學模型;乘法分配律;建構策略

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2021）35-0063-02

數學課程標準特別強調，在引導學生進行數學學習的過程中，必然要經歷對實際問題進行抽象的過程，使其可以自主建構數學模型，并完成解釋和應用。對學生來說，數學建模必然是一個自主化的過程，但是當前的教學實踐未對建模過程展開深入探究，所以很多學生對數學建模的理解普遍停留在表面，難以準確把握其內涵。

“乘法分配律”是小學數學教學的難點所在，在具體教學過程中，教師需要結合記憶以及反復的練習，引導學生深入探究，進而體會數學模型的建構過程。這一點非常關鍵，不僅有助于學生理解乘法的意義，還能夠讓學生對乘法分配律的成因展開深度思考，幫助學生完成對數學模型的建構，高效且透徹地理解其內涵。

一、借助幾何直觀，感知“乘法分配律”模型

雖然引入學生比較熟悉的生活問題，可以拉近學生和乘法分配律之間的距離，但是想要實現成功的教學，不僅要揭示其現實意義，還要使學生透徹地理解其數學意義。而在教學過程中引入幾何直觀，可使學生對乘法分配律的數學模型形成更深刻的感知。

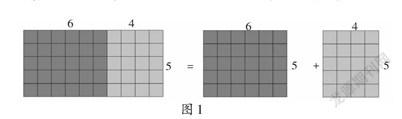
首先向學生呈現教材中的主題圖，然后設計數學問題：在給廚房貼瓷磚的過程中，如果左面墻壁每排能夠貼5塊，總計貼4排，右面墻壁每排可以貼5塊，總計貼6排，請問一共需要多少塊瓷磚？

在解答這一問題之前，要求學生先畫圖，再列式。學生很快列出了兩道不同的算式：（6+4）×5=50（塊）;6×5+4×5=50（塊）。

師：大家先認真觀察大屏幕所給出的圖形（如圖1），然后和同桌探討為什么這兩個算式是相等的。

生：因為等號左邊代表的是10個5相加，而右邊代表的是6個5相加和4個5相加，因此這兩個算式相等。

在理解這一知識點時，學生自主聯系了之前學習過的長方形面積計算公式，可見，圖形能夠輔助學生理解算理。同時在學生進行表達時，教師還要提高他們數學語言的表述能力，為接下來乘法分配率的提煉奠定基礎。

數學這門學科探討的是空間形式和數量之間的關系，數形之間保持著極其緊密的關聯。因此，在組織教學時，不僅要強調乘法的意義，還要引入數形結合，幫助學生建立豐富的表象認知，體會數與形之間的密切關聯，然后理解其本質含義。這樣才能夠為下一步數學模型的建構奠定良好的基礎。

二、引導數學概括，抽象“乘法分配律”模型

當學生對模型建立了初步的感知之后，可向其提供大量的類似材料，幫助學生豐富表象、感悟模型，并留足夠的思考空間，使學生可以通過具體的例子發現規律，然后使用規范的數學語言對其進行描述，完成對模型的抽象和建構。

1.引導數學觀察，探究算式規律

首先給出兩個算式（55+38）×2=55×2+38×2和（6+4）×3=6×3+4×3，要求學生觀察等式兩邊，找出規律，然后使用規范的數學語言表達。學生基于現有的認知水平，已經能夠做出相對準確的表述：等式左右兩邊相等，左邊是兩數之和與另一個數相乘，右邊是兩個加數分別與乘數相乘，然后再相加。

2.引導舉例驗證，歸納算式規律

師：這個規律可以適用于任何地方嗎？是否可以舉出一些實例？

生1：例如（3+9）×22=3×22+9×22。

師：在這個例子中，等式的左右兩邊分別代表什么？

生1：左邊是12個22的和，右邊是3個22和9個22的和。

生2：又如（2+7）×3=2×3+7×3。

師：請你也解釋一下。

生2：左邊是9個3的和，右邊是2個3和7個3的和。

……

師：通過大家所舉的例子，我們可以發現，根據計算結果，能夠證明這個計算規律成立，這個規律叫作“乘法分配率”。如果讓你介紹這個規律，你會怎樣表達？

生3：兩數相加的和與另一個數相乘，所得的結果與這兩個數分別與乘數相乘之后再相加的結果相等。

之后組織學生思考，完成模型（▲+■）×●=？的建構。學生得出：（▲+■）×●=▲×●+■×●。針對學生的回答，教師先表示肯定，然后再對具體的規律進行總結歸納。

3.引導交流總結，抽象數學模型

師：我們可以使用更簡單的數學語言來呈現這個規律：（a+b）×c=a×c+b×c。

所謂數學表象，就是根據所呈現的客觀事物，以及結構或者形式，對其進行概括或者描述，由此形成觀念性表象，如圖式。通過這一方式，可以幫助學生對計算規律形成初步感知，在經過對比、觀察以及分析之后，總結規律，嘗試描述、表達，然后再對規律進行抽象，形成數學模型。為了確保這一環節順利開展，需要教師在建模時引導學生仔細觀察數學符號，進而完成模型建構以及相對規范的語言表達。

三、借助變式練習，內化“乘法分配律”模型

在應用乘法分配律的過程中，很多學生出現了理解以及應用困難，他們能夠理解 a×c+b×c=（a + b）×c，但是逆向運用就出現了困難，既不能形成直觀的感知，也難以實現意識層面的深度理解。為此，需要運用合理的方式引導學生逆向思考問題。一方面要加強練習，使學生理解乘法的意義;另一方面，需要完成對模型結構的內化，幫助學生深化認知，加強應用。

1.借助對比練習，強化模型認知

實際應用過程中，學生經常會出現錯用的情況，如所給出的算式并不需要應用乘法分配律，卻被學生錯誤地使用。特別是在一些簡化運算中，有些學生會忽視“因數相同”這樣一個非常關鍵的條件。針對學生的這一易錯點，可給出兩道算式：（1）47×88+53×88;（2）47×88+53×89。

解題之前，先要求學生對比這兩個算式，然后展開細致觀察，找出二者的異同，然后再和同桌展開探討。學生發現這兩道算式都是求兩個乘積之和，但是算式（1）中有一個因數相同，算式（2）沒有相同的因數。根據學生的這一發現，要求他們對照乘法分配律，了解只有算式（1）才適用這一法則。這樣的方式能夠幫助學生深化認知，感受其中的關鍵性條件。

很多學生還會將乘法分配律與乘法結合律相混淆，所以需要在練習中增加對比環節：通過多個題組，引導學生準確把握不同的規律以及特點。例如，（40+4）×25和（40×4）×25、25×125×25×8和25×125+25×8。在練習之前，可以輔以引導式提問：這幾組算式具有怎樣的特征？存在怎樣的區別？分別需要運用哪個運算規律？借助這一運算規律，是否可以真正簡化運算過程？這么計算的原因是什么？讓學生通過對比，清晰地把握不同法則各自的特征以及應用條件，深化學生的理解，強化學生的認知和記憶。

2.借助逆向練習，內化數學模型

在教學乘法分配律的過程中，需要教師給出豐富的感性材料，使學生展開有目的、有順序的觀察，并通過合理的對比和逆向練習，內化數學模型。為此，教師可提供兩組練習：（1）99×38+38;（2）46×38+54×39。

學生剛接觸這兩道題時，都認為不能使用乘法分配律解題，但通過仔細觀察，就能夠發現這兩道題很有特點，可以對其進行變式，之后再應用對應法則。例如算式（1），可以將38改寫為38×1，這樣就能夠成功地利用之前所學習的舊知，即某個數與1相乘，這個數不變。在引入這一知識點之后，不僅有助于提高學生的解題能力，還能夠就此深化他們的認知。對于算式（2），通過觀察可以發現，其中有兩個乘數相加之后能夠得到100，對此學生就會思考：在不存在相同因數的情況下，究竟應該怎樣變式才能使用乘法分配律對其進行簡化呢？教師引導學生關注乘數39，對比前一組數字中的38，兩者相差1，將39改寫為38+1，就可以解決這一問題。在上述兩道題中都使用了乘法分配率，一次為順向、一次為逆向，通過這樣解題，有助于深化學生對知識點的認知，有效訓練其思維的靈活性，提高其解題能力，使其樹立解題自信，并從內心生發濃厚的數學學習熱情。

總之，在學習乘法分配律的過程中，既要充分鏈接學生的生活經驗，使學生可以完成對數學模型的提煉以及建構，還要輔以數形結合，幫助其理解深化認知，并為日后的深入學習奠定良好的基礎。

（責編 羅 艷）