培養初中生數學思維廣闊性的策略研究

肖文記

摘? 要：初中生數學思維廣闊性的培養，要設置開放的問題情境，讓學生從不同角度去探究，形成多樣結論;要重視歸納概括，從局部到整體，從特殊到一般，總結方法;要多元聯系，在不同知識領域中探究，形成各自解法;在開放、概括和關聯中創新方法，發展思維的廣闊性。

關鍵詞：數學思維;思維廣闊性;開放探究;一般概括;多元聯系

數學思維的廣闊性，要求人們在思維過程中，充分運用積累的知識和經驗，舉一反三，觸類旁通，進行有效的思維。在思維過程中，教師要引導學生從基本概念、基本原理出發，對數學對象及數學對象之間的關系開展多角度、多層次的探究活動，通過歸納、類比、演繹等各種思維方式發現概念的多元聯系，深化對數學問題的認識，在探尋問題的不同解決方法中拓寬思路，將思維引向廣闊。

一、在開放探究中發展思維的廣闊性

初中數學題目大多數是定向問題，學生根據問題展開定向分析，思維局限在狹小的空間內。要打破這種局面，就要適當進行開放探究，鼓勵不同的學生呈現不同的思維，在交流中展開思維的碰撞，取長補短，讓思維從狹窄到廣闊。

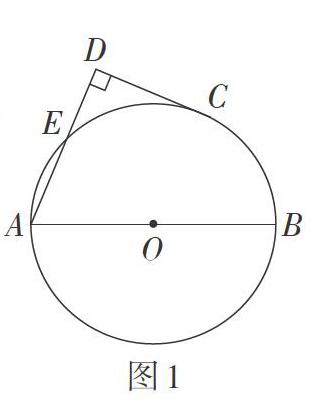
例如，將人教版《義務教育教科書·數學》九年級上冊習題中的問題去掉，只呈現條件。如圖1，AB是[⊙O]的直徑，C為[⊙O]上一點，AD和過點C的切線互相垂直，垂足為點D。在中考第一輪復習時，以問題串的形式呈現給學生。

問題1：根據題目條件，添加一條輔助線，你可以得到什么結論？

問題2：根據題目條件，添加兩條輔助線，你可以得到什么結論？

問題3：若DE = 2，DC = 4，求圓的半徑。

問題4：除了可以求出圓的半徑，你還能求出其他線段的長度嗎？或者求出哪些角度的三角函數值？嘗試算一算。

問題5：若[sin∠BAC=35]，你能求出[tan∠BDC]的值嗎？

問題6：為什么可以進行如此多的線段轉化，題目條件給了我們什么幫助？根據對這道題的探究，你能總結出解決這類問題的基本結論嗎？

此處采用開放問答式教學，教師提問，引導學生思考，有些問題沒有固定答案，有些問題沒有方向。學生根據已有的知識和經驗得出不同結論，從全等到相似，再到三角函數，實現了多角度、多層次的拓展，由點到線，由線到面，形成圖形的全局。

二、在一般概括中發展思維的廣闊性

思維是人腦對客觀事物的間接的、概括的反映。概括是思維的特性，教師要充分運用積累的知識和經驗，舉一反三，觸類旁通，進行一般結論的概括，實現有效思維。

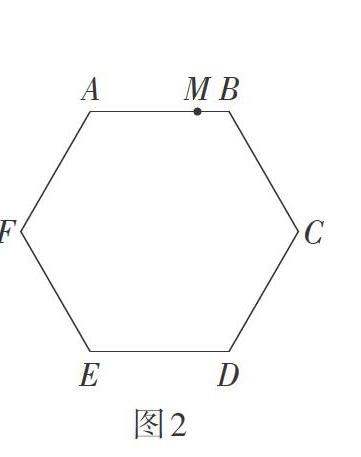
例如，無刻度直尺作圖中對正六邊形的探究。如圖2，已知正六邊形ABCDEF，試僅用無刻度的直尺按要求畫圖，畫圖過程用虛線表示，畫圖結果用實線表示，按步驟完成下列問題，并簡要說明畫法及原理。

問題1：畫出正六邊形ABCDEF的中心O。

問題2：畫出正六邊形任意一邊的中點。

問題3：圖2中M為AB上一點，以點B為端點在正六邊形的邊上畫線段BN = BM。

問題4：將問題3中的方法運用到以點C為端點在正六邊形的邊上畫線段CG = BM。

問題5：將問題3中的方法運用到其他頂點上。

問題6：將問題3中的方法運用到在六條邊的延長線上，取線段與BM相等。

此處將問題延伸，將方法延續，將一個點的對稱方法類比到六個點的作法，將邊上的作法遷移到線段的延長線上，從特例開始，循序漸進，最后歸納了一般化的結論，一般化的結論又可以推廣到n邊形的研究，學生的思路打開，思維引向廣闊。

三、在多元聯系中發展思維的廣闊性

對問題的探究要善于多方探索，這樣不僅能研究問題本身，聯系相關的其他問題，還能跨領域關聯，在多元聯系中探究不同的解法，發展思維的廣闊性。

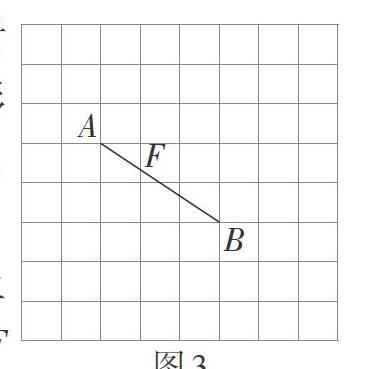
例如，無刻度直尺作圖中對作垂直的探究。如圖3，在正方形網格中，線段AB交網格線于點F，過點F作FG⊥AB。

方法1：以AB為邊，在AB上方作正方形ABCD，取CD邊上F的對應點G，連接FG即可。

方法2：將AB邊下移三個單位長度，再左移2個單位長度，找到F的對應點G，連接FG即可。

方法4：將點F下移1.5個單位長度，再左移1個單位長度，得到點G，連接FG即可。

此處由此及彼，橫向關聯，不斷轉化，從幾何、平移、解析、相似四個不同角度進行了探究，從一般到特殊，數形結合，呈現了不同領域不同的精彩解法，讓學生對作垂直的方法有了全面的認識，讓思維從單一走向多元。

從以上各例可以看出，教師在解題與講題時，要擺脫只為解題而解題的束縛，要以題為載體發展學生思維，著眼思維的廣闊性。通過設置開放的情境與問題，讓不同的學生有不同層次的思考;通過一題多變進行廣泛研究;通過一法多用，展開推廣，在用中升華;從特殊到一般，展開關聯，多元聯系，積極鼓勵學生勤于思考，敢于求異，全面促進學生思維廣闊性的發展。

參考文獻：

[1]曹才翰，章建躍. 中學數學教學概論[M]. 北京：北京師范大學出版社，2008.