淺談“尺規作圖”的關鍵點教學

曾立萱

摘要：尺規作圖是全國中考的高頻考點，考法新穎多變。不僅要掌握基本的尺規作圖方法，還要靈活運用幾何圖形的性質，將題目信息轉化一次或多次，得出要作的基本尺規作圖。近三年福建省中考尺規作圖是以解答題的形式呈現的，既要求尺規作圖，還要求幾何證明、幾何計算。所以要拿到本題的滿分，就要教師“高屋建瓴”，準確把握尺規作圖的關鍵點教學。

關鍵詞：尺規作圖；轉化；教學關鍵點；動手操作；邏輯推理；數學建模

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2021）19-0127

初中數學平面幾何中，對圖形的學習有四個不同層次：看圖、析圖、畫圖、用直尺與圓規作圖。尺規作圖的作圖工具只能是直尺（沒有刻度）與圓規。與尺規作圖相關的題目主要在于訓練學生的作圖分析、合情說明作圖過程、規范地用直尺與圓規操作。縱觀近幾年福建中考數學試題發現：作圖題已由以往形式上的單一而轉向多樣型和復合型，突出考查學生對“尺規作圖”的理解、操作、綜合應用能力。《尺規作圖》以它特有的魅力，備受命題者青睞。

一、原題呈現

（2020年福建中考數學卷第23題）如圖，已知點C是線段AB外一點。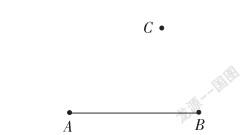

（1）求作四邊形ABCD，使CD∥AB且CD=2AB

（要求：尺規作圖，不寫作法，保留作圖痕跡）

（2）在（1）的四邊形ABCD中，AC與BD相交于點P，

AB、CD的中點分別為M、N，求證：M、P、N三點共線。

二、作法賞析

1.作一個角等于已知角

解法1：如圖1，利用基本作圖作∠DCM=∠ABC；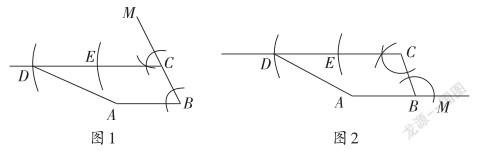

解法2：如圖2，利用基本作圖作∠DCB=∠CBM；

【點評1】這兩種畫法是大部分考生的主流作法，也是最容易想到的作圖方法，作法1利用“同位角相等，可得兩直線平行”，再作CD=2AB。作法2利用“內錯角相等得兩直線平行”。

在圖1中，若連結AE，可得平行四邊形ABCE。由此還可以想道：先以△ABC的AC邊為對角線作平行四邊形ABCE；再在射線CE上截取ED=CE。問題轉化為：已知三點A、B、C不在同一條直線上，求作：點E，使得四邊形ABCE是平行四邊形.

2.作特殊圖形：平行四邊形

解法3：如圖3，利用SSS作△ABC的全等三角形△CAE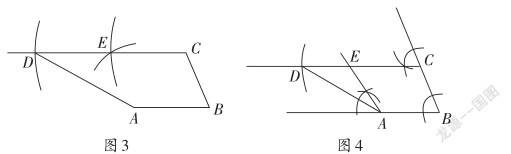

解法4：如圖4，通過“作一個角等于已知角”，得CE∥AB，AE∥BC，得平行四邊形ABCE。

作圖依據是“經過直線外一點有且只有一條直線與已知直線平行”。

解法5：如圖5，過點A作BC的平行線AE；再在射線AE上截取AE=BC，得平行四邊形ABCE。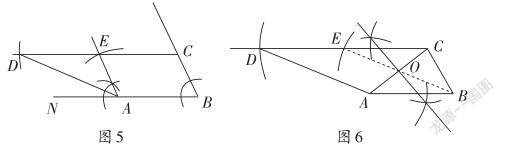

解法6：如圖6，作AC的中垂線，再作點B關于點O的對稱點E，得平行四邊形ABCE。

解法7：如圖7，先作線段BE=2AB；再利用“有兩組對邊分別相等的四邊形是平行四邊形”，得平行四邊形EBCD。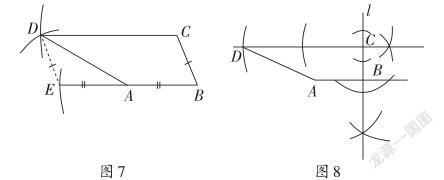

【點評2】以上解法3到解法7，共同之處是“作特殊圖形——平行四邊形”。在解題時需運用“數學的化歸與轉化的思想”。把問題進行轉化，實現從“組合作圖”到“基本作圖”的分解與思想轉化。作圖中應注意“作一個線段等于已知線段”“作一個角等于已知角”“作已知線段的垂直平分線”及“交軌法”確定點E的位置。由于平行四邊形的多種不同判定方法，所以產生了尺規作圖的“一題多解”。

這道中考題在考查尺規作圖的同時綜合考查了平行四邊形的多種證明方法，考核了學生的幾何推理能力。所以在平時教學中依據隱藏的條件，作三角形、平行四邊形、矩形、正方形要多加以變式訓練。

3.作垂線

我們知道“在同一個平面內，垂直于同一條直線的兩條直線互相平行”，所以可以把“過點C作AB的平行線”轉化為作垂線。

解法8：如圖8，先過點C作直線l⊥AB；再過點C作直線m⊥l，則直線m∥直線AB；最后再作CD=2AB。

【點評3】這種解法也是大多數學生會想到的。利用“過一點有且只有一條直線與已知直線垂線”，作兩次垂線，從而這兩條垂線互相平行。第一次“過直線AB外一點C作直線AB的垂線”；第二次“作已知直線l上的點C作直線l的垂線。

4.構造法

解法9：構造三角形的中位線

如圖9，先在射線CB上截取BE=BC，再在射線EA上截取AD= AE，連結CD。

則由作圖可知AB是△DCE的中位線，從而DC∥AB且DC= 2AB。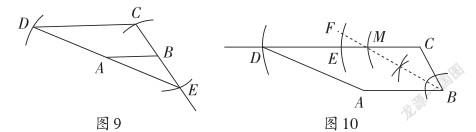

解法10：構造“角平分線+等腰三角形”模型，推得平行線

如圖10，作BF平分∠ABC；以點C為圓心，以CB為半徑畫弧，交射線BF于點M，可得CM∥AB；在射線CM上依次截取CE=ED= AB。

【點評4】構造法主要是用到常見的幾何模型。方法9構圖巧妙，作圖簡單，整體轉化；方法10轉化程度高，學生在考場限時考試中較難想到。教師在平時教學中要“一題多解”，從不同的角度思考問題，培養學生發現幾何模型的能力、幾何直觀能力、發散思維能力。

三、關于尺規作圖教學關鍵點的幾點思考及教學建議

對于2020年中考數學第23題，第（1）步是作圖題，第（2）步是“三點共線”幾何證明問題（可以用“相似法”“同一法”“解析法”加以解決，這里不展開敘述）。筆者發現近三年福建中考的尺規作圖都是放在解答題的位置，所占分值有所增加，這個現象引起筆者的思考。

1.高度重視尺規作圖教學的意義

尺規作圖是初中生必須掌握的作圖技能，在教學過程中可以培養學生良好的作圖習慣、作圖與幾何推理有機結合的能力，所以在初中需高度重視尺規作圖。

例如：華東師大版七上《9.1三角形中的重要線段》的教學中，就可以要求學生用尺規作圖作出三角形中線、角平分線、高線，從而發現三角形的重心、內心、垂心；在八上《全等三角形》這一章，探索兩個三角形全等的條件，也是由尺規作圖得到兩個三角形，再由“疊合法”“歸納法”得出SSS、SAS等判定方法。

同時，通過向學生介紹尺規作圖三大難題、結合軟件幾何畫板，大大激發學生探究的興趣。在高中學習中要求掌握圓錐曲線切線的尺規作圖，用到了“交軌”原理。在作圖中，學生會體會到幾何的美麗，對學生今后從事美術設計、機械制造等精確繪圖等有很大的啟發與引領作用。

2.準確把握尺規作圖的教學要求

（1）教學核心內容

①合理表述作圖過程；②明確每一步作圖的步驟與依據；③規范作圖。

（2）教學基本題型

落實好以下幾種類型的尺規作圖：①五種基本作圖；②作三角形或四邊形；③作三角形的內切圓或外接圓；④作三角形的全等或相似；⑤作線段的三等分點；⑥作已知點關于已知直線的對稱點；⑦作圓的內接正方形，圓的內接正六邊形等；⑧利用基本作圖解決生活實際問題。

（3）作圖關鍵點

把“組合作圖”轉化為“基本作圖”。方法是：先畫目標圖形的草圖；再分析目標圖形的幾何性質，從而得到作圖的整體思路；最后按基本作圖的步驟規范操作。

例：如圖，已知△ABC中，∠ACB=90°。

①求作：在邊AB上找一點O，以點O為圓心作⊙O，使得⊙O經過點A且與邊BC相切.

②若AC=8，AB=10，求所作的⊙O的周長。

解析①：如圖所示，先作∠BAC的角平分線AD；再作線段AD的垂直平分線，交AB邊于點O；最后以點O為圓心，OA為半徑作圓O，則圓O為所求。

解析②：用相似三角形對應邊成比例可求半徑（請大家試一試）

在這個例題教學中，可以訓練學生：目標圖形的轉化、分解、具體作圖時所用到的幾何推理依據，通過尺規作圖促進學生的幾何思維。

3.在尺規作圖中加強數學思想方法的滲透

尺規作圖中所涉及的數學思想主要是：（1）分類討論；（2）化歸與轉化。

在華師大版《義務教育教科書.數學》九年級下冊“27.2.1點與圓的位置關系”中探討《幾點可以確定一個圓》。主要考查“作已知線段的垂直平分線”，但在分析中滲透分類討論與交軌法定點。教師要領會教材的安排意圖，在這一系列變化中挖掘更深的內涵，滲透數學思想。

又如：已知圓O、點P在⊙O外，用直尺和圓規過點P作⊙O的切線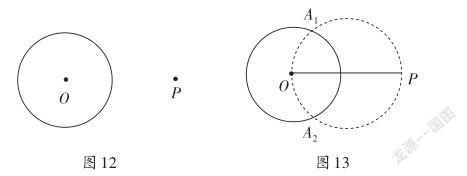

解析：若切點是點A，則必有OA⊥AP于點A，即∠OAP=90°，問題轉化為：尋找以OP為斜邊的直角三角形的直角頂點A的軌跡。故作“以線段OP為直徑作圓”，點A是所作的圓與圓O的交點（有2個）

4.尺規作圖的關鍵點教學策略

（1）構建尺規作圖的思考方法：分析問題、轉化結論。

（2）注意原題的拓展與歸納，知識的遷移與聯系。

（3）數學建模，學以致用。

（4）回歸中考試題，提升解題能力。

四、結束語

“數學課程要讓學生獲得適應社會的知識與技能”。目前尺規作圖的功能主要體現在實踐應用、樣板圖紙的設計及美術圖案設計方面。在教學取材方面，可以增加生活方面圖案，讓學生用尺規作圖完成，提高實踐操作能力。同時，教師還可以介紹flash、CAD、Photoshop等專業畫圖軟件，激發學生的探索欲望，為將來進行專業學習奠定基礎。

參考文獻：

[1]劉芳.對尺規作圖教學的三個思考[J].中學數學雜志，2009（10）.

[2]孫振國.淺談尺規作圖之變遷[J].中小學數學（初中版），2010（3）.

[3]梅列亭.尺規作圖走進生活[J].初中生學習指導，2018（10）.

[4]蔣凱.尺規作圖教學用力點在哪兒——由尺規作圖的作業批閱說起[J].中學數學，2019（22）.

（作者單位：福建省泉州市第七中學金山校區362000）