基于數(shù)學(xué)核心素養(yǎng)的高中數(shù)學(xué)單元教學(xué)設(shè)計的實踐研究
黎明
【摘要】為了有效培養(yǎng)高中學(xué)生的數(shù)學(xué)核心素養(yǎng),本文通過立足于數(shù)學(xué)核心素養(yǎng)來深入分析數(shù)學(xué)單元教學(xué)設(shè)計的實踐策略,有效提升高中學(xué)生的數(shù)學(xué)水平。
【關(guān)鍵詞】核心素養(yǎng);高中數(shù)學(xué);單元教學(xué)
在當前高中教育深化改革的背景下,教學(xué)大綱對學(xué)生的學(xué)習(xí)要求不斷提高,所以便需要高中老師創(chuàng)新教學(xué)策略。通過將高中數(shù)學(xué)課程教學(xué)與創(chuàng)新數(shù)學(xué)課堂教學(xué)進行對比分析,在高中數(shù)學(xué)課堂的教學(xué)過程中不僅僅只是向?qū)W生傳授教學(xué)方法,還需要指導(dǎo)學(xué)生建立起完善的知識體系,注重學(xué)生的人格培養(yǎng),有效提升學(xué)生的數(shù)學(xué)核心素養(yǎng)。本文在研究中以“平面向量”這個單元內(nèi)容為例進行分析。
一、基于數(shù)學(xué)核心素養(yǎng),選定合理的單元內(nèi)容
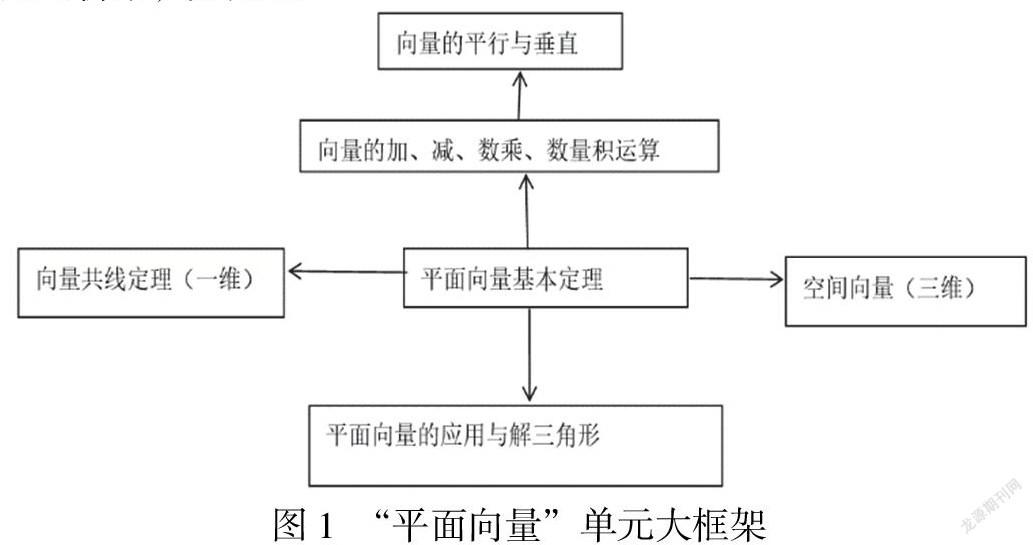
在基于數(shù)學(xué)核心素養(yǎng)的高中數(shù)學(xué)單元教學(xué)設(shè)計中,以“平面向量”這個單元的內(nèi)容為例進行分析,理清各個知識點自身的邏輯順序,并需要緊密結(jié)合各個知識點發(fā)展的邏輯順序和思路來構(gòu)建起本單元的框架。其中,這個單元的核心內(nèi)容就是平面向量的基本定理,具體分析了平面內(nèi)的各個向量與有序?qū)崝?shù)所構(gòu)成的一一對應(yīng)的關(guān)系,讓向量間的運算逐步轉(zhuǎn)化成為代數(shù)運算。這樣當學(xué)生在學(xué)習(xí)完了向量的相關(guān)知識點之后,便可以在正弦定理、兩角和與差的正余弦公式等三角問題的證明過程中應(yīng)用向量的相關(guān)知識,讓平面向量真正成為溝通幾何知識與代數(shù)、三角問題的重要橋梁,如圖1。
二、綜合梳理知識與核心素養(yǎng)的相關(guān)性,注重鍛煉學(xué)生的邏輯推理能力
在當前高中數(shù)學(xué)課程的教學(xué)過程中,大部分學(xué)生對于平面向量的概念知識點的認識還比較陌生,所以在學(xué)生初步接觸的時候則難以理解其內(nèi)涵。因此,作為高中數(shù)學(xué)老師,便可以結(jié)合數(shù)學(xué)課程中所蘊藏的各個知識點來指導(dǎo)學(xué)生進行觀察和類別,讓學(xué)生的認知里能夠逐步擺脫對具體事物和抽象的數(shù)學(xué)對象的認同,嚴格遵從數(shù)學(xué)知識點的規(guī)律,以此在思維里形成向量這個概念。
向量主要包括了大小和幾何兩個屬性,所以作為平面向量不僅有大小,而且也是有方向的量。因此,在對平面向量這個概念進行定義之后,則逐步出現(xiàn)了零向量和單位向量;在學(xué)習(xí)了向量的方向性之后則逐步出現(xiàn)了平行向量、共線向量和垂直向量。這樣向量在兼顧了兩者的屬性之后則出現(xiàn)了相等向量和相反向量兩個概念。其中,在學(xué)習(xí)這些向量的概念知識點的時候,應(yīng)該積極引領(lǐng)學(xué)生逐步從現(xiàn)實的事物中抽象出相關(guān)的要素,這樣才能夠真正形成抽象的數(shù)學(xué)概念。學(xué)生在這個概念知識點的學(xué)習(xí)過程中則能夠逐步形成良好的數(shù)學(xué)核心素養(yǎng)。
通過立足于數(shù)學(xué)運算的角度來進行分析,向量在本質(zhì)上既有幾何的性質(zhì),又有代數(shù)的屬性,所以我們在研究的過程中便主要是將運算及其遵循的運算規(guī)律、運算性質(zhì)作為重點。一般情況下的向量運算方式包括了向量的加法、向量的減法、向量的數(shù)乘、向量的數(shù)量積。這樣從總體情況上則主要分為了加、減、乘。同時,在對向量的運算性質(zhì)進行分析的之后發(fā)現(xiàn),向量的運算不僅僅只是繼承之前所學(xué)習(xí)的內(nèi)容,也是一種代數(shù)運算性質(zhì)的拓展。
當學(xué)生從邏輯推理的角度出發(fā)進行分析,以O(shè)作為原點則被稱之為是數(shù)軸,這樣平面向量基本定理便在二維空間內(nèi)將實數(shù)與數(shù)軸上的向量建立起對應(yīng)的關(guān)系,讓向量用數(shù)值來進行表示,并將其作為向量坐標化的重要依據(jù)。通過指導(dǎo)學(xué)生從平面向量的基本定理再到三維空間內(nèi)向量的基本定理來學(xué)習(xí),能夠有效鍛煉學(xué)生的數(shù)學(xué)能力,有效提升學(xué)生的數(shù)學(xué)核心素養(yǎng)。
三、分課時進行設(shè)計,形成單元教學(xué)方案
在基于數(shù)學(xué)核心素養(yǎng)的高中數(shù)學(xué)單元教學(xué)設(shè)計實踐中,當編制好各個單元和各個課時的教學(xué)目標之后,再以這個目標作為方向去開展教學(xué)。通常教學(xué)方案的設(shè)計應(yīng)該從前期的準備、單元和課時目標的實施來進行整體分析,注重課程教學(xué)內(nèi)容的結(jié)構(gòu)化和邏輯化,充分凸顯出每一節(jié)課程內(nèi)容的針對性和目的性,讓整個數(shù)學(xué)課程的教學(xué)內(nèi)容能夠更加的連貫起來,讓數(shù)學(xué)核心素養(yǎng)的內(nèi)容真正滲透到數(shù)學(xué)教學(xué)中,以此達到強化學(xué)生數(shù)學(xué)核心素養(yǎng)的目的。例如,在“函數(shù)的單調(diào)性設(shè)計”這節(jié)內(nèi)容的教學(xué)過程中,因跨越的章節(jié)較多,所以教師在設(shè)計課時的時候應(yīng)該細化到各個階段,即第一個階段的目標則是讓學(xué)生在學(xué)習(xí)單調(diào)性概念的基礎(chǔ)上從圖形表示出發(fā),指導(dǎo)學(xué)生建立起符號語言和單調(diào)性的概念,讓學(xué)生能夠結(jié)合具體的問題來證明函數(shù)的單調(diào)性;第二階段則是引導(dǎo)學(xué)生列舉出基本函數(shù)的例子,深入研究函數(shù)的單調(diào)性,讓學(xué)生的幾何直觀能力得到有效增強,促使學(xué)生真正掌握函數(shù)單調(diào)性的作用;第三階段則是指導(dǎo)學(xué)生結(jié)合方程零點和不等式的知識點,注重函數(shù)的單調(diào)性與它們之間的聯(lián)系分析;第四階段則是通過把握函數(shù)單調(diào)性與導(dǎo)數(shù)之間的聯(lián)系,讓學(xué)生真正懂得函數(shù)這個變量間關(guān)系的數(shù)學(xué)模型,逐步形成良好的數(shù)學(xué)建模思想,有效增強學(xué)生的數(shù)學(xué)核心素養(yǎng)。
總之,在新課程深化改革的背景下,在高中數(shù)學(xué)課堂教學(xué)過程中越來越注重學(xué)生的數(shù)學(xué)核心素養(yǎng)培養(yǎng)。因此,基于數(shù)學(xué)核心素養(yǎng)下的高中數(shù)學(xué)單元教學(xué)設(shè)計,需深入分析高中數(shù)學(xué)課程內(nèi)容,積極采取有效的措施來注重學(xué)生的核心素養(yǎng)培養(yǎng),以便讓學(xué)生能夠更好的成長。
參考文獻:
[1]周德明,楊學(xué)穎.基于核心素養(yǎng)培育的高中數(shù)學(xué)"單元教學(xué)設(shè)計"——以"距離問題"一課的"單元教學(xué)設(shè)計"為例[J].中學(xué)數(shù)學(xué)教學(xué),2020(2):10-12.
[2]李小奎,韓娟.基于數(shù)學(xué)核心素養(yǎng)的高中數(shù)學(xué)單元教學(xué)設(shè)計的實踐研究[J].科教文匯,2020,000(007):137-138.

