動態幾何：賦予 “空間觀念”以生長的力量

任超

【摘 要】“圖形與幾何”作為數學課程四大板塊內容之一，重點培養學生的空間觀念。但由于傳統教學軟件的局限性，教師在教學圖形與幾何板塊時往往因工具而掣肘。筆者以幾何畫板為依托，結合具體實例，探索討論動態幾何在教學過程中的應用，為教師更好地幫助學生發展空間觀念提供幫助。

【關鍵詞】動態幾何 幾何畫板 空間觀念

“數學是研究數量關系與空間形式的科學。”空間形式最主要的目標是發展空間能力。動態幾何讓圖形“動”起來，在“運動或變換”中來研究、揭示、學習圖形的性質，這樣一方面可以加深對圖形特征的本質認識、體驗幾何原理的生長過程;另一方面可以培育數學情感，促進邏輯推理能力和直觀想象的能力發展，實現空間素養的提升。

一、審視：“動態幾何”教學現狀

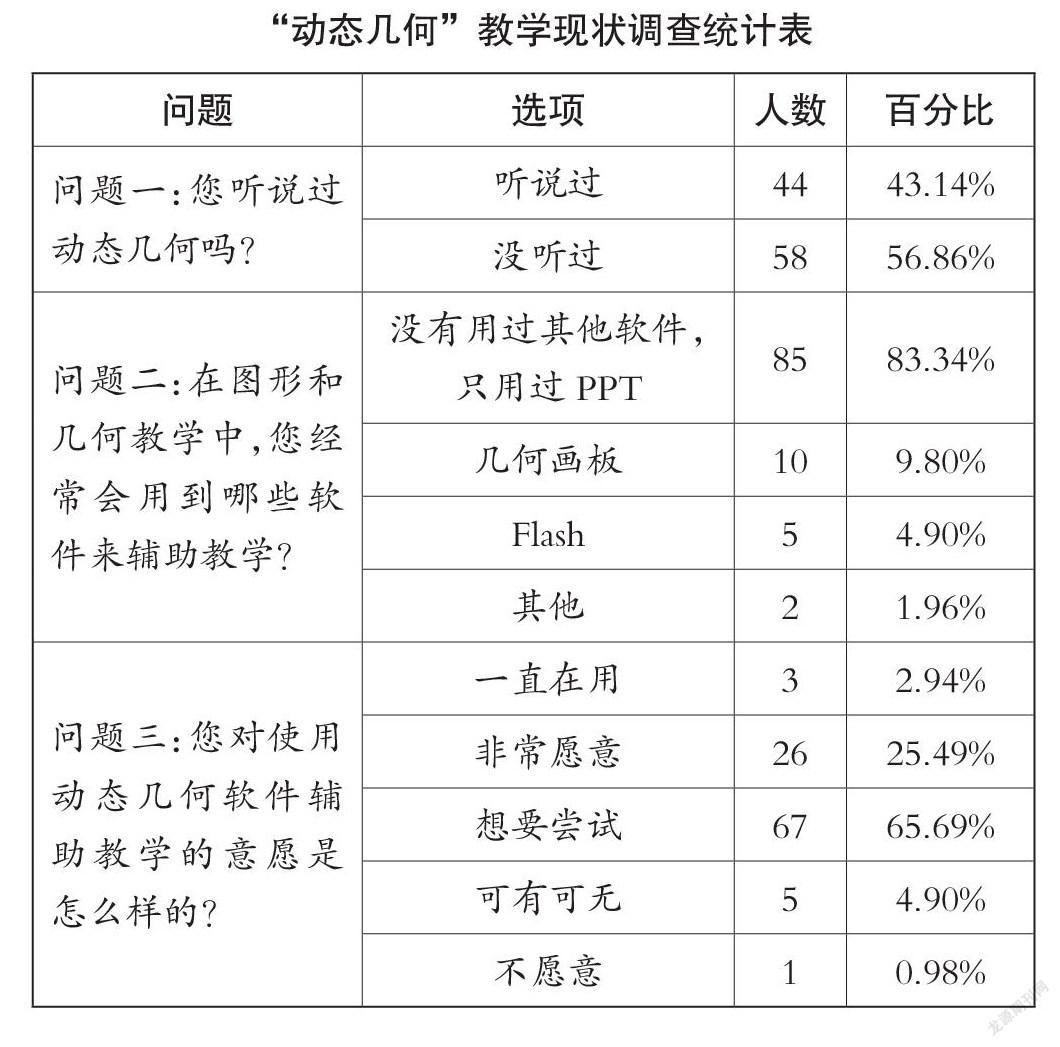
在小學數學課程中，“圖形與幾何”作為數學課程四大板塊內容之一，重點培養學生的空間觀念，在這個過程中就不得不提到一項與信息技術相關的策略——動態幾何。為了剖析目前小學數學“動態幾何”的教學現狀及教師對這一概念的認知，筆者通過“問卷”對所在地區的102位教師（其中21位低年級教師、29位中年級教師、52位高年級教師）進行了隨機調查，結果如下表。

通過調查統計表，我們發現：

（1）被調查的教師中，一半以上的教師對“動態幾何”這一概念不了解;

（2）在平時的圖形與幾何的教學過程中，大部分教師只采用演示文稿來進行教學，對于其他一些動態幾何的軟件運用很少。筆者通過與幾位被調查的教師談話發現，出現這種現象的原因大致有這幾種：①對PPT的運用比較熟練;②不知道有哪些動態幾何軟件;③對軟件的功能和作用不了解。

（3）“非常愿意”和“想要嘗試”運用動態幾何軟件來輔助教學的教師總和占了總數的91.18%。

綜上所述，數學教師因對 “動態幾何”認知度不高，缺乏對動態幾何軟件的了解和運用，動態幾何的教學理念在數學課堂中并未得到廣泛的運用，但絕大部分教師對這一理念有興趣，想要在自己的課堂中進行嘗試。本文基于這一現象，結合具體實例，對“動態幾何”在培養學生空間觀念的方法與價值方面進行闡述。

二、思考：“動態幾何”的內涵特質

動態幾何是在近現代數學思想的基礎上發展起來的一種幾何思想，它起源于20世紀80年代，最初的目的是利用相應的計算機軟件代替圓規和直尺畫直線、圓及其交點等幾何圖形。

著名數學家A.H.柯爾莫戈洛夫指出：“只要有可能，數學家總是盡力把他們正在研究的問題從幾何上視覺化。”以信息技術為依托，動態幾何為這種“幾何可視化”增加了動態的元素。在眾多的動態幾何軟件中，“幾何畫板”的作用不容小覷。點、線、圓是其基本元素，一方面幾何畫板可以進行平行線、垂線等的構造，能度量圖形的周長、面積，同時它還具有多種圖形變換功能，包括平移、旋轉等;另一方面，畫板中的某些對象可以用鼠標拖動或用參數的變化來直接驅動，而其他沒有被拖動或直接驅動的對象會自動調整其位置，以保持圖形原來設定的幾何性質。它比PPT更能輕松解決“圖形運動和變化”的問題，它打破了Flash動畫只能按照設定的橋段走的局限性。它讓圖形與幾何的學習變得直觀、生動、豐富，對發展學生的空間觀念、培養創新精神和實踐能力有著十分重要的價值。本文著重描述“幾何畫板”在發展學生空間能力方面的實踐。

三、追尋：“動態幾何”的實踐策略

動態幾何貫穿于“圖形與幾何”的四大領域（圖形的認識、測量、運動與位置）學習的全過程。通過觀察、想象、比較、綜合、抽象分析的過程，發展學生的空間觀念。

（一）變“靜”為“動”，發展空間知覺

數學知識是豐富多彩的，但呈現在教材中的知識是靜態的、抽象的，如何把內隱的、壓縮的過程直觀化、外顯化，動態幾何的“動態演示”功能恰好能做到這一點。

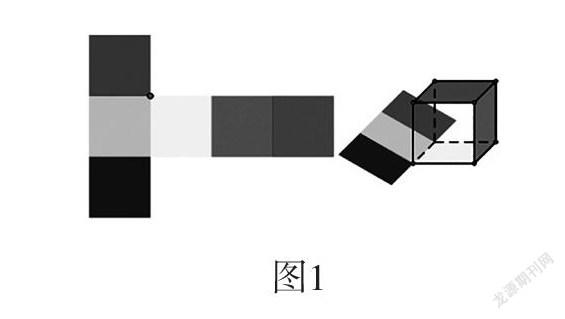
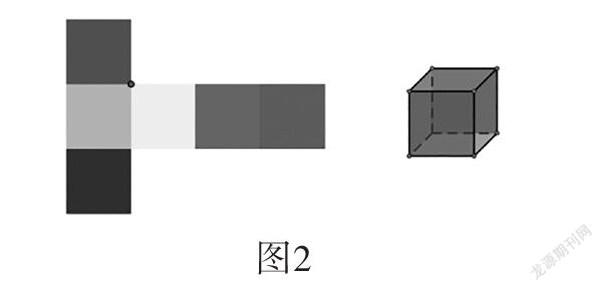
以“正方體展開圖”為例。這是蘇教版數學六年級上冊的內容，是學生在認識正方體后的一節課程。教材編排這節課的目的是通過教學正方體的展開圖來培養學生的空間觀念。在平時的教學中，教師往往直接告知學生展開圖的類型分別有“1-4-1”“2-3-1”“3-3”這三種模型，并將其對應的展開圖以圖片形式呈現。這樣的教學過程，學生的空間思維并沒有得到發展，更多的只是死記硬背。而動態幾何就能很好地把這一過程清晰地演繹出來（如圖1、圖2）。

如圖1，左側是平面展開圖，右側是立體圖，通過拖拽可以將正方體按照左側展開圖的形式一步一步展開;如圖2，也可以將展開圖還原成正方體。通過演示，讓學生經歷“立體—平面—立體”的思維過程，將靜態的、抽象的知識動態化、外顯化，學生的空間思維在一開一合之間得到了最大的發展。

認識圓柱的時候，也可以引入動態幾何。教師用幾何畫板，將一個點沿著直線運動，另一個點隨意運動，在移動的過程中利用“追蹤點”功能留下點的軌跡，學生發現點的運動軌跡可以是直線，也可以是曲線。接下來教師提問：想一想，線段的運動會形成怎樣的圖形呢？學生思考后繼續觀察幾何畫板中線段通過平移或旋轉可以得到平面圖形。此時，學生能聯想到通過面的運動就可以得到立體圖形。學生這樣的猜想是否正確，教師可以讓學生利用手中的長方形或圓形紙片自主操作，并討論交流。最后，教師通過幾何畫板來驗證：將長方形繞著線段OD旋轉，保留長方形旋轉一周的軌跡，形成圓柱（如圖3）;或將圓O沿直線方向向下拉動，留下的軌跡也是圓柱（如圖4）。

這一教學過程，由觀察靜態圖片變為問題引領下的動態動畫呈現，動態幾何豐富了幾何圖形教學的方式，化抽象為直觀，化單一表征為多元表征。通過教師的引導，學生在已有知識的基礎上進行建構，空間知覺以“零維—一維—二維—三維”的方式得到發展，教師潛移默化地滲透了平面圖形與立體圖形間的聯系，達到了知識間的內部遷移，深化了學生對“點動成線”“線動成面”“面動成體”的感知和理解。學生有了這樣的表象依托后，教師可以進一步讓學生對比不同素材旋轉后所得到的圓柱的特點，從而深刻理解圓柱的粗細、高矮與什么有關，為接下來圓柱的表面積和體積的學習打下堅實的基礎。

（二）變“散”為“連”，豐富空間表象

理論和實踐告訴我們，小學生形成、發展空間觀念主要依靠“視覺”和“觸覺”，而實踐操作是個體化的、散點狀的，引進動態幾何，在變與不變比較中，可以溝通圖形之間的聯系。

幾何畫板中的動畫功能是最基本的一項功能，在制訂路徑（線段、直線、圓等）上構造一個點，這個點就可以在既定的軌跡上往正反兩個方向運動。運動的方式可以用鼠標按住點來運動，也可以設置動畫按鈕來控制運動。下面就以兩個具體實例來闡述：

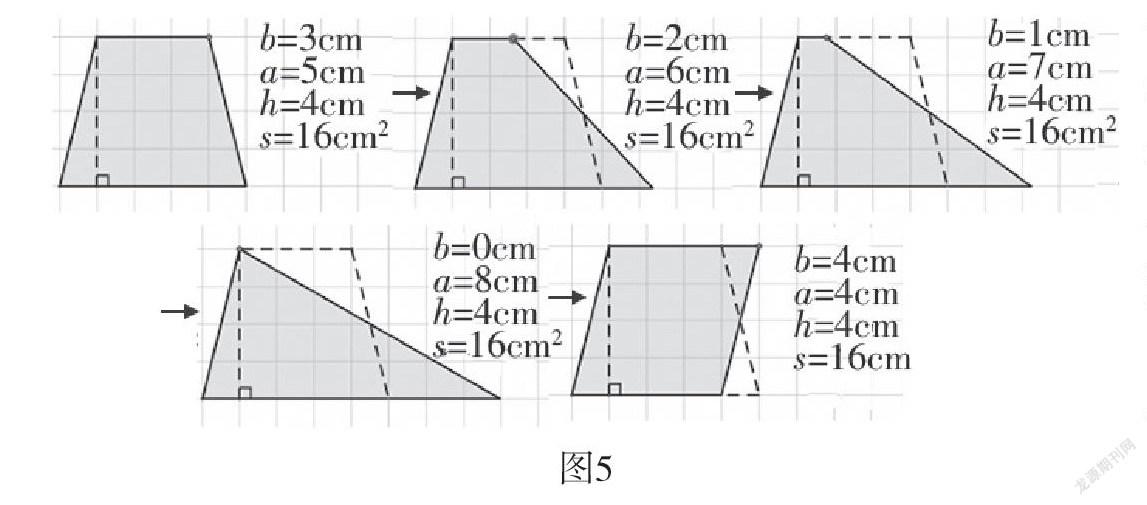
“多邊形面積的整理與復習”一課中，要求學生“在方格圖上畫一個與梯形的高和面積都相等的圖形”。教師在講解過程中，可以利用幾何畫板點的動畫功能，讓梯形右上方的一點，沿著上底所在的直線這條軌跡運動，從而制作出動畫（如圖5）：

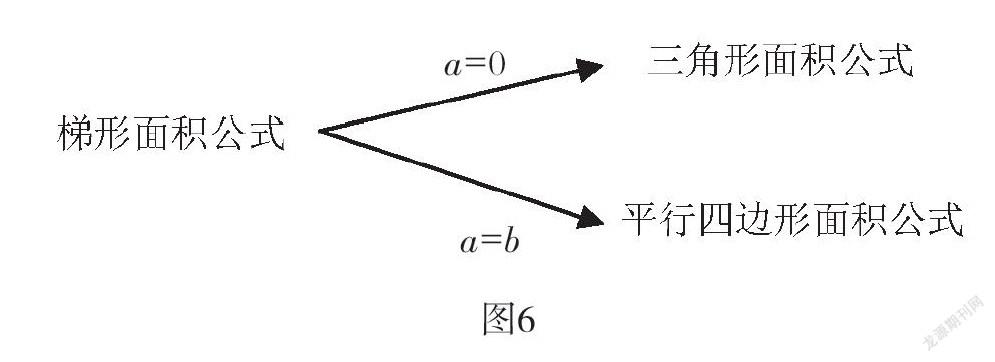
在這一開放性問題的引領下，學生自主探究，個性化表達，而在分享交流中，通過幾何圖形的動態演示，為學生直觀感知圖形間相互轉化的運動過程創造可能，盡管圖形的形狀在變，但圖形的面積沒有發生改變，本質在于平行線之間的距離處處相等。正是基于這一前提，學生在這節課中，感受到了數學的統一之美：當梯形上底縮小為0時就成了三角形，當梯形上、下底相等時就成了平行四邊形（如圖6）。

（三）變“虛”為“實”，發展空間觀念

抽象是數學的主要特征之一。基于小學生的認知特點，借助動態幾何軟件，可以給抽象的知識以直觀的支撐，讓空間觀念真實可及。在探索“三角形三邊關系”時，學生的操作體驗是這節課中必不可少的環節。但上過這節課的教師都知道，三角形的三條邊是線段，但教師準備的材料（塑料吸管、吸鐵磁條等）在圍成三角形時都會存在誤差。在教學過程中，如何合理解釋“兩邊之和等于第三邊”這種不能構成三角形的情況，是在上這節課時的一個隱藏的卻避無可避的“雷”。

利用幾何畫板就能把這個不易操作的實驗過程以動態直觀的形式真實呈現。

值得一提的是，幾何畫板中的動畫功能和Flash是有區別的：Flash中的動畫是既定的，教師一般根據教學設計提前制作，沒有實時演示功能;而幾何畫板中的動畫功能，教師可以通過右側的控制按鈕實現實時演示功能。這樣做的好處是讓課堂更具交互性，且通過兩條邊的頂點逐漸靠近，讓學生感受到兩邊之和與第三條邊相等是沒有辦法圍成三角形的，也讓學生感受到數學作為一門科學的嚴謹性。

數學結論的得出，經歷的過程一般都是“分析—假設—實驗—驗證”這四個步驟，教師在教學過程中為了讓學生感受數學這門學科的嚴謹性，都會告訴學生要進行多次實驗，才能得出正確的結論。但這個“多次實驗”往往既費時又費力。以“圓的面積”這節課為例，在推導圓面積公式的時候，教師通過將圓等分拼成類似長方形，從而推導得到圓面積的計算公式。

單純地用剪拼的操作來推導顯然太麻煩，而且效果也不理想，如果是一般的課件其預設又太單一（圓等分的份數只能事先預設，不能根據課堂生成隨機改變）， “圓等分的份數越多，拼成的圖形越像長方形”。對于這一點教師往往只能讓學生發揮想象，而對空間觀念比較薄弱的學生來說，這一過程并未在其大腦中建立表象，利用幾何畫板，就可以根據學生的回答將圓等分，把思維的過程可視化，真正做到了以“一圖應萬變”。

總之，動態幾何是為了解決傳統數學教學中難以解決的問題，是為了從根本上改變數學學習方式，有利于學生更好地理解與思考。教學中，一方面要堅持學生本位，要考慮學生的認知特點;另一方面要堅持學科本質，要考慮教學目標，讓信息技術與小學數學相輔相成，在發展空間能力的同時，實現學生數學素養的提升。

【參考文獻】

[1]毛雪琴，何姝珊.動態幾何在中學數學教學中的應用及其價值[J].高等函授學報（自然科學版），2008（3）.

[2]張文梅.幾何畫板對初中學生幾何動態問題解決的有效性探索[D].上海：華東師范大學，2010.

[3]莊振林.幾何畫板在高中解析幾何教學中的應用研究[D].呼和浩特：內蒙古師范大學，2013.

[4]李春娟.淺談小學生空間觀念的培養[J].小學教學參考，2014（23）.

[5]包靜娟.用本原性問題驅動數學理解[J].教育研究與評論（小學教育教學），2018（10）.