在高中幾何教學(xué)中發(fā)展學(xué)生核心素養(yǎng)的實(shí)踐
【摘要】本文以高中數(shù)學(xué)習(xí)題課“立體幾何中的體積問(wèn)題”為例,論述在幾何教學(xué)中培養(yǎng)學(xué)生學(xué)科核心素養(yǎng)的途徑:引導(dǎo)學(xué)生運(yùn)用“轉(zhuǎn)面”和“轉(zhuǎn)點(diǎn)”兩種技巧,將復(fù)雜的問(wèn)題簡(jiǎn)單化,將抽象的圖形直觀化,在探究中找到通法,在變式中感悟問(wèn)題的本質(zhì),發(fā)展數(shù)學(xué)抽象、直觀想象、數(shù)學(xué)運(yùn)算等數(shù)學(xué)學(xué)科核心素養(yǎng)。
【關(guān)鍵詞】高中數(shù)學(xué) 體積問(wèn)題 解題研究
變式教學(xué) 核心素養(yǎng) 立體幾何教學(xué)
【中圖分類號(hào)】G63 【文獻(xiàn)標(biāo)識(shí)碼】A
【文章編號(hào)】0450-9889(2023)29-0068-04
自2018年教育部提出學(xué)科核心素養(yǎng)以來(lái),一線教學(xué)中如何有效發(fā)展學(xué)生的核心素養(yǎng)成了各學(xué)校、教研組和一線教師思考的問(wèn)題。全國(guó)各地的數(shù)學(xué)教研員和數(shù)學(xué)教師通過(guò)開展視導(dǎo)課、研討課、優(yōu)質(zhì)課賽課等形式多樣的教研活動(dòng)研究課堂教學(xué)和解讀數(shù)學(xué)學(xué)科核心素養(yǎng)。運(yùn)用等體積法求解體積問(wèn)題是高中數(shù)學(xué)教學(xué)的重點(diǎn)和難點(diǎn)內(nèi)容,此內(nèi)容與空間中點(diǎn)、線、面的位置,以及公理定理等知識(shí)關(guān)聯(lián)緊密,對(duì)發(fā)展學(xué)生的空間想象能力,提升學(xué)生的核心素養(yǎng)具有促進(jìn)作用。本文分享筆者參加“深耕課堂、品質(zhì)教研”核心素養(yǎng)下青年教師大賽,榮獲南寧市開發(fā)區(qū)一等獎(jiǎng)的研討課教學(xué)設(shè)計(jì)——“立體幾何中的體積問(wèn)題”。該課例引導(dǎo)學(xué)生通過(guò)求解三棱錐的體積以及其他一般幾何體的體積,體會(huì)其中重要的數(shù)學(xué)思想——轉(zhuǎn)化思想,發(fā)展數(shù)學(xué)抽象、直觀想象、數(shù)學(xué)運(yùn)算等數(shù)學(xué)學(xué)科核心素養(yǎng)。
一、教學(xué)設(shè)計(jì)依據(jù)
(一)基于對(duì)課程標(biāo)準(zhǔn)的研讀
《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版2020年修訂)》(以下簡(jiǎn)稱《課程標(biāo)準(zhǔn)》)指出,數(shù)學(xué)學(xué)科核心素養(yǎng)包括數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運(yùn)算和數(shù)據(jù)分析。“立體幾何中的體積問(wèn)題”一課,主要聚焦數(shù)學(xué)抽象和直觀想象等數(shù)學(xué)學(xué)科核心素養(yǎng)的發(fā)展。
數(shù)學(xué)抽象是指通過(guò)對(duì)抽象數(shù)量關(guān)系與空間形式,得到數(shù)學(xué)研究對(duì)象的素養(yǎng)。從圖形與圖形關(guān)系中抽象出數(shù)學(xué)概念及概念之間的聯(lián)系,從事物的具體背景中抽象出一般規(guī)律和結(jié)構(gòu)。因此本課擬呈現(xiàn)第一題組,重點(diǎn)闡述“轉(zhuǎn)面”的方法。“轉(zhuǎn)面”指的是找到有線面垂直關(guān)系的面作為幾何體底面。在本教學(xué)環(huán)節(jié),教師首先呈現(xiàn)高考真題,再改編條件引導(dǎo)學(xué)生思考,通過(guò)解答題組與歸納,總結(jié)出能夠作為“垂面”的幾何面的一般特征,增強(qiáng)學(xué)生對(duì)“轉(zhuǎn)面”結(jié)構(gòu)的認(rèn)識(shí)。
直觀想象是指借助幾何直觀和空間想象感知事物的形態(tài)和變化,利用空間形式,特別是圖形,理解和解決數(shù)學(xué)問(wèn)題的素養(yǎng)。借助空間形式認(rèn)識(shí)事物的位置關(guān)系、形態(tài)變化和運(yùn)動(dòng)規(guī)律;利用圖形描述、分析數(shù)學(xué)問(wèn)題;建立形與數(shù)的聯(lián)系,構(gòu)建數(shù)學(xué)問(wèn)題的直觀模型,探討解決問(wèn)題的思路。因此,本課擬呈現(xiàn)第二題組,重點(diǎn)闡述“轉(zhuǎn)點(diǎn)”的方法。“轉(zhuǎn)點(diǎn)”指的是通過(guò)平行關(guān)系等距轉(zhuǎn)換頂點(diǎn),或通過(guò)相似,利用相似比轉(zhuǎn)換頂點(diǎn)。立體幾何涉及三大距離:點(diǎn)面距離、線面距離以及面面距離,通過(guò)設(shè)置動(dòng)點(diǎn)問(wèn)題,引導(dǎo)學(xué)生思考,在學(xué)習(xí)面面距離時(shí)設(shè)計(jì)動(dòng)畫讓學(xué)生能夠直觀觀察,總結(jié)出“平行轉(zhuǎn)化”和“比例轉(zhuǎn)化”兩種解決具體問(wèn)題的基本模型,將未知問(wèn)題轉(zhuǎn)化為已知問(wèn)題,進(jìn)而解決。
(二)基于引導(dǎo)學(xué)生思維自然發(fā)展的思考
數(shù)學(xué)教學(xué)中蘊(yùn)含著思維的體操、知識(shí)的傳導(dǎo)、方法的掌握和思想的領(lǐng)悟等,這些都有助于學(xué)生思維的發(fā)展。筆者一直秉持以生為本的理念,致力于站在學(xué)生的角度設(shè)計(jì)符合學(xué)生思維發(fā)展的教學(xué)流程,自然而有層次地促進(jìn)學(xué)生數(shù)學(xué)思維的發(fā)展。
筆者在《數(shù)列課堂教學(xué)中教師思維引導(dǎo)的理論與實(shí)踐研究》一文中曾嘗試根據(jù)教師在課堂教學(xué)引導(dǎo)學(xué)生思維發(fā)展的情況,結(jié)合《課程標(biāo)準(zhǔn)》中目標(biāo)動(dòng)詞層次劃分,進(jìn)一步對(duì)“自然度”進(jìn)行以下六個(gè)層次的描述。
自然度0:學(xué)生不知道基本的知識(shí),如概念、原理等,無(wú)法參與教學(xué)活動(dòng),不能理解教師所講解的知識(shí)及過(guò)程、結(jié)論。
自然度1:學(xué)生能了解教師的教學(xué)過(guò)程,通過(guò)模仿經(jīng)歷教學(xué)過(guò)程,對(duì)教師的觀點(diǎn)和教學(xué)過(guò)程持認(rèn)同的態(tài)度。
自然度2:學(xué)生理解教師所教知識(shí)內(nèi)容,并嘗試獨(dú)立完成,能在教師的指導(dǎo)下領(lǐng)悟教學(xué)內(nèi)容。
自然度3:學(xué)生能解釋知識(shí)內(nèi)容,能對(duì)內(nèi)容進(jìn)行整理,形成自己的認(rèn)知形式。
自然度4:學(xué)生能提取出其中的核心知識(shí),對(duì)教學(xué)過(guò)程進(jìn)行清晰的分析,并能樹立正確的價(jià)值觀。
自然度5:學(xué)生可以用聯(lián)系的方法來(lái)理解所學(xué)內(nèi)容,并能遷移運(yùn)用,能對(duì)教學(xué)過(guò)程做出正確的評(píng)價(jià),發(fā)展對(duì)數(shù)學(xué)的認(rèn)識(shí)。
因此,本節(jié)課擬從復(fù)習(xí)基礎(chǔ)知識(shí)入手,做好教學(xué)活動(dòng)鋪墊,在變式教學(xué)中搭建合適的教學(xué)階梯——等體積轉(zhuǎn)換求同一三棱錐體積,為使教學(xué)由自然度0不斷提升至自然度5鋪墊。第一題組為直接求體積、“轉(zhuǎn)面”,在此基礎(chǔ)上設(shè)計(jì)“比例轉(zhuǎn)換”,將所求圖形的高轉(zhuǎn)換為已知高,促使學(xué)生在解決問(wèn)題時(shí)更易突破難點(diǎn)。第二題組無(wú)法直接“轉(zhuǎn)點(diǎn)”,教師需提出問(wèn)題并搭建教學(xué)支架:線面平行則直線上任意一點(diǎn)到平面的距離相等,從而實(shí)現(xiàn)“轉(zhuǎn)點(diǎn)”,接著再“轉(zhuǎn)面”,最后將問(wèn)題從三棱錐這一特殊空間幾何體遷移至四棱錐等更一般的幾何體中,促使學(xué)生對(duì)體積問(wèn)題有更深層次的認(rèn)識(shí)。在整個(gè)教學(xué)過(guò)程中,注重變式和問(wèn)題串的設(shè)計(jì),在問(wèn)題解決的過(guò)程中,使學(xué)生的思維得到有效發(fā)展,讓學(xué)生有機(jī)會(huì)質(zhì)疑、思考,發(fā)展創(chuàng)造性思維,有機(jī)會(huì)思考和提出自己的見(jiàn)解。在最佳時(shí)機(jī),教師提供恰當(dāng)?shù)乃季S引導(dǎo),如強(qiáng)化運(yùn)算、模仿等,促進(jìn)學(xué)生深入地思考問(wèn)題內(nèi)在的邏輯。在思維引導(dǎo)過(guò)程中,教師要遵循思維循序漸進(jìn)發(fā)展的規(guī)律,讓學(xué)生體會(huì)到某個(gè)階段自然地想到解決問(wèn)題的方法,使學(xué)生的思維自然地獲得發(fā)展。
在此教學(xué)設(shè)計(jì)中,筆者主要以一道高考真題為原型進(jìn)行改編,讓學(xué)生在變式中體會(huì)“轉(zhuǎn)面”“轉(zhuǎn)點(diǎn)”的依據(jù)和原理,找出其中的一般規(guī)律,提高學(xué)生提出問(wèn)題、分析問(wèn)題和解決問(wèn)題的能力。
二、教學(xué)設(shè)計(jì)要點(diǎn)
(一)教材分析及學(xué)情分析
本節(jié)課內(nèi)容為高中數(shù)學(xué)的高頻考點(diǎn)。解答體積問(wèn)題對(duì)學(xué)生空間立體感要求較高,要求學(xué)生能夠理解并靈活運(yùn)用公理和定理。學(xué)生在本節(jié)課之前已經(jīng)復(fù)習(xí)了通過(guò)直接法求幾何體體積,本節(jié)課著重分析從“轉(zhuǎn)面”和“轉(zhuǎn)點(diǎn)”兩個(gè)角度求錐體體積的“等體積法”。
(二)教學(xué)目標(biāo)與教學(xué)重難點(diǎn)
本節(jié)課設(shè)計(jì)了三個(gè)教學(xué)目標(biāo):一是掌握運(yùn)用等體積法中“轉(zhuǎn)面”的方法求三棱錐體積;二是掌握運(yùn)用“轉(zhuǎn)點(diǎn)”中的平行轉(zhuǎn)移和比例轉(zhuǎn)換求幾何體體積;三是體會(huì)在求解體積過(guò)程中的轉(zhuǎn)化思想。
本課重點(diǎn)共兩個(gè):一是掌握利用“轉(zhuǎn)面”“轉(zhuǎn)點(diǎn)”的方法求幾何體體積;二是體會(huì)求解過(guò)程中的轉(zhuǎn)化思想。本課難點(diǎn)也是兩個(gè):一是利用等體積法求幾何體體積時(shí)如何“轉(zhuǎn)面”;二是“轉(zhuǎn)點(diǎn)”過(guò)程中,理解平行轉(zhuǎn)換中的高的不變性、比例轉(zhuǎn)換中高成相似比。
(三)設(shè)計(jì)思路
在教學(xué)設(shè)計(jì)中,將高考真題改編為例1,隨后變式為例2。例1介紹通過(guò)“轉(zhuǎn)面”實(shí)現(xiàn)等積轉(zhuǎn)換,例2主要通過(guò)“轉(zhuǎn)點(diǎn)”實(shí)現(xiàn)等積轉(zhuǎn)換或者體積比例轉(zhuǎn)換。
三、教學(xué)過(guò)程
(一)“轉(zhuǎn)面”
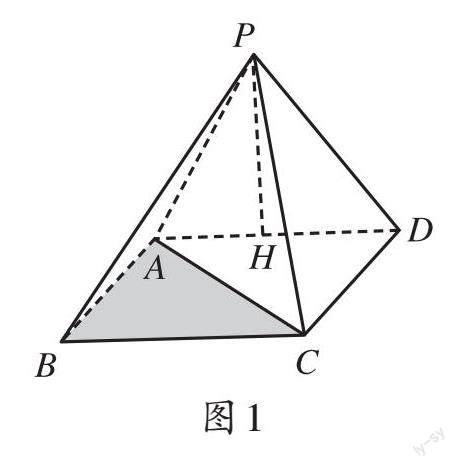
例1:如圖1,在四棱錐中,底面ABCD為矩形,△PAD為邊長(zhǎng)為2的正三角形,AB=[3],且平面PAD⊥平面ABCD,求三棱錐A-PBC的體積。
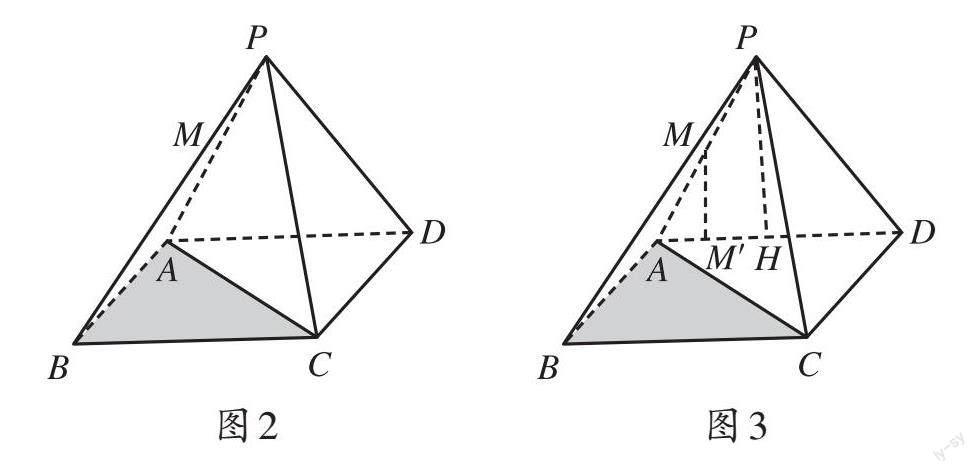
變式:如圖2,在四棱錐中,底面ABCD為矩形,△PAD為邊長(zhǎng)為2的正三角形,AB=[3],且平面PAD⊥平面ABCD,M為AP中點(diǎn),求三棱錐A-MBC的體積。
【設(shè)計(jì)意圖】當(dāng)幾何體所給面上找不到高或者不好求高時(shí),分析題目條件,可以將有線面垂直關(guān)系的面作為底面。本題組重點(diǎn)介紹等體積法中利用“轉(zhuǎn)面”求幾何體體積的方法,在變式中用中點(diǎn)引出比例轉(zhuǎn)換(如上頁(yè)圖3所示),為后面比例轉(zhuǎn)換做鋪墊。
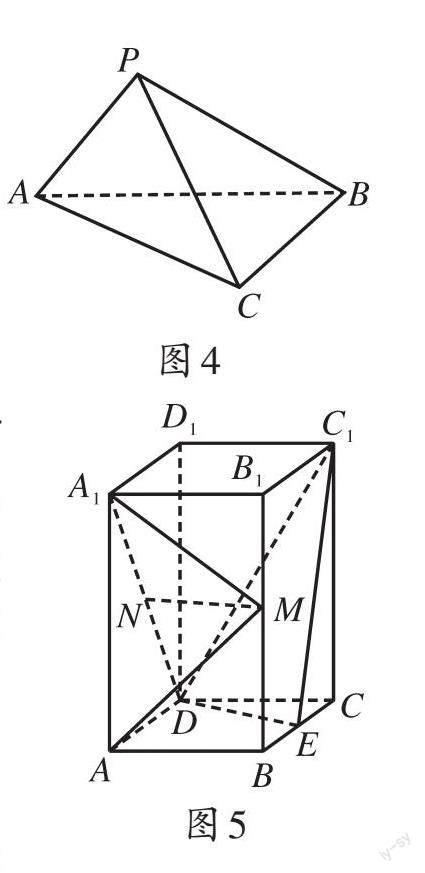
鞏固練習(xí):1.如圖4,在三棱錐中,△ABC為等邊三角形,AB=2,PA=1,∠PAC=∠PAB=60°,求三棱錐P-ABC的體積。
2.(2019年全國(guó)I卷,理科,第18題)如圖5,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E、M、N分別是BC、BB1、A1D的中點(diǎn)。(1)證明MN∥平面C1DE。(2)求二面角A-MA1-N的正弦值。
【設(shè)計(jì)意圖】給出兩個(gè)不同類型的幾何體,師生合作分析如何“轉(zhuǎn)面”,找出有垂線的面,突破第一個(gè)難點(diǎn)。在“轉(zhuǎn)面”的過(guò)程中總結(jié)得出:將幾何體中的懸空面轉(zhuǎn)換到原幾何體的表面,則可以運(yùn)用原直棱柱線面垂直的條件求解,這是“轉(zhuǎn)面”常用的方法,同時(shí)為第二題組中先“轉(zhuǎn)面”,進(jìn)而再“轉(zhuǎn)點(diǎn)”的綜合應(yīng)用做鋪墊。
(二)“轉(zhuǎn)點(diǎn)”
例2:如圖6,在四棱錐中,底面ABCD為矩形,PA⊥平面ABCD,且AP=1,AB=2,AD=[3],M、N分別為PD、PB的中點(diǎn)。(1)證明PB//平面AMC;(2)求四面體AMNC的體積。
分析1:四面體的四個(gè)面為懸空面,找垂面為第一個(gè)難點(diǎn)。
分析2:解答第一問(wèn)時(shí),連接BD與AC交于點(diǎn)Q,易證PB//MQ,于是PB//平面AMC,因此PB上的點(diǎn)到平面AMC的距離相等,從而可以將N點(diǎn)轉(zhuǎn)為B點(diǎn)或P點(diǎn),實(shí)現(xiàn)將懸空面轉(zhuǎn)換為幾何體表面。這里運(yùn)用了平行等距轉(zhuǎn)換。
【設(shè)計(jì)意圖】在例1的基礎(chǔ)上變式,幾何體中每個(gè)面都沒(méi)有垂直關(guān)系,介紹通過(guò)平行轉(zhuǎn)移的方法“轉(zhuǎn)點(diǎn)”,實(shí)現(xiàn)轉(zhuǎn)換。在此過(guò)程中也介紹“轉(zhuǎn)點(diǎn)”過(guò)程中常用的第二種方法——比例轉(zhuǎn)換求體積。
鞏固練習(xí):1.如圖7,在棱長(zhǎng)為2的正方體ABCD-A1B1C1D1中,點(diǎn)P在線段AD1上運(yùn)動(dòng),求四面體BDPC1的體積。
2.如圖8,在三棱柱ABC-A′B′C′中,點(diǎn)D是AC′的中點(diǎn),點(diǎn)E是B′C′的中點(diǎn)。(1)求證:DE∥平面ABB′A′;(2)若△ABC的面積為[3],三棱柱ABC-A′B′C的高為3,求三棱錐D-BCE的體積。
【設(shè)計(jì)意圖】鞏固練習(xí)1考查平行轉(zhuǎn)換“轉(zhuǎn)點(diǎn)”,鞏固練習(xí)2考查比例轉(zhuǎn)換“轉(zhuǎn)點(diǎn)”。師生合作分析如何“轉(zhuǎn)點(diǎn)”,突破第二個(gè)難點(diǎn)。還可以運(yùn)用割補(bǔ)法作差求解鞏固練習(xí)2,幫助學(xué)生完善解答幾何體體積的知識(shí)網(wǎng)絡(luò)。
(三)布置課后作業(yè),拓展提升
1.如圖9,正方體ABCD-A1B1C1D1中,點(diǎn)P在線段B1C上運(yùn)動(dòng),則下列命題中正確的是(? )。
①直線AP//平面A1C1D;②三棱錐P-A1C1D的體積為定值;③若M為AP上的動(dòng)點(diǎn),則三棱錐M-A1C1D不是定值。
2.如圖10,四邊形ABCD中,AB//CD,BC=CD=DA=[12],AB=2,E為AB的中點(diǎn),以DE為折痕將△ADE折起,使點(diǎn)A到達(dá)點(diǎn)P的位置,且平面PDE⊥平面BCDE,F(xiàn)為PB的中點(diǎn)。(1)求證:PD//平面CEF;(2)求三棱錐P-DEF的體積。
【設(shè)計(jì)意圖】課后作業(yè)共兩道題,學(xué)生需綜合運(yùn)用“轉(zhuǎn)面”“轉(zhuǎn)點(diǎn)”的方法求體積,考查學(xué)生對(duì)本節(jié)課重難點(diǎn)的掌握程度,同時(shí)讓學(xué)生接觸高考題型中的不定項(xiàng)選擇題。
(四)課堂小結(jié)
教師運(yùn)用思維導(dǎo)圖,帶領(lǐng)學(xué)生梳理、總結(jié)與立體幾何中的體積問(wèn)題有關(guān)的基礎(chǔ)知識(shí)、基本題型和基本數(shù)學(xué)思想方法(如下頁(yè)圖11所示)。
四、教學(xué)反思
本節(jié)課主要呈現(xiàn)兩個(gè)題組:題組一考查“轉(zhuǎn)面”等體積轉(zhuǎn)換,主要為在幾何體所給底面找不到高或高不好求的情況下,將有線面垂直關(guān)系的面轉(zhuǎn)化為底面,求出高,進(jìn)而等積求解;題組二考查“轉(zhuǎn)點(diǎn)”,主要分析當(dāng)幾何體中沒(méi)有直接可以找到高的面時(shí),引導(dǎo)學(xué)生通過(guò)“轉(zhuǎn)點(diǎn)”,進(jìn)而實(shí)現(xiàn)“轉(zhuǎn)面”、求體積,主要介紹常用的平行轉(zhuǎn)換和比例轉(zhuǎn)換。
鞏固練習(xí)題組注重難度遞進(jìn),選題注重幾何體的多樣性,符合《課程標(biāo)準(zhǔn)》提出的發(fā)展學(xué)生基本素養(yǎng)、發(fā)展學(xué)生空間想象能力的要求。題目涉及解三角形,這是求高、求面積的常用方法。采用這種方法既可以引導(dǎo)學(xué)生關(guān)聯(lián)函數(shù)知識(shí),又可以強(qiáng)化學(xué)生解答立體幾何問(wèn)題的能力。
課后作業(yè)中的兩道拓展練習(xí)題,給學(xué)生課后思考指明方向,學(xué)生可以綜合運(yùn)用本節(jié)課所學(xué)的多種方法進(jìn)行解答。這些方法可以提升學(xué)生分析圖形和數(shù)學(xué)計(jì)算的能力,使其領(lǐng)會(huì)轉(zhuǎn)化思想。
作者簡(jiǎn)介:李婷(1989— ),湖南長(zhǎng)沙人,碩士,一級(jí)教師,主要研究方向?yàn)榛A(chǔ)數(shù)學(xué)研究和德育研究。
(責(zé)編 劉小瑗)

