基于具身認知理論的高中數學生本課堂*

【摘 要】圓錐曲線與方程是高中數學的重要內容之一。研究圓錐曲線有兩個重要任務：一是研究它的概念及其標準方程，二是研究其性質。在研究的過程中，教師可以基于具身認知理念，引導學生通過體悟、探索、實驗以及遷移，實現自主探究學習、深度學習，從而落實數學核心素養的培養，打造生本課堂。

【關鍵詞】高中數學；概念數學；橢圓；具身認知；核心素養

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2024）15-0041-04

【作者簡介】崔緒春，江蘇省清江中學（江蘇淮安，223001）教師，正高級教師。

“具身認知”（Embodied Cognition）指人類思維和感知過程不僅來自于大腦神經系統，還與身體的運動、肌肉和感知器官的活動密切相關。具身認知理論啟示教師要不斷創造條件，鼓勵學生通過多種感官訓練手段去體悟、探索、實踐，從而促成探究學習、深度學習。［1］下面筆者以蘇教版高中數學選擇性必修一“橢圓概念”教學為例，闡述“具身認知”理論下的高中數學生本課堂的實踐探索。

一、教學分析

（一）教學內容分析

圓錐曲線是高中數學的重要內容之一，研究圓錐曲線不是用規律推理形式，而是運用代數方法解決幾何問題，即用方程的解來表征幾何結論，這是“數形結合”思想的重要體現。“橢圓概念”是圓錐曲線章節起始課，由于橢圓與雙曲線、拋物線是同構的，研究好橢圓的概念及其標準方程，對本章后續知識的學習具有基礎性與示范性作用。教材中直接給出橢圓定義，學生容易“知其然”但“不知其所以然”，對橢圓幾何屬性的認知不夠透徹。因此，教學中筆者參考教材的章節導入內容，嘗試依據歷史上數學家對于橢圓幾何性質的探究，帶領學生從具體情境中抽象出橢圓的幾何本質，經歷完整的橢圓概念生成過程。

（二）教學目標

1.初步了解橢圓等圓錐曲線的現實背景，感知橢圓等圓錐曲線在解決具體問題和表述現實世界方面的作用；

2.以具身認知理論為指導，通過“旦德林雙球”實驗，引導學生抽象、歸納出橢圓的定義，并能夠用恰當的自然語言、符號語言進行表征。

二、教學流程

（一）課堂引入：看一看

播放視頻：“天問一號”成功進入預定軌道。

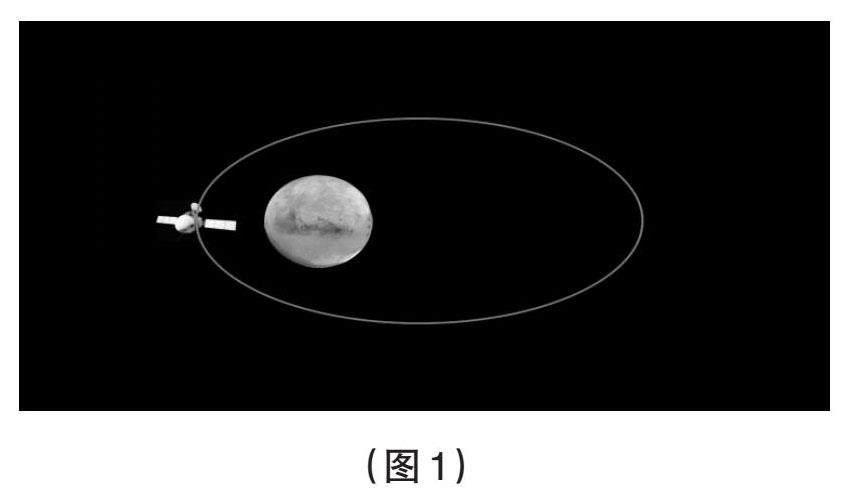
師：“天問一號”在蒼穹中劃過了一道優美的曲線（如圖1），這條軌道曲線叫什么名字？

【設計意圖】通過觀看視頻，學生了解了我國的火星探測工程，了解了圓錐曲線的航天應用，在引入新課的同時，激發了學生的愛國情懷和民族自豪感。

（二）問題提出：說一說

師：衛星運行的軌跡是橢圓。生活中還有哪些橢圓？請舉例說明。

生：油罐車橫截面，陽光斜照下籃球的影子，斜削火腿腸截面，雞蛋的縱截面……

師：同學們善于用數學眼光觀察世界，舉的例子都很好！但是你能確定這些例子都是橢圓嗎？是不是只要把圓壓扁一點就是橢圓呢？究竟什么樣的圖形才是橢圓？讓我們帶著這些問題開始今天的學習。

【設計意圖】上述教學旨在引導學生提出問題。通過對話，引發學生的認知沖突，讓學生自然而然產生這些問題，引導他們從數量關系上定量地去思考橢圓，實現學生自主探究學習。

（三）實驗感知：想一想

師：同學們，“跟著感覺走”明顯不行，我們必須從數量關系上定量地去思考橢圓的定義。如何從數量關系上定義橢圓？橢圓有什么性質？為了解決這個問題，歷史上很多數學家深入探究，通過數量關系描述了橢圓上的點的規律。這個規律是什么呢？現在就讓我們一起沿著數學家走過的歷程，揭開它神秘的面紗。

1.知識預備

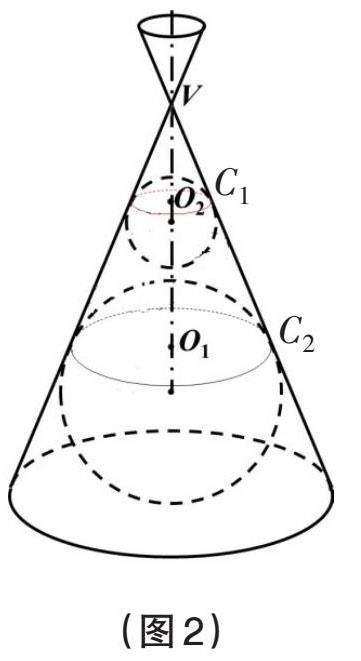
如圖2，在一個圓錐內，上下放置兩個小球，容易得到：它們與圓錐側面的公共點形成兩個圓，我們把這兩個圓記作圓C1和圓C2。［2］

學生分小組討論研究以下問題。

【問題1】圓C1與圓C2所在平面平行嗎？

【問題2】取圓C1與圓C2之間的線段PQ，讓PQ與圓錐母線平行，請問PQ與兩小球相切嗎？

【問題3】若將線段PQ保持與圓錐母線平行，繞著圓錐的側面轉動一圈，線段PQ的長度變不變？為什么？

2.橢圓幾何性質的探索

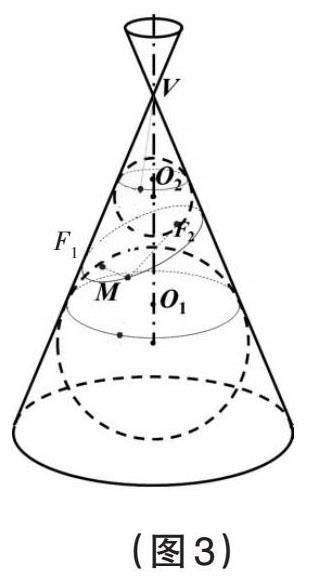
操作1：如下頁圖3，在圖2基礎上，用一個平面斜截圓錐得到橢圓形交線，并讓橢圓所在平面與兩個小球相切，記切點為F1，F2，在橢圓上任取一點M，連接MF1，MF2。

操作2：如下頁圖4，現在過點M作之前那樣的PQ，由之前得到的結論：MF1，MP都與上方小球相切，所以│MF1│=│MP│（切線長相等），同理，│MF2│=│MQ│。

師：通過觀察推理可得，當點M在橢圓上運動時，MF1，MF2分別與上下兩個小球總相切。現在，讓我們想一想剛才的問題“能否用數量關系表示橢圓上的點的運動規律？”請同學們按照小組，繼續討論以下問題。

【問題4】除了線段PQ的長度之外，在橢圓所在平面內，還有什么幾何量是不變的嗎？

【問題5】當點M在橢圓上運動時，點F1，F2的位置不發生變化。能否用語言描述一下：橢圓上的點應具有怎樣的性質呢？

學生通過對問題的自主探究和交流討論得到橢圓的性質：橢圓上的任意一點到兩個定點的距離之和為常數，其中兩個定點叫作橢圓的焦點，焦點之間的距離稱為焦距，即：│MF1│+│MF2│=│MP│+│MQ│=│PQ│= 定值。

3.了解數學史

師：同學們，這個數學實驗是19世紀比利時數學家旦德林給出的，旦德林在圓的切線與圓錐等領域研究上取得了突出成就，聞名世界的“旦德林雙球”就是用他的名字命名的，我們要學習數學家旦德林勇于探索的創新精神。正是因為通過一平面截圓錐面，可以得到橢圓、雙曲線、拋物線，所以橢圓、雙曲線、拋物線才被稱為圓錐曲線。

【設計意圖】通過圓錐背景下的“旦德林球”，探索并發現橢圓的本質特征是本節課的難點。學生了解橢圓發展史上旦德林的經典證明，體會數學家巧妙的數學方法——構造法，并進行數學文化滲透。

（四）數學建構：畫一畫

師：同學們，通過剛才的實驗，我們研究出了橢圓的幾何性質，即橢圓上的任意一點滿足到兩定點距離之和為定值的數量關系。反過來，滿足這一數量關系的點的軌跡是否是橢圓呢？下面我們來畫橢圓，看看滿足條件的點的軌跡是否為橢圓。

活動方案：（1）拿出準備好的硬紙板、圖釘、細線；（2）用圖釘固定好F1、F2，把細線兩端固定在圖釘上，用筆撐直繩子，同桌兩人共同配合，讓筆與繩之間是自由運動的，這樣轉動一周，畫出的圖形就是橢圓（如圖5）。

學生在活動探究的基礎上思考以下問題。

【問題6】畫橢圓時，PF1，PF2的距離之和為什么要大于點F1，F2之間的距離？

【問題7】為什么這樣畫出來的圖形就是橢圓？

師：平面內到兩個定點F1，F2的距離之和等于常數2a（2a大于│F1F2│）的點的軌跡叫作橢圓。兩個定點F1，F2叫作橢圓的焦點，兩個焦點間的距離叫作橢圓的焦距。當2a =│F1F2│時，軌跡為線段F1F2；當2a＜│F1F2│時，軌跡不存在。

【設計意圖】通過畫橢圓的活動，學生對橢圓的本質特征有了更深刻的認知，更直觀地體會了橢圓定義，為后續研究橢圓標準方程作鋪墊。

（五）知識應用：做一做

例1：若動點M（x，y）到定點F1（-4，0）和F2（4，0）的距離的和為10，則動點M的軌跡為（? ? ）

A.橢圓? ?B.雙曲線? ?C.線段? ?D.圓

變式1：動點M（x，y）到定點F1（-4，0）和F2（4，0）的距離的和為8，則動點M的軌跡是? ? ? 。

變式2：動點M（x，y）到定點F1（-4，0）和F2（4，0）的距離的和為6，則動點M的軌跡是? ? ? 。

變式3：方程[x2+（y+4）2]+[x2+（y-4）2]=10表示的曲線是? ? ? 。

【設計意圖】通過幾道題目，學生進一步明確橢圓的定義，在概念的辨析中增強學生對橢圓概念的理解與記憶，為后續推導橢圓的標準方程作鋪墊。

（六）反思提煉：悟一悟

（1）同學們，請回顧今天的學習內容，大家有哪些收獲？

（2）詩歌欣賞：

橢圓

偏行已是欲離轍，浩瀚星空藉此歌。

一種相思天注定，月盈之夜兩心合。

三、教學反思

（一）基于具身認知，促進學生深度學習

上述教學基于“具身認知”理論，通過橢圓性質探究、畫橢圓等數學實驗，讓學生沿著數學家的思路探究、歸納橢圓的概念。教學以展示學生的研究成果為主，教師主要引導學生在探究的過程中逐漸形成觀察發現、積極思考的習慣。這個過程既發展了學生數學概括、抽象能力和合作意識，又落實了教學核心素養培養要求。當視覺、聽覺、直覺、身體都共同作用時，學生腦中烙下了深刻的印象，這樣的教學很大程度上提高了學習的深度，讓學習活動真正發生。

（二）突出主體地位，促使學生主動發展

本節課突出學生主體，所有問題都是學生自己動手、動腦去探索和“再創造”的。在這樣的教學情境下，學生的思想是開放的、靈活的，能產生更多的“生成的東西”，能體驗到更多成功感和愉悅感。這種教學法與傳統的以教師為中心的教學相比，有以下優點：以學生為中心，有效調動了學生學習的積極性；有利于發展學生的數學思維能力；培養了學生的合作學習意識；培養了學生的主動探究意識與創新精神。［3］

（三）設計鏈式問題，促使學生思維創新

根據“學生最近發展區”理論，筆者為了讓學生理解旦德林雙球實驗，突破難點，精心設置了7個問題，形成了問題鏈，步步相連、逐步推進，這不僅有利于啟迪學生的思維，還能加深學生對橢圓本質的認識，同時通過這些問題的解決，鞏固了學生對橢圓概念的理解，有效地激發學生自己去探索、研究。筆者認為在課堂教學中，教師提出的問題，就要像一根鏈條，每個問題都是鏈條上的一環，環環相扣，步步相依，由淺入深，拾級而上，呈現梯度性。這樣能夠充分暴露學生的思維過程，拓展學生的數學思路。

【參考文獻】

［1］李昱蓉.具身學習：立足學科核心素養的學習方式［J］.當代教育科學，2017（9）：7-10.

［2］徐迪斐.“圓錐曲線”起始課教學設計［J］.中國數學教育，2015（10）：2-8.

［3］崔緒春.新課程理念下課堂上如何啟迪學生的數學思維［J］.中學數學，2014（17）：12-13.