數形結合思想在“數與形”教學中的實踐與思考
俞波
[摘 要]數學課程的設計要引發學生的數學思考,讓學生體會數學的基本思想和思維方式,能比較清楚地表達自己的思考過程與結果。”在認真分析教材的基礎上,教師要活用教材,給予學生獨立思考的機會和平臺,通過建構模型,幫助學生在“數與形”的教學中形成數學思維,對數形結合思想有深刻的認知。
[關鍵詞]數形結合;直觀;數學思維;實踐與思考
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2018)05-0038-02
【教材分析】
1.解題策略直觀,易于激發學生興趣
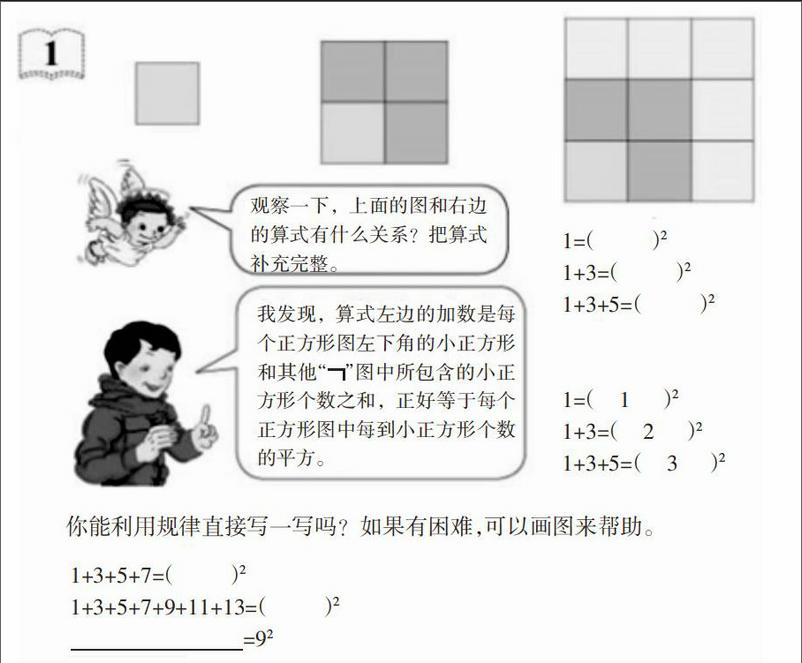
“數與形”一課最大的優點是一目了然。如例1(如下圖),圖中的算式與圖形一一對應,學生立刻就能感受到數形結合的美。在之前的教學中,數形結合思想已多有涉及,所以在六年級教學數與形的專題,其實是促進學生原有知識生長。
2.題目類型多樣,便于拓展思維寬度
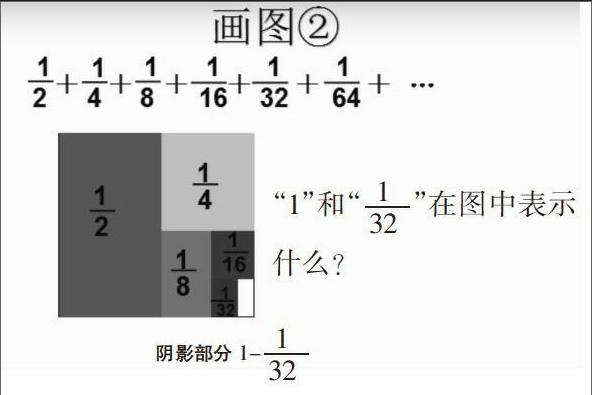
例1是利用各種不同的圖形來揭示數的規律,讓學生學會用圖形的面積、數量、邊長等不同維度的量來建立等式關系,其重點是揭示規律。而例2“計算1/2+1/4+1/8+1/16+1/32+1/64+…”屬于利用圖形來計算有規律的算式,目的是引導學生運用圖形解決計算問題。例1和例2雖然都是典型的數形結合的題目,但它們并不屬于同一個計算范疇,有利于拓展學生的思維寬度。
3.思考方法抽象,利于培養建模能力
例2展示的是用圖形表示抽象的算式,但要想到用這種方法是需要一定的數學能力的,這就給教師培養學生的建模意識創造了機會和條件。
【實踐研究】
一、活用教材,優化思考方法
1.用數學的眼光觀察圖形
教學例1時,若直接出示課本中的算式和圖形,大部分學生都不能夠將圖形與算式聯系起來,教師最終只能直白地告知他們例題的思想,數學思考的重要價值就會因此喪失。對此,筆者采用繪畫的方式引入教學內容。
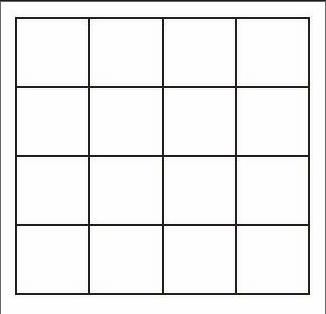
師:老師畫了一個圖,你們想看嗎?(課件出示圖形,如右圖所示)你們能否從數學的角度來找出這幅圖中蘊含的數呢?
生1:42=16。
師:逐一涂上顏色,你還能寫出一些等式來嗎?
生2:1=12,1+3=22,1+3+5=32,1+3+5+7=42。
用這樣的方式呈現例題,有利于學生深入解讀和認識圖形,更有利于后續將算式與圖形進行對比思考,真正用數的抽象揭示圖的神秘。
2.根據等式的變化尋找規律
上面這道例題的計算稍顯簡單,為此教師需要給學生制造一些思維沖突。
師:根據上面的等式和圖形,你有什么發現?
生3:1+3+5+7+9=52,1+3+5+7+9+11+13+15+17+19=102。
生4:從1開始的連續n個奇數的和等于n2。
生5:重點要注意“連續”“奇數”“從1開始”。
這種讓學生尋找算式規律的方式,使得學生能夠更快速地掌握算式的特性,也能尋找到圖形屬性與算式的聯系。
3.利用規律解決問題
師:根據例1的結論算一算。1+3+5+7+5+3+1=( ),1+3+5+7+9+11+13+11+9+7+5+3+1=( )。
讓學生利用例1的規律解決問題,使之充分體驗用數據揭示形的神秘的樂趣,很好地實現了預期的教學目標:讓學生感知數形結合的好處,知道用圖形來說明數的規律可以事半功倍。
二、創設平臺,引發解題感悟
1.給予機會獨立思考,思維有深度
教師適當放手,給予學生獨立思考的機會,是實現深度思考的重要途徑。如例2,“計算1/2+1/4+1/8+1/16+1/32+1/64+…”的教學。首先,教師請學生說一說題目的具體含義,啟發學生弄明白省略號的具體意思以及分母的變化規律;其次,教師追問:“這樣的題目你覺得該怎么解答?”學生提出的方法有通分計算、猜測規律、畫圖驗證等。這樣就很好地實現了教學目標:實踐操作,學會數形結合的具體操作方法,感知到可以用線段、正方形、圓等圖形來揭示數據的規律。
2.提供平臺深入探究,學習有寬度
進行探究實踐,是學生領悟數學思想的最佳策略。
(1)通分計算,尋找規律
師:通過計算“1/2+1/4+1/8+1/16+…=”,你發現了什么?
生6:隨著加數的增加,結果逐漸變大,越來越接近1。
師:為什么最后結果接近于1?(啟發學生發現畫圖的優越性——直觀)
(2)繪制圖形,展示過程
首先,請學生上臺講解自己畫的圖形。
其次,教師在學生展示的基礎上利用課件出示與各種圖形對應的思維過程。
揭示:陰影部分的和=1-式子中的最后一個分數。
揭示:空白不斷變小,逐漸接近0,陰影部分就不斷變大直到接近于1。
這樣的探究活動,不僅讓學生深刻地理解了數與形的內涵,更使學生突破教學重難點,有利于學生不斷拓展數學學習的寬度。
3.幫助學生形成策略,收獲有厚度
學生獨立探究后給出了各種圖形,教師將這些圖形放在一起,并提問:“通過畫圖來解決問題有什么好處?”最后,教師總結:“同樣是揭示分數的計算規律,我們可以用不同的圖形來實現,可以用線段、可以用正方形、也可以用圓,也許還有別的圖形。”這樣的回味學習將使得學生的收獲具有厚度。
三、借助模型,形成數學思維
1.數形結合突破難點——從學習的基礎出發
數學廣角的內容都比較抽象,因此,在教學過程中教師要給出一些具體、形象、直觀的圖形去幫助學生理解。endprint
師:當遇到難題或比較復雜的問題時,你會用什么辦法解決?(畫圖)為什么喜歡畫圖?
師:如果題目本身就是圖形題,怎么辦?(找出圖形中的規律)
師:像之前用圖形來解決相關問題的方法就是數形結合的方法,以前學過的內容有用到這種方法嗎?(加減法的意義、分數意義等)
師:下面的算式與圖形分別有什么樣的關系?
(a+b)c=ac+bc,(a+b)2=a2+2ab+b2
通過研究算式與圖形的對應關系,用式子描述圖形面積,用圖形面積刻畫式子,兩相對照,學生就能深刻感知數形結合的重要性。
2.圖形推算落實重點——從學習的過程出發
本課重點是讓學生經歷推理和探究圖形與算式之間關系,滲透數形結合的思想。為此,首要的是將數與形關聯在一起的本質找出來。教師可提問:“前面的例題是利用圖形的什么維度來建立關系的?”
3.抽象建模實現拓展——從學習的方法出發
本課的靈魂是抽象建模,首先要讓學生建立解決此類問題的模型;其次要讓學生形成思考和推理的意識。為此,教師可進行拓展練習,通過在練習中運用數形結合解決問題,凸顯其實用性,同時引導學生感知數形結合不單是用圖形來解決數的問題的,其實很多圖形中也蘊含著數的規律。
如用數的抽象來揭示圖形的神秘:
照這樣下去,第n個圖形有( )個紅色小正方形和( )個藍色小正方形。
這樣就能讓學生明白做這樣的題目首先要揭示圖形個數的規律,并且要用前面個數少的圖形中去揭示和發現這個規律,這是解決問題的基本技巧。
4.回顧過程完成梳理——從學習的序列出發
數學學習是有順序的,所以數學知識在學生的頭腦中的存儲是有層次、有先后的。為此,非常有必要讓學生對本節課進行適當的回顧與小結,從而使得所學知識秩序井然,使得從本課所學的方法與之前的經驗得以合理的整合。
【研究成果】
在本課的教學中,教師通過引導學生用數學的眼光觀察,讓學生明白可以用面積、數量、長度等將數與形聯系起來,算式可以用正方形、圓形、線段等不同的圖形來展現。這樣的教學落實了三個教學目標。(1)滲透了數學思想方法:學生能用圖形來解決數的問題,能用數的規律來解決圖形的問題。(2)掌握一種方法:讓學生在例題的分析與講解中順利的將數與形進行合理溝通。(3)提升一種能力:學生豐富了自身分析問題的手段與策略,明白數學中的問題并非孤立的,可以從另一個角度來解決問題。
(責編 吳美玲)endprint

