HPM視角下的課堂優化

史瓊怡

摘要： 本文從“橢圓定義”入手剖析教材，發現學生認知“疑點”。借助HPM微課進行教學重構，意在通過數學史滲透發展學生核心素養，使學生學會把握數學本質，達到落實“立德樹人”的教育目標。

關鍵詞： 數學本質;HPM微課;核心素養;優化教學

中圖分類號： G633.6 ? ? ? ? ? ?文獻標識碼： A ?文章編號： 1992-7711（2019）22-056-1

一、反思教材，發現教學難點

橢圓是學生接觸的首個圓錐曲線，因此它的教學起著舉足輕重的示范作用。教材由兩個探究活動引出定義。

活動一：將長繩的兩端固定于同一點，套上鉛筆，拉緊繩子，移動筆尖。

活動二：將長繩的兩端分別固定于兩點，移動筆尖。

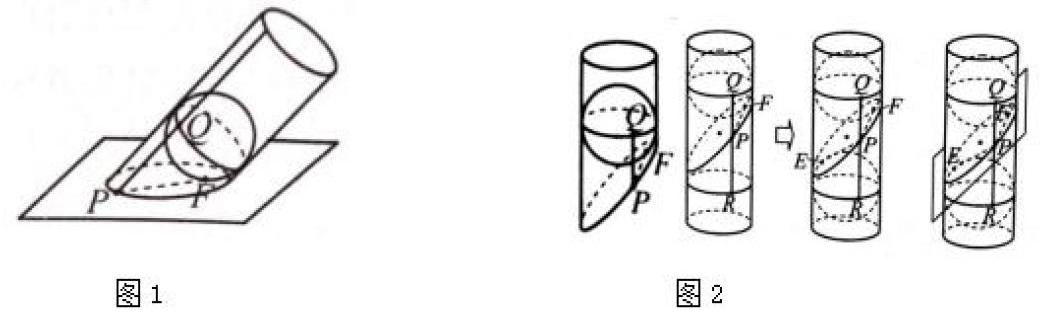
學生通過類比發現橢圓與圓的共性，從而得到軌跡定義。但橢圓的幾何本源——截線定義被置于章頭圖中，荷蘭數學家旦德林發明的雙球模型呈現于課后的“探究與發現”。大多數教師易忽略這兩處幾何素材。學生從生活經驗中已經有了橢圓形狀的表象，能自然地理解截線定義，后經學習又獲得了橢圓代數形式的表象，即軌跡定義。但傳統教學并未將這兩者聯系起來，導致學生認知割裂。旦德林的雙球模型實現了從截線定義到軌跡定義的過渡，是橢圓教學的理想模型。該模型不僅能展現橢圓截線定義又蘊含了軌跡定義，既有幾何直觀又有嚴謹證明，幫助學生填平兩種表象間的鴻溝，深刻理解橢圓內涵。

二、借力微課，重構教學場景

HPM微課選取三個常見情境作為引入：“半杯水”的設計為截線定義鋪墊;“握力器的形變”通過演示圓到橢圓的變換，揭示兩者的聯系;“球的影子”是為引出探究實驗和雙球模型。微課設計了以下環節幫助構造雙球模型：①用幾何畫板模擬平行光照射小球，研究球在地面上的影子，并將平行光線看做一個與球相切的圓柱面，影子的橢圓形輪廓可以看成圓柱面與平面的交線。（圖1）②尋找橢圓輪廓上的點P，光線與球面的切點Q，球與地面切點F之間的關系。③模型豎置，逐步構造雙球模型。（圖2）

三、基于素養，評價教學效果

史寧中先生提出數學教育的終極目標：會用數學眼光觀察現實世界，會用數學思維思考世界，會用數學語言表達世界。“三會”目標正是數學核心素養的具體表現。HPM微課旨在通過數學史滲透教學發展學生核心素養，使學生學會把握數學本質，扎實“四基”，提升“四能”。

1.發展數學抽象素養

數學抽象主要是指從數量與數量關系、圖形與圖形關系中抽象出數學概念及概念之間的關系，從具體中抽象出一般規律和結構，它是形成理性思維的基礎，反映數學本質。微課共進行了五次數學抽象。①通過三個橢圓實物，喚起學生腦海中對橢圓形狀的直觀表象，從而引出截線定義。②抽象實驗過程，將平行光線看做一個與球相切的圓柱面，影子的橢圓形輪廓看成圓柱面與平面的交線。③研究“三點”關系，抽象成數學等式。④進一步抽象構造雙球模型，將原先的不變關系轉化成兩球切點與橢圓上點的關系。⑤發現模型中的定長，將點線關系一般化，得到橢圓的軌跡定義。在一次次抽象中，學生逐漸清晰橢圓的幾何本質，學會用數學的眼光觀察現實世界，培養在生活中用數學思維思考問題的習慣。

2.培育直觀想象素養

直觀想象不等同于“數形結合”，是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解和解決數學問題的過程。主要包括：借助空間認識事物的位置關系、形態變化與運動規律;利用圖形描述、分析數學問題;建立數與形的聯系，構建數學問題直觀模型，探索解決問題的思路。正如數學家克萊因曾說：“當一個數學主題在直觀上變得顯然時，才可以認為研究到頭了。”微課通過以下環節培育直觀想象素養：①展示正對頂圓錐，動畫演示當不同角度的平面截對頂圓錐得到的三類曲線，宏觀上發現三類曲線的聯系，幫助學生構造知識框架。②通過平行光照射小球實驗研究橢圓影子上的點與兩切點間線段關系，并讓點動起來，進一步尋探究不變量，幫助學生順利進行數學抽象。動畫的介入能發展學生幾何直觀和空間想象能力，讓學生在具體情境中感悟數學本質。

在回歸概念本質的同時，這兩節HPM微課還滲透著育人的理念，用實例教學生數學地觀察，數學地思考，滲透著數學美感和精神品質教育。

HPM微課是建立在對課本深入理解基礎上，突出科學性、史實性、人文性、趣味性等特點，優化教學。其教學意義在于：利用數學史的教育價值，賦予數學人文意義，讓學生理解數學本質，最終將其內化為核心素養。數學教師要革新教育理念，大膽創新，將數學史的“料”與微課的“形”相結合，使數學史煥發新活力，為課堂添磚加瓦，助力學生素養提升。

[參考文獻]

[1] 中華人民共和國教育部.普通高中數學課程標準（2017年版）[M].北京：人民教育出版社，2018;3-10.

[2]孫雨琴，婁慧敏，朱哲.HPM視角下高中數學課堂教學的特點初探[J].蘇州：中學數學月刊，2018（11）：45-48.

注：本文是全國教育科學“十三五”規劃2018年度教育部重點課題“基于HPM視角下的高中數學系列微課開發研究”（課題批準號：DCA180419）的階段研究成果。

（作者單位：浙江省寧波市五鄉中學，浙江 寧波 315000）