基于邏輯推理素養(yǎng)下的高中數(shù)學(xué)立體幾何教學(xué)策略探析

徐曉華

[摘 ?要] 邏輯推理是學(xué)生發(fā)現(xiàn)和解決問(wèn)題的重要方式，是學(xué)生構(gòu)建數(shù)學(xué)體系、有邏輯有條理地與其他學(xué)生進(jìn)行交流和討論過(guò)程中所必不可少的能力. 文章以蘇教版高中數(shù)學(xué)“直線與平面垂直的判定”教學(xué)為例，探討了邏輯推理素養(yǎng)視角下高中數(shù)學(xué)立體幾何教學(xué)策略.

[關(guān)鍵詞] 邏輯推理素養(yǎng);高中數(shù)學(xué);立體幾何

作為六大數(shù)學(xué)核心素養(yǎng)之一的邏輯推理素養(yǎng)，意指從一些命題和事實(shí)出發(fā)，充分應(yīng)用歸納、類比等規(guī)則推理出其他命題，它能有效發(fā)展學(xué)生的思維、開(kāi)發(fā)學(xué)生的智力、培養(yǎng)學(xué)生嚴(yán)謹(jǐn)科學(xué)的精神，可以說(shuō)是學(xué)生構(gòu)建數(shù)學(xué)體系、有邏輯有條理地與其他學(xué)生進(jìn)行交流和討論過(guò)程中所必不可少的能力[1]. 而當(dāng)前高中邏輯推理素養(yǎng)的培養(yǎng)并不理想，體現(xiàn)在學(xué)生邏輯推理方面主要為閱讀題目粗心大意，解題邏輯思維混亂，總結(jié)反思、知識(shí)梳理常常流于形式，特別是在高中立體幾何教學(xué)中，所含概念繁多、抽象并且概念與概念之間具有很強(qiáng)的邏輯性. 因此，以高中立體幾何教學(xué)為載體，探究邏輯推理素養(yǎng)下的高中數(shù)學(xué)教學(xué)策略成了增強(qiáng)學(xué)生綜合素質(zhì)、培養(yǎng)學(xué)生創(chuàng)新思維、落實(shí)課程改革“立德樹(shù)人”任務(wù)的關(guān)鍵.

邏輯推理素養(yǎng)下高中數(shù)學(xué)立體幾何教學(xué)策略

1. 注重?cái)?shù)學(xué)概念，牢固樹(shù)立邏輯推理基石

基礎(chǔ)知識(shí)是解決一切問(wèn)題的根基，是進(jìn)行邏輯推理的基石. 針對(duì)當(dāng)前部分高中學(xué)生證明問(wèn)題結(jié)論時(shí)，不能正確應(yīng)用或沒(méi)有意識(shí)應(yīng)用所學(xué)定理和相關(guān)概念的現(xiàn)狀，教師可以讓學(xué)生一開(kāi)始接觸新概念時(shí)，就讓學(xué)生從本質(zhì)上理解它，深度掌握該概念的內(nèi)涵、外延以及可能應(yīng)用之處. 在具體實(shí)踐中，教師可以從一些趣味問(wèn)題或故事情境入手，然后通過(guò)呈現(xiàn)事物的方式有效加深學(xué)生的印象，有效避免學(xué)生死記硬背新概念的現(xiàn)象;并在此基礎(chǔ)上，適當(dāng)加強(qiáng)基礎(chǔ)知識(shí)的變式練習(xí)，從而達(dá)到舉一反三、深度掌握基礎(chǔ)知識(shí)和基本方法的目的.

2. 聚焦問(wèn)題情境，有效創(chuàng)造邏輯推理起點(diǎn)

推理源于問(wèn)題，而問(wèn)題情境的創(chuàng)設(shè)不僅可以引發(fā)學(xué)生產(chǎn)生認(rèn)知沖突，而且還可以促使學(xué)生之間相互交流和溝通，有效創(chuàng)造出邏輯推理的起點(diǎn)[2]. 在具體教學(xué)實(shí)踐中，教師應(yīng)源于數(shù)學(xué)本身，或者從其他學(xué)科汲取，或者從學(xué)生息息相關(guān)的生活出發(fā)創(chuàng)設(shè)問(wèn)題情境，設(shè)置教學(xué)任務(wù)，從而達(dá)到激發(fā)學(xué)生學(xué)習(xí)興趣、引發(fā)學(xué)生思維碰撞的目的.

3. 鼓勵(lì)合情推理，滲透邏輯推理規(guī)則

不難發(fā)現(xiàn)，在情境創(chuàng)設(shè)之后相當(dāng)數(shù)量的學(xué)生會(huì)出現(xiàn)無(wú)從下手的情況，因此教師應(yīng)一改傳統(tǒng)以講授為主的教學(xué)方式，鼓勵(lì)學(xué)生大膽地通過(guò)類比、歸納的方式進(jìn)行猜想，讓學(xué)生敢于將自己的真實(shí)想法表達(dá)出來(lái)，并根據(jù)題目已知條件主動(dòng)地進(jìn)行探究性活動(dòng)，促使學(xué)生在活動(dòng)探究中獲得最為深刻的知識(shí). 值得說(shuō)明的是，在此過(guò)程中教師應(yīng)及時(shí)融入類比和歸納等推理方式，并給予學(xué)生足夠的時(shí)間和自主探索、合作學(xué)習(xí)的空間，有效地促使學(xué)生親身經(jīng)歷合情推理的過(guò)程.

4. 演繹推理驗(yàn)證，示范邏輯推理過(guò)程

合情推理與演繹推理是相互聯(lián)系的，只有經(jīng)過(guò)嚴(yán)格數(shù)學(xué)證明之后的命題才能稱為定理. 因此，在學(xué)生自主探究猜想得出相關(guān)數(shù)學(xué)命題之后，教師還應(yīng)依靠演繹推理的嚴(yán)格論證獲得定理，并在此過(guò)程中不斷強(qiáng)化數(shù)學(xué)邏輯語(yǔ)言的表達(dá)[3]. 在具體實(shí)踐中，為了充分暴露學(xué)生的思維推理過(guò)程和規(guī)范書(shū)寫(xiě)等問(wèn)題，促使學(xué)生加深對(duì)所學(xué)知識(shí)的印象，教師可以先讓學(xué)生嘗試自己的證明，然后呈現(xiàn)嚴(yán)格的證明過(guò)程，從而幫助學(xué)生厘清論證思路，改正自己不良的學(xué)習(xí)習(xí)慣，有效提升學(xué)生的邏輯推理能力.

5. 構(gòu)建知識(shí)體系，梳理邏輯關(guān)系

歸納總結(jié)也是邏輯推理素養(yǎng)下高中數(shù)學(xué)立體幾何教學(xué)中不可或缺的環(huán)節(jié)，因此為了幫助學(xué)生厘清知識(shí)脈絡(luò)，教師還應(yīng)鼓勵(lì)學(xué)生通過(guò)構(gòu)造知識(shí)結(jié)構(gòu)圖的方式將相關(guān)概念、命題以及定理之間的邏輯關(guān)系有條理地呈現(xiàn)出來(lái)，有效提升學(xué)生分析、發(fā)現(xiàn)的邏輯推理能力. 值得一提的是，針對(duì)學(xué)生不會(huì)運(yùn)用概念圖的形式進(jìn)行概括總結(jié)的現(xiàn)狀，教師應(yīng)在課堂教學(xué)中適當(dāng)進(jìn)行示范.

邏輯推理素養(yǎng)下的高中數(shù)學(xué)立體幾何教學(xué)實(shí)踐

僅有相關(guān)理論是不夠的，并且理論與實(shí)踐是相互結(jié)合的. 因此，基于以上邏輯推理素養(yǎng)下高中數(shù)學(xué)立體幾何教學(xué)問(wèn)題情境創(chuàng)設(shè)、知識(shí)體系構(gòu)建等策略，下文以蘇教版高中數(shù)學(xué)“直線與平面垂直的判定”教學(xué)過(guò)程為例進(jìn)行深入探究.

1. 創(chuàng)設(shè)情境，引出定義

為了激發(fā)學(xué)生探究的興趣，培養(yǎng)學(xué)生的愛(ài)國(guó)主義情懷，促使學(xué)生直觀感知直線與平面垂直的本質(zhì)，教師應(yīng)結(jié)合教學(xué)內(nèi)容，及時(shí)利用多媒體播放并介紹日晷這種我國(guó)古代普遍使用的計(jì)時(shí)儀器以及計(jì)時(shí)原理，然后要求學(xué)生逐一思考以下幾個(gè)問(wèn)題：

問(wèn)題1：古代在制作日晷時(shí)，如何能夠準(zhǔn)確判斷晷針與晷盤(pán)垂直.

問(wèn)題2：為了有效解決上述問(wèn)題，如何將日晷計(jì)時(shí)過(guò)程數(shù)學(xué)化.

問(wèn)題3：試著應(yīng)用自己的語(yǔ)言，歸納總結(jié)出直線與平面垂直的定義.

2. 設(shè)置問(wèn)題，得到猜想

為了促使學(xué)生掌握邏輯推理規(guī)則，有效引發(fā)學(xué)生的認(rèn)知沖突，教師應(yīng)根據(jù)線面垂直的定義，推理出若要使得晷針與晷盤(pán)垂直，則需要判斷出晷針與其在晷盤(pán)內(nèi)形成的每一個(gè)影子垂直，顯然這是非常困難的，也是不太現(xiàn)實(shí)的. 于是，為了降低學(xué)生思考的難度，教師應(yīng)采用類比方式，就地取材，要求學(xué)生觀察類似教室內(nèi)暖氣供水管與屋頂面、書(shū)立側(cè)棱與書(shū)立底面之間的特征（如圖1、圖2所示）. 由此引導(dǎo)學(xué)生猜想出若想獲得一條直線與平面垂直，則需要這條直線與該平面內(nèi)的兩條相交直線垂直即可.

3. 操作確認(rèn)，規(guī)范證明

為了有效驗(yàn)證學(xué)生的猜想，幫助學(xué)生在課堂上獲取基本活動(dòng)經(jīng)驗(yàn)，有效強(qiáng)調(diào)猜想中“兩條”“相交”等關(guān)鍵詞語(yǔ)，教師應(yīng)引導(dǎo)學(xué)生通過(guò)如圖3、圖4的方式完成教材中所設(shè)計(jì)的探究活動(dòng)，并思考教材所提出的問(wèn)題.

然后要求學(xué)生應(yīng)用圖形語(yǔ)言和符號(hào)語(yǔ)言表示直線與平面垂直的判定定理，并要求學(xué)生結(jié)合日常實(shí)際列舉生活中直線與平面垂直的實(shí)例. 在此基礎(chǔ)上，為了進(jìn)一步幫助學(xué)生厘清概念和定理之間的邏輯關(guān)系，有效規(guī)范相關(guān)的證明過(guò)程，教師還應(yīng)及時(shí)呈現(xiàn)如下題目，要求學(xué)生先行分析思路并進(jìn)行證明，然后由教師板書(shū)示范過(guò)程.

4. 變式練習(xí)，歸納反思

為了進(jìn)一步加深學(xué)生對(duì)直線與平面垂直判定定理的理解，促使學(xué)生在反思?xì)w納時(shí)有目標(biāo)、有方向，教師還應(yīng)及時(shí)結(jié)合教材例題和相關(guān)的練習(xí)題目，要求學(xué)生獨(dú)立完成如下的變式題目：

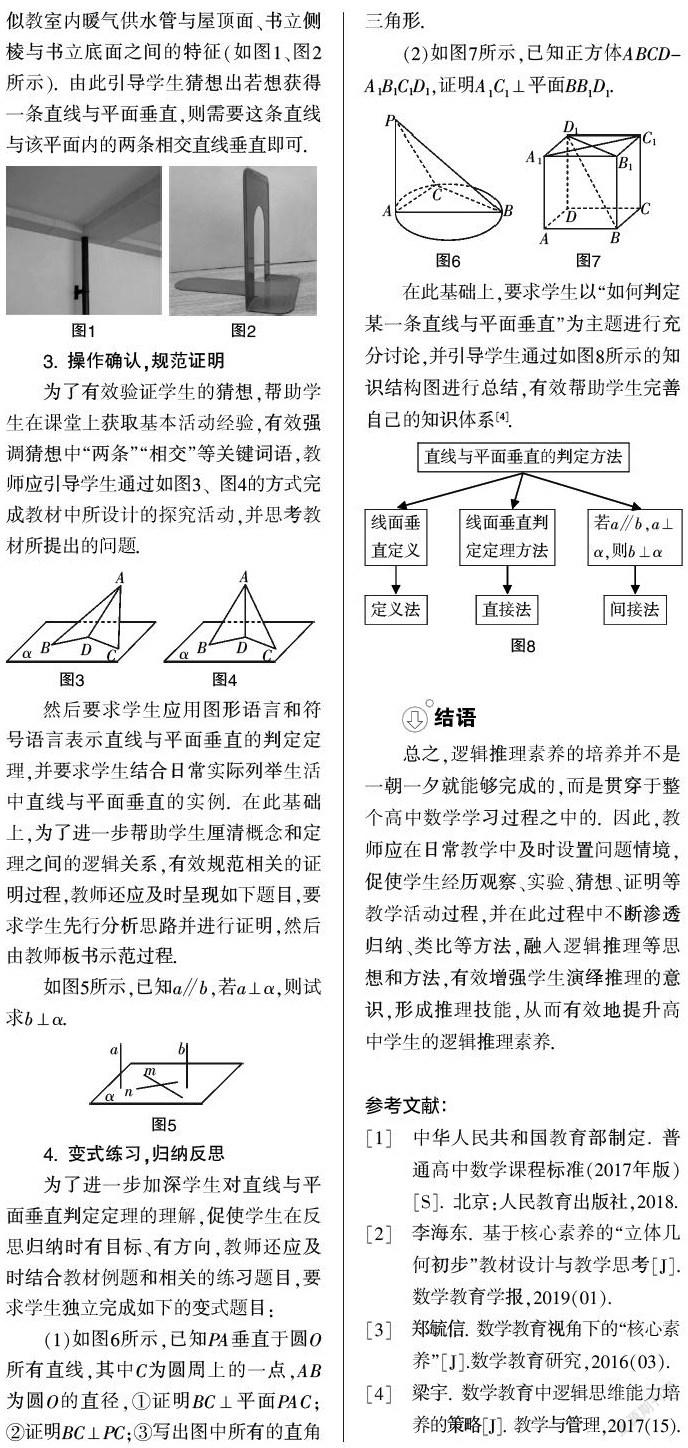
（1）如圖6所示，已知PA垂直于圓O所有直線，其中C為圓周上的一點(diǎn)，AB為圓O的直徑，①證明BC⊥平面PAC;②證明BC⊥PC;③寫(xiě)出圖中所有的直角三角形.

（2）如圖7所示，已知正方體ABCD-A1B1C1D1，證明AC⊥平面BBD.

在此基礎(chǔ)上，要求學(xué)生以“如何判定某一條直線與平面垂直”為主題進(jìn)行充分討論，并引導(dǎo)學(xué)生通過(guò)如圖8所示的知識(shí)結(jié)構(gòu)圖進(jìn)行總結(jié)，有效幫助學(xué)生完善自己的知識(shí)體系[4].

結(jié)語(yǔ)

總之，邏輯推理素養(yǎng)的培養(yǎng)并不是一朝一夕就能夠完成的，而是貫穿于整個(gè)高中數(shù)學(xué)學(xué)習(xí)過(guò)程之中的. 因此，教師應(yīng)在日常教學(xué)中及時(shí)設(shè)置問(wèn)題情境，促使學(xué)生經(jīng)歷觀察、實(shí)驗(yàn)、猜想、證明等教學(xué)活動(dòng)過(guò)程，并在此過(guò)程中不斷滲透歸納、類比等方法，融入邏輯推理等思想和方法，有效增強(qiáng)學(xué)生演繹推理的意識(shí)，形成推理技能，從而有效地提升高中學(xué)生的邏輯推理素養(yǎng).

參考文獻(xiàn)：

[1] ?中華人民共和國(guó)教育部制定. 普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）[S]. 北京：人民教育出版社，2018.

[2] ?李海東. 基于核心素養(yǎng)的“立體幾何初步”教材設(shè)計(jì)與教學(xué)思考[J]. 數(shù)學(xué)教育學(xué)報(bào)，2019（01）.

[3] ?鄭毓信. 數(shù)學(xué)教育視角下的“核心素養(yǎng)”[J].數(shù)學(xué)教育研究，2016（03）.

[4] ?梁宇. 數(shù)學(xué)教育中邏輯思維能力培養(yǎng)的策略[J]. 教學(xué)與管理，2017（15）.