巧用樓層法深入淺出認識正方體堆疊問題的方法探析
張超
摘 要:小學生的空間觀念和空間想象力相對較差,正處于不斷培養和發展的階段,所以在圖形與幾何模塊的學習過程中會比較困難。文章以正方體堆疊問題為例,介紹一種“樓層法”,將正方體類比成樓房,通過數樓層數即可判斷出小正方體個數。這個方法可以幫助學生更好地理解正方體堆疊問題。通過不斷的觀察、分析和想象,逐步在學生的認知里培養空間觀念和想象力,為今后數學的學習打好基礎。
關鍵詞:正方體堆疊;小學數學;空間觀念
正方體堆疊問題在考試題中頻頻出現,空間想象力欠缺的小學生在面對這類題時很難形成空間立體圖形,而教師在教學中多半是讓學生自己去想象,缺少對空間觀念的培養。文章將介紹一種分析方法,即“樓層法”。該方法是通過改變學生觀察的角度,以“排”為單位,從縱向來觀察,在正方體的頂部進行觀察和想象,這種方法不會忽略無法觀察到的正方體,可以準確快速地判斷出堆疊的小正方體的個數,讓學生更好地理解空間圖形,也為教師對學生空間想象力的培養提供了新的方法。
一、 如何使用“樓層法”解決正方體堆疊問題
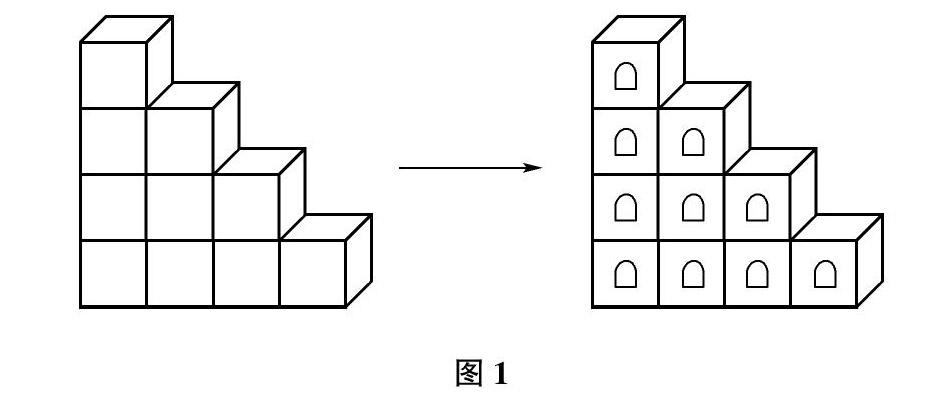
“樓層法”顧名思義,我們將每列的正方體類比成單元樓(圖1),從左邊數起分別為:一單元,二單元,三單元和四單元。每一個單元樓的樓層數是不同的,分別是:4層、3層、2層和1層。那么這個正方體堆疊圖形中含有的小正方體個數就是4+3+2+1=10(個)。這就是用“樓層法”解決正方體堆疊問題。正方體可以類比成樓房,是因為正方體堆疊與蓋房子原理是一樣,正方體堆疊是從下面開始,一個一個小正方體往上堆,而樓房也是同樣的,從最底層開始,一層一層地往上蓋,因此將正方體類比成樓房是非常合理的;此外,樓房在生活中隨處可見,將正方體類比成樓房的方法,與生活實際相結合,學生可以更好地理解立體圖形,有助于空間觀念的培養。
二、 利用“樓層法”求解正方體堆疊問題
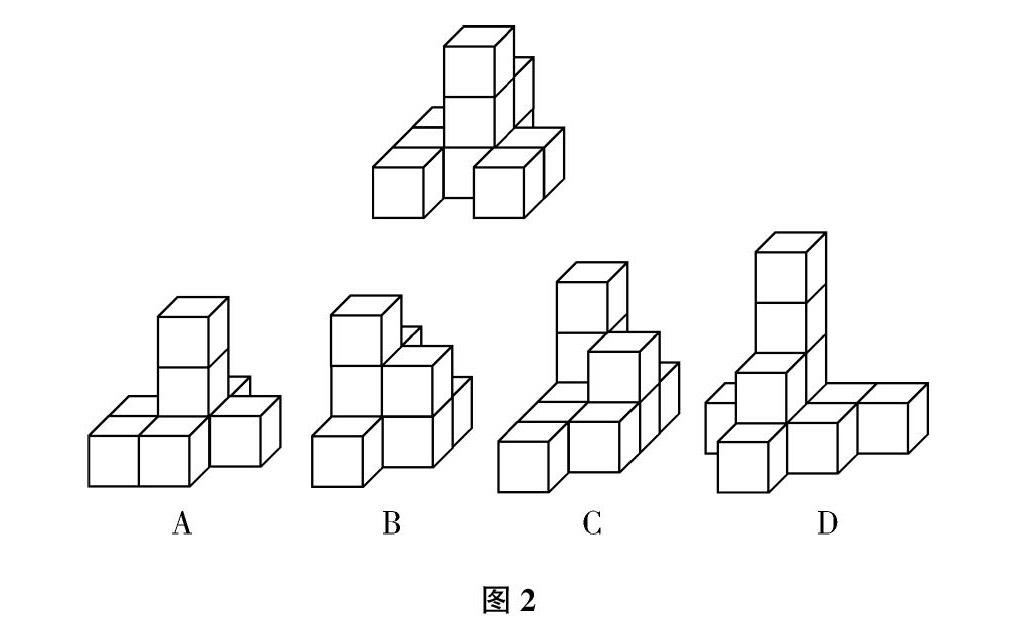
【例1】 如圖2,右側的立體圖中哪個與左側的立體圖中的小正方體個數相同?
解析:左側立體圖中小正方體的個數:左側一排中的每一列都是由1層組成,中間排是有2列組成,每列分別是3層和2層,右側共兩列,每列只有1層,故左側立方體圖中小正方體的個數為:1+1+1+3+2+1+1=10(個)。接下來需要從右側四個圖形中找到由10個小正方體組成的圖形。
選項A:左側中有1+1=2(個),即2個小正方體。中間一排在數層數時要注意,前面是1層,中間是3層,后面還有1層,很多學生可能會將這個小正方體忽略掉。右側只有1層,因此,A選項中小正方體個數有2+1+3+1+1=8(個),與左側圖形數目不同,不符合題意。當我們對于這種方法熟練后,可以直接寫出每列的樓層數,即小正方體個數,直接加和求解。選項B:1+3+2+2+1=9(個)。選項C:1+1+1+3+1+2+1=10(個)。與左側圖形中小正方體個數相同。選項D中小正方體個數為:1+1+2+4+1+1+1=11(個),與題目中的要求不符。因此答案為C。
分析:這一組立體圖較為復雜,有很多隱藏起來的正方形,如果直接去數小正方體個數,很容易丟掉某個小正方體,尤其是選項B,利用“樓層法”完全避免了這種錯誤,只要是在直觀圖中看到的,就可以根據層數數出小正方體的個數。
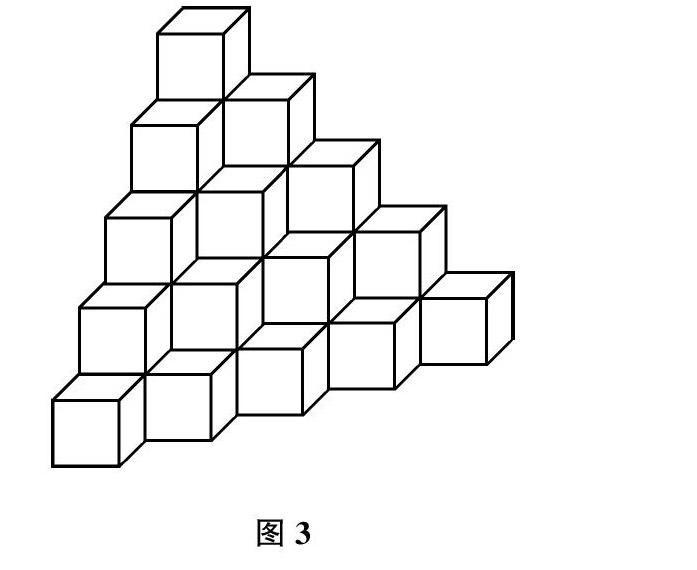
【例2】 圖3中立體圖形至少由??? 個小正方體組成的?
解析:【解法1】利用簡單的“樓層法”數出每一列的小正方體個數。左側一排是由1+2+3+4+5=15(個);第二排:1+2+3+4=10(個);第三排:1+2+3=6(個);第四排有3個,最后一排只有1個。最后將每一排小正方體個數相加:15+10+6+3+1=35(個)。因此,圖3中的立體圖形至少由35個小正方體組成的。
【解法2】利用“分層法”從最高層或者從最底層數起,數出每層含有的小正方體個數,然后加和。仔細觀察發現圖3中的立方體在堆疊時有一定的規律性,即:下層小正方體的個數是在上層正方體的基礎上依次增加2個、3個、4個、5個小正方體。例如:第2層小正方體的個數是在第1層1個正方體的基礎上加上2個小正方體,即1+2=3(個);第3層是在第2層3個的基礎上加上3個小正方體,即1+2+3=6(個);以此類推,第4層小正方體的個數為:1+2+3+4=10(個);第5層小正方體的個數有:1+2+3+4+5=15(個)。最后將每一層的小正方體數加起來為:1+3+6+10+15=35(個)。與解法1的答案相同。
分析:比較兩種解題方法,解法2是先通過觀察和分析發現被壓的小正方體的個數與上一層的小正方體個數相同,每多加一層,小正方體的個數就在上層小正方體的個數的基礎上增加該層的層數個。這種方法需要學生仔細觀察,不僅需要空間思維能力還需要學生的總結歸納和分析能力。而“樓層法”則相對簡單,通過比較樓層的高低,我們能夠清晰地觀察到每一列所含的小正方體的個數,不會因為遮擋和堆疊而漏掉某個小正方體。
拓展:教師在進行解法2的講解時,可以增設一問:如果依規律擺下去,當擺到第10層時,立體圖形是由??? 個小正方體組成的?依照規律,第幾層就是在上一層的基礎上加上該層層數個小正方體,所以第10層的小正方體個數為第9層的小正方體個數加10。即:1+(1+2)+(1+2+3)+(1+2+3+4)+…+(1+2+3+4+5+6+7+8+9+10)=220(個)。這一問的增設,既可以加深學生對解法2的理解,又可以調動學生探究未知的積極性,讓學生更好地融入課堂的學習中。
三、 正方體堆疊與補全正方體的混合求解
【例3】 如圖4所示,要想把下面左邊的立體圖形補全成為右邊的大的完整的正方體,至少還需要多少個小正方體呢?
解析:想要知道還需要多少個小正方體,首先需要確定右側的大正方體(我們將完整的大正方體定義為“整體”)和左側的殘缺的立體圖(我們將殘缺的立體圖定義為“部分”)中含有的小正方體個數,再利用“整體的數量-部分的數量=需要補充的數量”的方法,求解出還需要多少個小正方體。根據“樓層法”可以直接判斷出“部分”圖形中含1+2+3+1+2+2+1+1+1=14(個)小正方體。右側“整體”的立體圖形中總共有3+3+3+3+3+3+3+3+3=27(個)小正方體。因此,根據“整體的數量-部分的數量=需要補充的數量”計算,故至少還需要27-14=13(個)小正方體,可以將左邊的立體圖形補全成為右邊的大的完整的正方體。答案為13個。

