高中數學“數列”單元教學研究

陸江 陳倫全

【摘要】在整體教學視域下，通過構建單元知識的鏈條和結構體系，整體設計單元教學方案，引導學生進行單元整體性和聯系性的學習，有利于發展核心素養。立足區域單元整體，進行單元教學整體設計的區域研究與實踐，探索單元教學整體設計的策略與路徑，在實踐中發展學生的數學核心素養，提升教師的單元教學整體設計的能力。

【關鍵詞】高中數學;數列;單元教學設計

一.數列在高中數學中具有重要地位

數列在高中數學中占有重要的地位，它既是初中數學知識的進一步拓展，又是大學數學課程的基礎，同時對高中數學其他章節的學習有著間接的影響。數列是特殊的函數，對數列的深入研究有助于對函數知識的學習和掌握。

二.揭示數列與相關知識的聯系，構建數列知識團

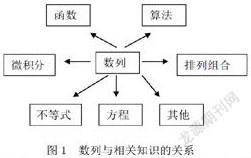
數列與函數、算法、微積分、排列組合、方程、不等式等內容有著密切的聯系，通過對“數列”單元的教學設計研究，可以從宏觀上揭示數列與相關知識的聯系，構建數列知識團。如數列與函數、算法、微積分、方程等的數學知識的內在聯系表現為圖1。

三、高中數學“數列”單元教學設計要素分析

1.數學分析

（1）數列是定義域為正整數集或其子集的特殊函數

數列是離散函數的一種，離散函數是相對于定義在實數集或者實數集的某個子區間上的函數而言的。數列是離散函數的重要數學模型之一，在數學中有著重要的地位。

（2）數列是刻畫實際問題的重要模型

數列本身也是一個數學的研究對象，其中斐波那契數列就是一個非常重要的數學研究對象。

（3）數列的生成體現著遞歸思想

遞歸和類比思想是研究數列的重要的基本思想.

2.課程標準分析

（1）數列的學習突出了函數思想

《課程標準》將數列、等差數列和等比數列都作為一種特殊的函數、作為反映自然規律的基本數學模型來學習，加強了數列與函數的聯系，更注重知識產生的背景和應用。

（2）與“大綱”比較，《課程標準》更關注數列知識的應用

《課程標準》對于數列的概念、通項公式的要求比“大綱”降低了，前者只是了解，后者與列表和圖象是同等地位，沒有單獨提出來。《課程標準》在對等差、等比數列的知識要求上與“大綱”大致相同，只是《課程標準》更關注學生的參與和發現、背景和應用，以及與函數的聯系。

（3）突出過程，強調從特殊到一般

對于等差、等比數列，要從一些具體數列的實例出發，歸納、總結一般等差數列、等比數列的特征。例如，1，2，3，4，5，…， 是典型的等差數列，此數列可以作為等差數列的典型代表，等差數列的特征、前n項和的公式都可以從研究這個具體數列中歸納出來。

四.單元教學目標設計

1.課程目標

本章學習的主要內容是數列的概念和簡單表示法、等差數列與等比數列。數列作為一種特殊的函數，是反映自然規律的基本數學模型，本章強調用函數的背景和研究方法來認識數列、研究數列，教學中應力求通過實際問題引入數列概念后，使學生體會數列的函數背景，感受數列是研究現實問題情境的數學模型。

2.學習目標

（1）數列的概念和簡單表示法

通過日常生活中的實例，了解數列的概念和幾種簡單的表示方法（列表、圖象、通項公式），了解數列是一種特殊函數。

（2）等差數列、等比數列

通過實例，理解等差數列、等比數列的概念，探索并掌握等差數列、等比數列的通項公式與前n項和的公式，能在具體的問題情境中，發現數列的等差關系或等比關系，并能用有關知識解決相應的問題，體會等差數列、等比數列與一次函數、指數函數的關系。

五.單元教學重點設計

本章的重點有兩個：一是數列的概念和性質;二是利用數列的相關知識解決實際問題，尤其是生活中的經濟問題。

數列的概念和性質的學習，要突出函數的本質，等差數列是線性函數的離散化;等比數列是指數函數的離散化，可以利用函數的性質來理解和認識數列的性質。在我們的實際生活中，一般情況下按月、按年表述的問題，如利率、增長率等，抽象出來的數學問題就是數列的應用。

六.單元教學流程設計

本章教學流程圖：

圖2 數列單元教學流程圖

七.教學建議與實施

研究發現，第一，就單元教學目標看，應使學生體會數列的函數背景，感受數列是研究現實問題情境的數學模型，感受等差數列和等比數列模型的廣泛應用，并能利用它們解決一些實際問題。第二，對單元框架設計而言，要將數列的教學看成一個整體。首先對數列從概念辨析、本質理解、通項公式、遞推公式等四個方面進行學習，然后依據由特殊到一般的研究思路對等差數列和等比數列進行學習，從而體現出數列單元的有機整體性。第三，在數列單元的具體教學過程中，應注意整體把握教材、注重數學思想和數學方法的形成、關注學生的主動參與和知識的發生發展過程等方面。故在數列單元的教學過程中，應該努力做好一些幾個方面：

1.整體把握教材

站在全局的角度，以知識單元的觀點審視數列內容，可以將數列的學習進行科學的整合。首先，可以從數列的概念生成，函數本質，通項公式，遞推關系等視角對數列做一基本的處理和學習，而后可以擴展到數列的前n項和求解，并可以探索前n項和與數列的第n項之間的關系，形成和項互化公式。其次，本章的學習可以從特殊到一般進行，先對數列有一個基本的認識和了解，進而利用等差數列和等比數列兩類特殊的數列對數列進行詳實的研究。

2.注重數學思想和數學方法的形成

等差數列和等比數列始終是一對孿生兄弟，對二者的學習往往可以借助于類比的思想方法，只要學生對等差數列有比較好的掌握和理解，對等比數列的學習將可以完全類比等差數列學習的思路進行。

參考文獻

[1] 高洪菊. 高中數列教學設計研究[D]. 長春： 東北師范大學，2010。

[2] 韓相河. 《數列》的教學設計[J]. 中學數學雜志，2008（07）：16-19.