“好問題”與“好課堂”
李建梅
[摘 要]數學是抽象的,并具有高度概括的特征。如何讓純粹的數學轉化為兒童可接受的童化數學,離不開教師對兒童認知過程的深入分析,對問題的精心預設。基于本質、驅動思維、指向素養(yǎng)的問題,才是好問題。在具有統攝功能的核心問題驅動下,引領兒童思維攀高,驅動課堂向縱深進發(fā)。
[關鍵詞]核心問題 數學本質 學科素養(yǎng)
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2016)05-010
【課前思考】
一、認識長方形和正方形應經歷怎樣的學習過程?
學生在一年級上學期學習了立體圖形之后,下學期便開始正式接觸長方形和正方形。正式接觸長方形和正方形之前,學生對它們的認識還停留在直觀感知層面:會找尋,能識別,在釘子板上圍,利用方格紙畫……缺乏對長方形和正方形本質特征的關注。三年級的學習便提出了對長方形和正方形的特征進行抽象概括的要求,而如何在喚醒學生感性經驗的同時加強對邊和角的關注是本節(jié)課的難點,引導學生從對個別圖形的研究轉到用更多圖形進行驗證,實現感知到思維的提升則是本節(jié)課的重點。
二、怎樣的核心問題能驅動整個學習活動?
問一年級的學生:“長方形、正方形長什么樣?”他們會有各種各樣的表達方式:畫個草圖,拿個實物,蓋個印章……直觀形象、簡單明了地詮釋自己的理解。三年級學生研究的“長方形和正方形的特征”不過是對“長方形、正方形長什么樣”更為理性的表達。對于還處于從直觀形象思維向抽象形象思維過渡的三年級學生而言,筆者認為用“長方形、正方形長什么樣”的這個核心問題來驅動本節(jié)課的學習是適宜的,它不僅通俗易懂,直抵本質,而且可以實現對前后兩個階段不同水平學習的整體觀照。
【教學規(guī)劃】
一、在直觀操作中聚焦邊與角的特征
核心問題:長方形、正方形長什么樣,你會表示嗎?
1.畫一畫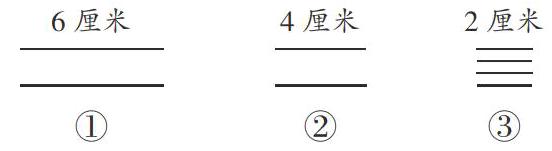
(1)談話:今天我們研究的內容是“長方形和正方形”(板書:長方形和正方形),在你的腦海里“長方形、正方形長什么樣?”不妨選擇一個把它畫下來。(學生自己選擇是在練習紙的空白處、橫線上還是方格上畫)
(2)思考:你們選擇在哪里畫長方形或正方形?為什么?
(3)小結:大家在畫長方形或正方形的時候已經留意到邊(板書:邊)是直直的,這是它們的一個重要特征。
【思考:“你們選擇在哪里畫長方形或正方形,為什么?”看似不經意卻是關鍵性的一問,觸動了學生敏感的神經,通過在“選地方畫圖”的分析中意識到橫線比空白好,方格為最好,從而引發(fā)學生對長方形、正方形邊和角的關注,將以往學生無意識的行為轉化為有意義的學習活動。】
2.擺一擺
(1)談話:我們不但能畫出長方形、正方形,我們應該還能用小棒擺出這兩種圖形。如果給大家提供以下3種規(guī)格的小棒,你能擺出長方形或正方形嗎?
(2)在學生選擇前設問:如果擺長方形你打算選擇怎樣的小棒?
(3)在學生操作時追問:長棒和短棒恰好組成角“ ”時,我們看到這位同學把短棒進行了一次調整,他在調整什么?想調整成什么角?(教師及時用三角尺上的直角進行比較)
(4)小結:看來擺長方形或正方形時,我們不僅要關注邊,還要關注角。(板書:角)
(5)讓學生在大腦中構圖,說出其他擺法。
【思考:“如果擺長方形你打算選擇怎樣的小棒”強化學生對長方形對邊相等的感知,對學生操作過程中出現的必然現象進行追問:“他在調整什么?想調整成什么角?”喚醒了學生的潛意識,很自然地引發(fā)學生對長方形的角的關注。】
3.比一比
這幾個長方形的邊和角有什么共同的地方?正方形呢?(板書:對邊相等 四條邊相等 四個都是直角)
【思考:用3種不同規(guī)格的小棒擺一擺,既是一次思維的開放,也是將相似結構的圖形進行歸納比較的重要素材。“這幾個長方形的邊和角有什么共同的地方?”再次帶學生回歸到對圖形本質特征的關注上。】
二、在操作驗證中概括邊與角的特點
核心問題:長方形、正方形長什么樣,你會研究嗎?
1.談話與設問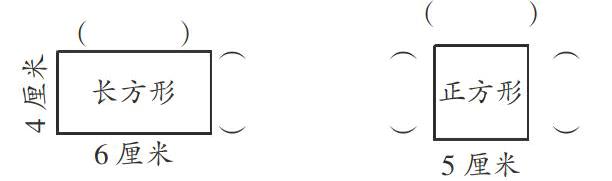
應該說“四個角都是直角,對邊相等”是這3個長方形的特征,“四條邊相等”是這幾個正方形的特征。是不是所有的長方形和正方形都有這樣的特點?(板書:?)我們還需要進行怎樣的研究?
2.操作驗證
(1)談話與設問:為了研究的方便,老師給你們每個小組(4人一組)準備了一個信封,信封里裝著大大小小的2個長方形和2個正方形。每個人選擇其中一個圖形試著驗證給小組的其他成員看。你打算如何進行驗證?
(2)研究操作導圖:從下面這幅連環(huán)畫你能否看懂如何“量一量、折一折、比一比”?

